第十六章：目标规划

16.1 目标规划的数学模型

16.1.1 概念

• 正、负偏差变量
• 绝对（刚性）约束和目标约束
• 优先因子（优先等级）与权系数
• 目标规划的目标函数

16.1.2 一般数学模型

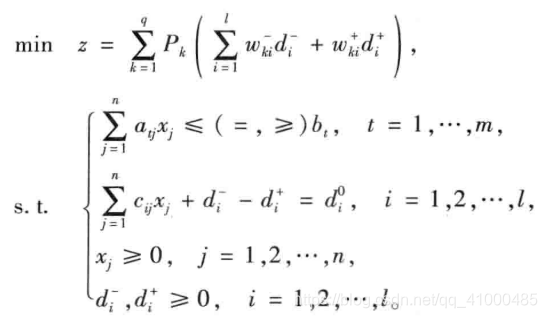
16.2 求解目标规划的序贯算法

根据优先级的先后次序，将目标规划问题分解成一系列的单目标规划问题，然后再依次求解。
需要用到Lingo程序。

16.3 多目标规划的Matlab解法

使用fgoalattain函数
M函数

function F=Fun(x);
F=[-100*x(1)-90*x(2)-80*x(2)-70*x(4)
3*x(2)+2*x(4)];

a=[-1 -1  0  0
   0  0  -1 -1
   3  0   2  0
   0  3   0  2];
b=[-30 -30 120 48]';
c1=[-100 -90 -80 -70];
c2=[0 3 0 2];
[x1,g1]=linprog(c1,a,b,[],[],zeros(4,1))  
[x2,g2]=linprog(c2,a,b,[],[],zeros(4,1))  
g3=[g1;g2];  
[x,fval]=fgoalattain('Fun',rand(4,1),g3,abs(g3),a,b,[],[],zeros(4,1))
%这里权重weight=目标goal的绝对值

可能每次运行的结果都是不一样的，不过差异不大
下面使用匿名函数求解：

clc,clear
a=[-1 -1  0  0
   0  0  -1 -1
   3  0   2  0
   0  3   0  2];
b=[-30 -30 120 48]';
c1=[-100 -90 -80 -70];
c2=[0 3 0 2];
fun=@(x) [c1;c2]*x;  
[x1,g1]=linprog(c1,a,b,[],[],zeros(4,1))  
[x2,g2]=linprog(c2,a,b,[],[],zeros(4,1))  
g3=[g1;g2]; 
[x,fval]=fgoalattain(fun,rand(4,1),g3,abs(g3),a,b,[],[],zeros(4,1))

16.4 目标规划模型的实例

均需使用Lingo软件实现，由于对其不熟悉，此处便不予详解。