VLSI数字信号处理系统——第八章快速卷积

VLSI数字信号处理系统——第八章快速卷积

作者：夏风喃喃
参考：
(1) VLSI数字信号处理系统:设计与实现 （美）Keshab K.Parhi／著
(2) socvista https://wenku.baidu.com/u/socvista?from=wenku

一.引言

卷积是数字信号处理中最常见也是最重要的计算之一。利用卷积可以实现相关计算和 FIR 滤波等等。这里我们重点讨论快速卷积，快速卷积对卷积速度要求较高。在保证速度的前提下，尽可能使用简单运算（加法）来代替复杂运算（乘法），同时还有利于计算共享，从而节约面积，与此同时功耗也能得到一定程度的改善。

考虑如下复数乘法，(a + jb)是样值信号，(c + jd)是系数。

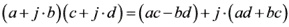
将其写成矩阵形式，有

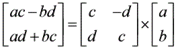
从矩阵式中，可以看出一对复数相乘，需要 4 次乘法和 2 次加法。相同的功能，如果采用下面的计算过程

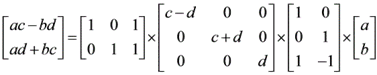
新的矩阵计算方式只需要 3 次乘法 3 次加法。第一个矩阵2次加法，第二个矩阵3次乘法，第三个矩阵1次加法。从应用角度说，因为是固定系数，c - d 和 c + d 所涉及的两次加法是不占计算量的。

实际上卷积有三种表示，

1. 求和形式
   
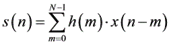
2. 矩阵形式（有限长序列卷积）
   如2×2卷积：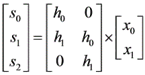
   如2×3卷积：
   
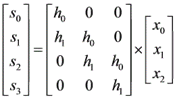
3. 多项式相乘形式（频域相乘）
   

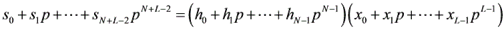
快速卷积算法，就是以卷积的多项式表示来进行构造的。

本章给出了设计快速卷积算法的两种著名方法。第二节讨论了基于拉格朗日插值的Cook-Toom算法，用于小尺寸的线性卷积。第三节讨论了基于中国剩余定理(CRT)的Winograd算法，用于尺寸稍大的线性卷积和循环卷积。第四节阐述了用短卷积算法导出长序列卷积的高计算效率的实现形式。第五节讨论了环形卷积及其与线性卷积的关系。第六节讲述了通过观察来设计快速卷积算法。

二.Cook-Toom算法

2.1 拉格朗日插值定理

设${\beta }_0，{\beta }_1，\dots \dots ，{\beta }_n$为[a, b]上 n+1 个互不相同的点。如果在点 ${\beta }_i$（i = 0，1，……，n）处的函数值$S_i$已知，则存在唯一的次数不高于 n 的多项式$S(p)$使得$S(p){|}_{p={\beta }_i}=S_i$ ，该多项式有下式给出

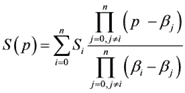
2.2 卷积和拉格朗日插值的关系

卷积可以表示成多项式乘法，考虑 线性卷积，其中

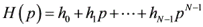
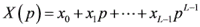
卷积结果就是

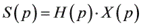
中的

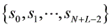
Cook-Toom 算法所要做的就是利用拉格朗日插值公式，导出$S(p)$的符号式。

2.3 Cook-Toom算法

1. 选择 L+N-1 个不同的实数 ${\beta }_0，{\beta }_1，\dots \dots ，{\beta }_{L+N-2}$，一般是选择整数，如0，±1，±2，±3等，不同的取值将会导致不同的快速卷积结果。
2. 计算$H({\beta }_i)$和$X({\beta }_i)$，i = 0,1，……，L+N-2。
3. 计算$S({\beta }_i)=H({\beta }_i)X({\beta }_i)$，i = 0,1，……，L+N-2。
4. 用拉格朗日插值公式，算出$S(p)$的符号式。

Cook-Toom算法可以理解为矩阵的分解。通常，卷积可以表示为矩阵形式

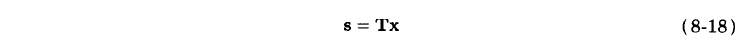
Cook-Toom算法将其分解为

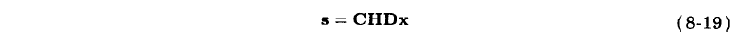
其中，C是后置加法矩阵，D是前置加法矩阵，H是主对角线元素为$H_i$的对角线矩阵。通用乘法的数目完全由对角线矩阵H的非零对角元素的数目来确定。

2.4 修改后的Cook-Toom算法

1. 选择L+N-2个不同的实数${\beta }_0，{\beta }_1，\dots \dots ，{\beta }_{L+N-3}$，一般是选择整数，如0，±1，±2，±3等，不同的取值将会导致不同的快速卷积结果。
2. 计算$H({\beta }_i)$和$X({\beta }_i)$，i = 0,1，……，L+N-3。
3. 计算$S({\beta }_i)=H({\beta }_i)X({\beta }_i)$，i = 0,1，……，L+N-3。
4. 计算$S^{\prime }({\beta }_i)=S({\beta }_i)-S_{L+N-2}{p}^{L+N-2}$，i = 0,1，……，L+N-3。
5. 用拉格朗日插值公式，算出$S^{\prime }(p)$的符号式。
6. 计算$S(p)=S^{\prime }(p)+S_{L+N-2}{p}^{L+N-2}$

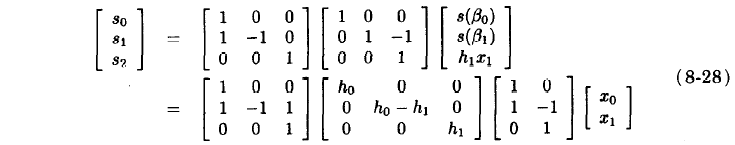
三.Winograd算法

3.1 中国剩余定理

Winograd短卷积算法基于中国剩余定理(CRT)，它的描述如下：

CRT：如果已知一个非负整数在给定的不同模数下对应的余数，若这些模数互素并且已知该整数小于这些模数之积，则该非负整数可唯一确定。

整数CRT：已知$c_i=cmod{m}_i$，i=0,1,…,K-1，其中$m_i$为互素的模数，又令$M={\sum }_{i=0}^{K-1}{m}_i$，$M_i=M/m_i$，求解$N_i{M}_i+n_i{m}_i=GCD(M_i,m_i)=1$得$N_i$。则有$$c=(\sum _{i=0}^{K-1}{c}_i{N}_i{M}_i)modM$$
例:使用整数CRT求解孙子算经中的 “今有物，不知其数，三三数之，剩二；五五数之，剩三；七七数之，剩二。问物几何？”
原题数学表示为$m_0=3，m_1=5，m_2=7$，且有$$c_0=cmod3=2$$$$c_1=cmod5=3$$$$c_2=cmod7=2$$
又因为$M={\sum }_{i=0}^{K-1}{m}_i=3\times 5\times 7=105$，所以$$M_0=105mod3=35$$$$M_1=105mod5=21$$$$M_2=105mod7=15$$
由最大公因数公式，求解$N_i$得：$$-35+12\times 3=1，N_0=-1$$$$21-4\times 5=1，N_1=1$$$$15-2\times 7=1，N_2=1$$
最终c计算如下$$c=(\sum _{i=0}^{K-1}{c}_i{N}_i{M}_i)modM=(2\times (-1)\times 35+3\times 1\times 21+2\times 1\times 15)mod105=23$$

多项式CRT：

3.2 Winograd算法

1. 选择K个互素的实系数多项式$m_i(p)$，其中$i=0,1，\dots ，K-1$，并使得$M(p)={\sum }_{i=0}^{K-1}{m}_i(p)$阶数大于$S(p)=H(p)X(p)$阶数。
2. 令$M_i(p)=M(p)/m_i(p)$，并利用欧几里德GCD算法求解公式$N_i(p)M_i(p)+n_i(p)m_i(p)=GCD(M_i(p),m_i(p))=1$得$N_i(p)$。
3. 计算余数式$S_i(p)=(H_i(p)X_i(p))mod{m}_i(p)$，其中$H_i(p)=H(p)mod{m}_i(p)$且$X_i(p)=X(p)mod{m}_i(p)$。
4. 用CRT公式(公式8-42)，计算$S(p)$。

例：

3.3 修改后的Winograd算法

1. 选择K个互素的实系数多项式$m_i(p)$，其中$i=0,1，\dots ，K-1$，并使得$M(p)={\sum }_{i=0}^{K-1}{m}_i(p)$阶数等于$S(p)=H(p)X(p)$阶数（保证$M(p)$最高次系数为1）。
2. 令$M_i(p)=M(p)/m_i(p)$，并利用欧几里德GCD算法求解公式$N_i(p)M_i(p)+n_i(p)m_i(p)=GCD(M_i(p),m_i(p))=1$得$N_i(p)$。
3. 计算余数式$S_i^{\prime }(p)=(H_i(p)X_i(p))mod{m}_i(p)$，其中$H_i(p)=H(p)mod{m}_i(p)$且$X_i(p)=X(p)mod{m}_i(p)$。
4. 用CRT公式(公式8-42)，计算$S^{\prime }(p)$。
5. 计算$S(p)=S^{\prime }(p)+h_{N-1}{x}_{L-1}M(p)$

例：

四.迭代卷积

1. 将长卷积分解为若干级短卷积。
2. 构建短卷积的快速卷积算法。
3. 用短卷积算法迭代(层次)实现长卷积。

例：

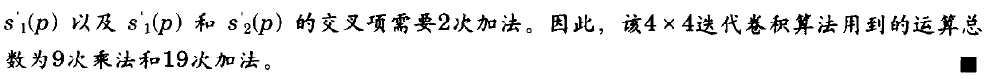
五.循环卷积

循环卷积又称为环形卷积。循环卷积也可以用Winograd算法构造，但N点循环卷积的$M(p)=p^N-1$，而不能任意规定。N点循环卷积，有如下关系$$S(p)=H(p)X(p)modM(p)$$

例：

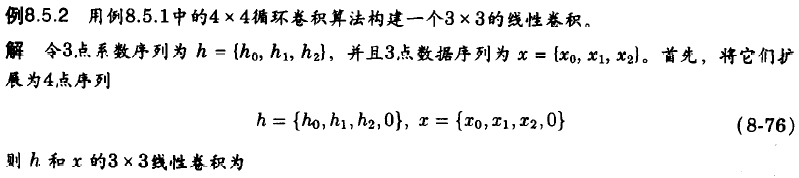
六.通过观察设计快速卷积算法

不是所有的高效卷积算法都可以由Cook-Toom或Winograd算法生成。通过观察也可以生成一个更好的算法。

例：

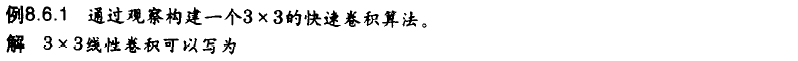
七.结论

本章介绍了各种短快速卷积算法，包括Cook-Toom算法、改进的Cook-Toom算法、Winograd算法、改进的Winograd算法。基于这些快速短卷积算法，可以通过迭代卷积方法得到长卷积算法。循环卷积与线性卷积关系及互相导出。快速卷积算法构成了快速并行FIR滤波器设计的基础。