【AVL模板题】PTA甲级1066 Root of AVL Tree

1066 Root of AVL Tree

https://pintia.cn/problem-sets/994805342720868352/problems/994805404939173888

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

 

 

 

 

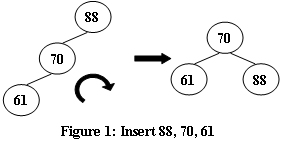
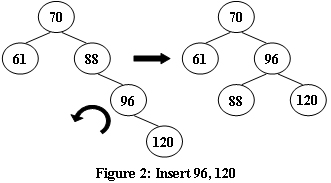
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

 

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

70

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

88

//AVL旋转， 输出按序建成AVL树后的根节点
//本题只有最多20个节点，但其实100000也可以过
//AVL一共四种旋转，稳定保持该树在logn层
#include <bits/stdc++.h>
using namespace std;

struct node
{
    int h,l,r,val;  //该节点的高度，左节点编号，右节点编号，值
}a[100];
int cnt;

int height(int k)  //返回该节点的高度，-1表示此节点为空，故返回0
{
    if(k==-1) return 0;
    else return a[k].h;
}

int turn_LL(int k1)  //左旋。应用于插入在左子树的左节点
{
    int k2=a[k1].l;
    a[k1].l=a[k2].r;
    a[k2].r=k1;
    a[k1].h=max(height(a[k1].l),height(a[k1].r))+1;  //更新高度
    a[k2].h=max(height(a[k2].l),a[k1].h)+1;
    return k2;
}

int turn_RR(int k1)  //右旋。应用于插入在右子树的右节点
{
    int k2=a[k1].r;
    a[k1].r=a[k2].l;
    a[k2].l=k1;
    a[k1].h=max(height(a[k1].l),height(a[k1].r))+1;
    a[k2].h=max(height(a[k2].r),a[k1].h)+1;
    return k2;
}

int turn_LR(int k1)  //先左旋再右旋。应用于插入在左子树的右节点
{
    a[k1].l=turn_RR(a[k1].l);
    int root=turn_LL(k1);
    return root;
}

int turn_RL(int k1)  //先右旋再左旋。应用于插入在右子树的左节点
{
    a[k1].r=turn_LL(a[k1].r);
    int root=turn_RR(k1);
    return root;
}

int Insert(int val,int root)
{
    if(root==-1)  //插入节点
    {
        a[cnt].l=a[cnt].r=-1;  //阔出它左右节点
        a[cnt].val=val;
        a[cnt].h=1;
        root=cnt; //此节点标为cnt
        cnt++;  //cnt++，下一次就是下一号节点
    }

    else if(val<a[root].val)
    {
        a[root].l=Insert(val,a[root].l);  //如果要插入root节点的左子树，就递归
        int left=a[root].l;
        int right=a[root].r;
        if(height(left)-height(right)==2) //要是打破AVL平衡，高度差>=2，就旋转
        {
            if(val<a[left].val) //插在左左
            {
                root=turn_LL(root);
            }
            else   //插在左右
            {
                root=turn_LR(root);
            }
        }
    }

    else
    {
        a[root].r=Insert(val,a[root].r);
        int left=a[root].l;
        int right=a[root].r;
        if(height(right)-height(left)==2)
        {
            if(val>a[right].val)
            {
                root=turn_RR(root);
            }
            else
            {
                root=turn_RL(root);
            }
        }
    }

    a[root].h=max(height(a[root].l),height(a[root].r))+1;   //更新根节点高度
    return root;
}

int main()
{
    int root=-1,cnt=0;
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;i++)
    {
        int x;
        scanf("%d",&x);
        root=Insert(x,root);
    }
    printf("%d\n",a[root].val);
}