密码篇——非对称加密

目录

非对称密码介绍

公钥通信流程：

公钥密码无法解决的问题：

公钥密码算法：

针对RSA的攻击

其他公钥密码：

总结：

---

非对称密码介绍

在对称加密中，加密与解密使用的密钥是相同的，因此必须向接收者配送密钥。用于解密的密钥必须配送给接收者，由此产生了密钥配送问题。

密钥配送问题：对一份文件进行加密后发送给接收方，接收方需要查看文件就要用密钥解开加密文件才能查看原文件。所以不发送密钥，接收方无法接收文件，发送密钥后，又会被截取，让第三方知道文件内容

解决密钥配送问题可使用公钥密码

公钥密码中，密钥可分为加密密钥和解密密钥。发送者使用加密密钥对消息进行加密，接受者用解密密钥进行解密

由此可得：

1）发送者只使用加密密钥

2）接收者只是用解密密钥

3）解密密钥不可被第三方获取

4）加秘密钥无所谓

 

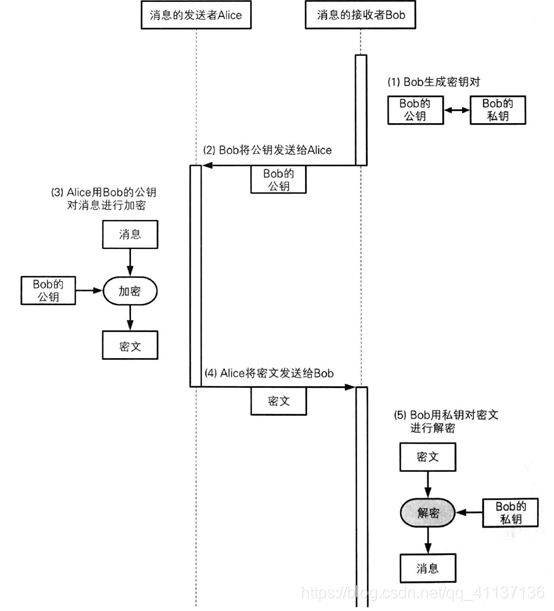
公钥通信流程：

1）接收方生成一个包含公钥和私钥的密钥对

2）接收方将私钥自行保存，并将公钥发送给发送方

3）发送方使用该公钥对消息进行加密后发送（是用公钥只能对数据进行加密，无法解密）

4）接收方使用私钥对密文进行解密

 

注：公钥密码也称为非对称加密。在对称密码中，加密和解密使用的是同一密钥，只是进行相反运算；而非对称加密中，加密与解密使用的是不同密钥，并非对称

两个密钥之间存在着相互依存关系：即用其中任一个密钥加密的信息只能用另一个密钥进行解密

 

公钥密码无法解决的问题：

1）公钥认证问题（需要判断得到的公钥是否合法）

2）处理速度（处理速度只有对称密码的几百分之一）

公钥密码算法：

RSA加密公式：密文 = 明文 E mod N（对代表明文代表的数字E次方除于N求余数，E和N的组合就是公钥）

RSA解密公式：明文 = 密文 D mod N （D和N的组合为私钥）

 

注：N是公开的，所以用于加密和解密的只有E和D

 

为了生成密钥对：需要求得N、L(仅在生成密钥对的过程中使用的数)、E、D

1）求N

使用伪随机数生成器生成两个很大的质数p、q质数：在大于1的自然数中，除了1和它本身不会有其他因数）N=p*q

2）求L

L只出现在生成密钥对的过程中，不会出现于加解密中

L=lcm（p-1,q-1）L是p-1和q-1的最小公倍数

3）求E

1<E<L，gcd（E，L）=1，E与L的最大公约数为1；使用伪随机数生成器生成E的候选数，再判断是否满足最大公约数为1（使用辗转相除法）

4）求D

D是由E得到

1<D<L，E*DmodL=1

 

针对RSA的攻击

中间人攻击：

 

该方法不止针对RSA，可以针对任何公钥密码，因此需要认证公钥是否来自接收方

 

其他公钥密码：

1）EIGamal

经过加密的密文会变成明文的两倍长；该算法是利用modN下求离散对数的难度

2）Rabin

利用modN下求平方根的难度，

3）椭圆曲线密码

密钥长度短于RSA，利用椭圆曲线上的特定点进行特定的乘法运算

 

总结：

1）密码的机密性是通过密钥的长度进行比较的，而非公钥密码强于对称密码

2）公钥密码与对称密码的密钥长度不能直接比较

3）公钥密码并不适合对很长的密码进行加密，现在一般使用的是混合密码（公钥密码和对称密码组合使用：对称密码提高处理速度，公钥密码解决密钥配送问题）

4）RSA中使用的质数数量很多不用担心使用完，和生成密钥对时撞车；且RSA在生成、加密、解密都不需要质因数分解，但在破译RSA时需要使用质因数分解（求p和q）