北方J市长输供热项目以Keras DNN+粒子群优化算法实现当前供热工况下,全网泵组频率预测,及实时优化调控,以实现全网泵组电流最低,进而达到全网能耗最低。本文记录了2024年11月,本人将项目旧算法替换为深度强化学习的DDPG,并使用2024~2025供热季J市真实供热数据进行了验证。
本项目基于DDPG官方团队公开的开源项目并在PyCharm上调试通过,DDPG原版代码详见:
https://gitcode.com/gh_mirrors/ddp/DDPG/blob/main/DDPG.py
1、业务背景知识
长输供热是指将市区外远端热源厂供暖热水通过供水管道引入城市,在千家万户流动后,再通过回水管道流回热源厂重新加温。为了克服水流阻力,在沿途设立若干中继泵站,泵站中的供水管道使用供水加压泵对水流进行加压,回水管道则使用回水加压泵。
为了降低全长输管网运行能耗,收集底层DCS系统全部工况数据,将加压泵频率参数看做可调整参数,其余为不可调整参数。首先计算全部不可调整参数相对于总电流的相关系数,保留相关性高者作为DDPG模型输入参数,输出参数为两组,一组为当前工况下最优频率值,另一组为未来一段时间内平均最低电流值的预测值。
J市长输供热管网总长33公里,沿途共设有6个中继泵站,全部中继泵站中共有两组供水加压泵,每组由5台泵组成;四组回水加压泵,每组同样由5台泵组成,即J市长输管网总共有六组泵,共有加压泵30台。
调控目标是:在当前工况(不可调整参数)下,如何调整泵组频率,使得全部30台泵总电流最低。
业务约束为:
·一组5台泵不必全部开启,但只要开启了,则组内各已开泵的频率应基本相同,否则会引发事故。
·已开启泵的频率必须在[30,50]之间。
·电流不应降低过多,一般不超过10%。
2、数据读取
在边缘端数据已被清洗,首先通过接口导入天气历史数据,如下:

具体解释为:

去掉列‘天气现象’、‘天气图片代码’、‘星期几’、‘城市编号’,将汉字标签替换为整数,将UTC时间转换为标准时间格式“%Y-%m-%d %H:00:00”。
raw_temp = pd.read_csv('datasets/weather_new.csv', encoding="utf-8") # 天气历史数据
# 去掉 天气现象、天气图片代码、星期几、城市编号
raw_temp.drop(['id', 'time', 'wea', 'wea_img', 'day_of_week', 'wind', 'cityid'], axis=1, inplace=True)
raw_temp['time_utc'] = raw_temp['time_utc'].apply(lambda x: datetime.fromtimestamp(x))
读入工况原始数据,并将时间戳的分和秒部分清零,相同行只保留一行,将工况数据变为间隔一小时一条记录。
# 工况原始数据预处理
raw_data = pd.read_csv('datasets/data_2025_1.csv', encoding="utf-8") # 石热24年新数据
raw_taginfo = pd.read_csv('datasets/taginfo.csv', encoding="gbk") # 石热测点信息
# 将原始数据采集时间的分钟和秒清零
raw_data['timestamp'] = raw_data['timestamp'].astype('string')
# 定义替换条件和值
def replace_values(row):
# 将时间戳转换为 datetime 对象
dt_object = datetime.utcfromtimestamp(int(row['timestamp']))
row['timestamp'] = dt_object.strftime('%Y-%m-%d %H:00:00')
# row['timestamp']=tmp_temp.replace(minute=0, second=0)
return row
raw_data = raw_data.apply(replace_values, axis=1)
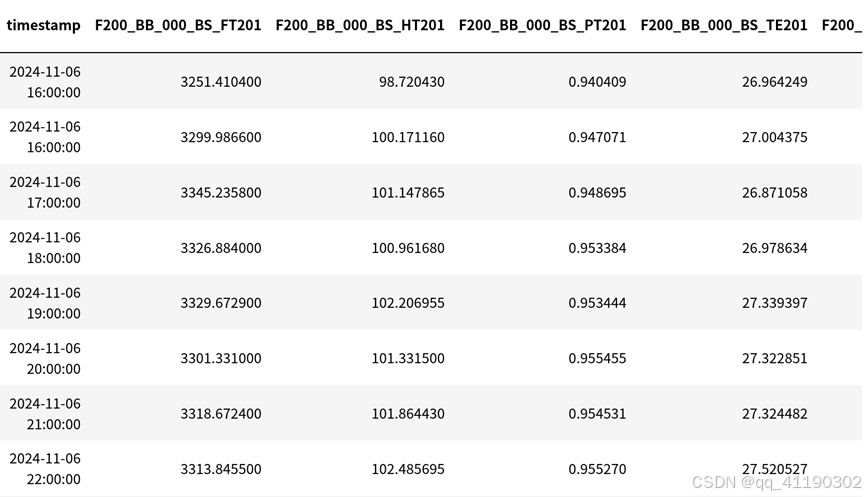
读入测点信息:
raw_taginfo = pd.read_csv('datasets/taginfo.csv', encoding="gbk") # 测点信息

从工况数据集中剥离出全部频率数据列,组成频率数据集,共1388行30列,将其视为可调整工况数据集。
taginfo = raw_taginfo[~raw_taginfo['disc'].str.contains('加压泵')] # 去掉加压泵全部工况信息
freq = raw_taginfo[raw_taginfo['disc'].str.contains('加压泵变频器运行频率')] # 保留加压泵频率信息
# taginfo = pd.concat([taginfo, freq], ignore_index=True)
tag = list(taginfo['tag']) # 工况测点名,需按照相关系数过滤
freq_tag = list(freq['tag']) # 频率测点名,不需过滤

读出的四个数据集——天气数据、工况数据集剩余部分、可调整工况数据集和测点信息数据中,根据时间戳合并天气与工况数据集剩余部分作为不可调整工况数据集,共1388行252列。
# 合并为数据集
data = raw_data.merge(raw_temp, on='timestamp', how='right')
data = data[~data['F200_BB_000_BS_FT201'].isna()]
data.reset_index(drop=True)
data.sort_values(by='timestamp', ascending=True)

3、相关性分析
确定需要优化的目标值——泵电流的累加值,对其进行归一化处理。
y_taginfo = raw_taginfo[raw_taginfo['disc'].str.contains('加压泵变频器运行电流')]
y_tag = list(y_taginfo['tag'])
y_data = data[y_tag]
# 各类工况下的加压泵总电流需求
y_data = y_data.sum(axis=1)
# 0-1归一化
y_data = (y_data - y_data.min()) / (y_data.max() - y_data.min())
# 计算奖励
rewards = -y_data
rewards = rewards.tolist()
计算不可调整工况数据集与目标值的spearman与皮尔逊相关系数`
# 计算相关系数
def getcorr(data, y):
# 0-1归一化
scaler = MinMaxScaler()
data = pd.DataFrame(scaler.fit_transform(data), columns=data.columns)
svalue_ls = [] # spearman相关系数
pvalue_ls = [] # 皮尔逊相关系数
for column, value in data.iteritems():
corr, pvalue = stats.spearmanr(value, y) # 返回两个浮点值
svalue_ls.append(corr)
pvalue_ls.append(pvalue)
# 去掉nan值
svalue_ls = np.nan_to_num(svalue_ls)
pvalue_ls = np.nan_to_num(pvalue_ls)
return svalue_ls, pvalue_ls, data
保留不可调整工况数据集中皮尔逊系数绝对值大于0.3或者spearman系数绝对值大于0.3的列,得到1388行123列。
# 工况数据
rawdata = data[tag]
taginfo['s_value'], taginfo['p_value'], rawdata = getcorr(rawdata, y_data)
# 选出皮尔逊系数绝对值大于0.3或者spearman系数绝对值大于0.3的参数
# 原始数据有重复列,应去掉
selected_tag = []
for index, row in taginfo.iterrows():
svalue = row['s_value']
pvalue = row['p_value']
if abs(svalue) >= 0.3 and row['tag'] not in selected_tag:
selected_tag.append(row['tag'])
elif abs(pvalue) >= 0.3 and row['tag'] not in selected_tag:
selected_tag.append(row['tag'])
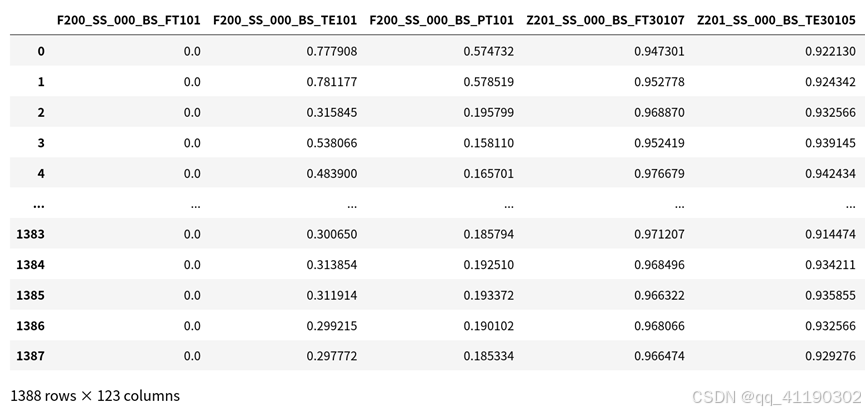
将水泵频率数据集(可调整工况数据集)在[0,50]归一化,计算与目标值的spearman相关系数。
# 频率数据
freq_rawdata = data[freq_tag]
# 频率上下限为【0,50】进行归一化处理
for column_name in freq_rawdata.columns:
freq_rawdata[column_name] = (freq_rawdata[column_name] - 0) / (50 - 0)
设置水泵相关性向量,若spearman系数绝对值大于0.1,则水泵相关性向量对应元素置1,否则置0,用于后期DDPG模型计算时过滤掉相关性过低的泵。30台泵相关性结果为:

4、原版DDPG模型与长输业务的整合
不可调整工况数据集对应DDPG模型的states,当前记录的下一个小时的记录对应next_state,水泵频率数据集(可调整工况数据集)对应actions,泵电流的累加值对应rewards。
训练分为两个阶段,一阶段:首先将一条不可调整工况数据信息(state)输入当前actor网络,得到30台水泵频率(action)的预测值。再将上一步的不可调整工况数据信息和水泵频率的预测值结合起来输入当前critic网络,得到当前工况下对应泵电流累加值的预测值r(s,a);二阶段:首先将当前记录的下一个小时的记录(next_state)输入目标actor网络,得到下一个小时不可调整工况下30台水泵频率的预测值(next_action),再将两个值结合起来输入目标critic网络,得到下一个小时工况下对应泵电流累加值的预测值r(s’,a’)。若当前工况下对应泵电流累加值的真实值为reward,设置折扣因子λ,则使用reward+λ·r(s’,a’)与r(s,a)的差值进行模型训练。

同时,由于原版模型只能得出reward的最优累加值,无法直接得出reward的最优值,设计一个新critic网络模型——pre_critic,将一条不可调整工况数据信息(state)和与之对应的30台水泵频率(action)的真实值输入该网络,得出reward的计算值。在分析预测阶段,将一条不可调整工况数据信息(state),及30台水泵频率(action)的预测值输入该模型,即可得出当前最优频率下电流的最优值。设计新网络后,原DDPG模型被修改为:

原版DDPG使用gym自带的环境:

本模型环境自行定义如下:
class Environment:
def __init__(self, states, actions, rewards):
self.set = []
self.states = states
for index, row in states.iterrows():
list = []
list.append(row.values) # 添加state
list.append(actions.iloc[index].values) # 添加action
list.append(rewards[index]) # 添加reward
if index < states.shape[0] - 1:
list.append(states.iloc[index + 1].values) # 添加next_state
list.append(0) # 添加done
else:
list.append(None) # 添加next_state
list.append(1) # 添加done
self.set.append(list)
# 初始状态
def reset(self):
return self.set[0][0]
def reset2(self):
pos = random.randint(0, self.states.shape[0] - 2)
return pos, self.set[pos][0]
def reset3(self):
pos = random.randint(0, self.states.shape[0] - 2)
return pos, self.set[pos][0], self.set[pos][1]
# 获取当前行为的下一个状态、奖励
def step(self, index):
return self.set[index][3], self.set[index][2]
# 获取当前行为的下一个done,用于判定下一条是否是最后一条
def next_done(self, index):
return self.set[index][4]
原模型网络参数为:
agent = DDPG(alpha=0.0003, beta=0.0003, state_dim=env.observation_space.shape[0],
action_dim=env.action_space.shape[0], actor_fc1_dim=400, actor_fc2_dim=300,
critic_fc1_dim=400, critic_fc2_dim=300, ckpt_dir=args.checkpoint_dir,
batch_size=256)
根据长输业务特点,调整为:
agent = DDPG(alpha=0.001, beta=0.001, state_dim=n_states,
action_dim=n_actions, actor_fc1_dim=n_hiddens, actor_fc2_dim=n_hiddens,
critic_fc1_dim=n_hiddens, critic_fc2_dim=n_hiddens, ckpt_dir=args.checkpoint_dir,
gamma=0.99, tau=0.001, max_size=int(data_size * 0.1), batch_size=1,
corr=actions_s_value)
其中,隐层节点数n_hiddens使用state与action数量的乘积再开方确定。
n_hiddens = round(math.sqrt(n_states*n_actions)) # 隐层节点数
将业务约束,及水泵相关性列向量加入当前actor网络与目标actor网络的训练与预测中。
def forward(self, state):
x = T.relu(self.ln1(self.fc1(state)))
x = T.relu(self.ln2(self.fc2(x)))
action = T.tanh(self.action(x))
# 结合业务实际进行修改
action = (action + 1) / 2 # 为了更贴合业务实际,缩放到 [0, 1]
action = action.detach().cpu().numpy()
freq_ls = []
for i in range(len(action)): # 业务约束,推荐开启的泵频率不小于30,归一化后为0.6,小于进行处理,有的设为30,有的则抛弃,认为此泵不该开启
if action[i] < 0.6:
action[i] = 0
freq_ls.append(action[i])
# 相同泵组只要泵开启,则频率应大致相同
# 30台泵,每5个一组,共6组
c = 1
sum = 0
pos_ls = []
for j in range(len(freq_ls)):
if freq_ls[j] > 0:
sum += freq_ls[j]
pos_ls.append(j)
if c == 5:
if len(pos_ls) > 0:
avg = sum / len(pos_ls)
for pos in pos_ls:
action[pos] = avg
c = 1
sum = 0
pos_ls = []
else:
c += 1
action *= self.corr # 丢掉相关性过低的泵
action = T.from_numpy(action).to(device)
return action
同时,重写噪声机制,用频率预测值与真实值误差替换,误差大则扰动大,反之亦然。
# 根据业务特点重写噪声机制,增加搜索
# noise考虑用误差替换,误差大则扰动大,反之亦然
real_action = T.tensor(real_action, dtype=T.float).to(device)
self.action_noise = F.mse_loss(action, real_action).detach().cpu().numpy()
noise = T.tensor(np.random.normal(loc=0.0, scale=self.action_noise, size=action.size(0)),
dtype=T.float).to(device)
# 根据业务特点,action值范围在【0,1】之间
action = T.clamp(action + noise, 0, 1)
四个原版DDPG模型定义如下:
self.actor = ActorNetwork(alpha=alpha, state_dim=state_dim, action_dim=action_dim,
fc1_dim=actor_fc1_dim, fc2_dim=actor_fc2_dim, corr=corr)
self.target_actor = ActorNetwork(alpha=alpha, state_dim=state_dim, action_dim=action_dim,
fc1_dim=actor_fc1_dim, fc2_dim=actor_fc2_dim, corr=corr)
self.critic = CriticNetwork(beta=beta, state_dim=state_dim, action_dim=action_dim,
fc1_dim=critic_fc1_dim, fc2_dim=critic_fc2_dim)
self.target_critic = CriticNetwork(beta=beta, state_dim=state_dim, action_dim=action_dim,
fc1_dim=critic_fc1_dim, fc2_dim=critic_fc2_dim)
自定义的pre_critic网络如下:
# 增添一个网络,用于预测reward
self.pre_critic = CriticNetwork(beta=beta, state_dim=state_dim, action_dim=action_dim,
fc1_dim=critic_fc1_dim, fc2_dim=critic_fc2_dim)
5、DDPG模型训练
对整个数据集训练10轮共1388*10步,每10步记录一次结果:
avg_reward_history.append(avg_reward)
print('Ep: {} Reward: {:.6f} AvgReward: {:.6f}'.format(episode + 1, total_reward, avg_reward))
if (episode + 1) % 10 == 0:
agent.save_models(episode + 1)
# -------------------------------------- #
# 绘图
# -------------------------------------- #
episodes = [i + 1 for i in range(len(avg_reward_history))]
plot_learning_curve(episodes, avg_reward_history, title='episode',
ylabel='mean_return', figure_file=args.figure_file)
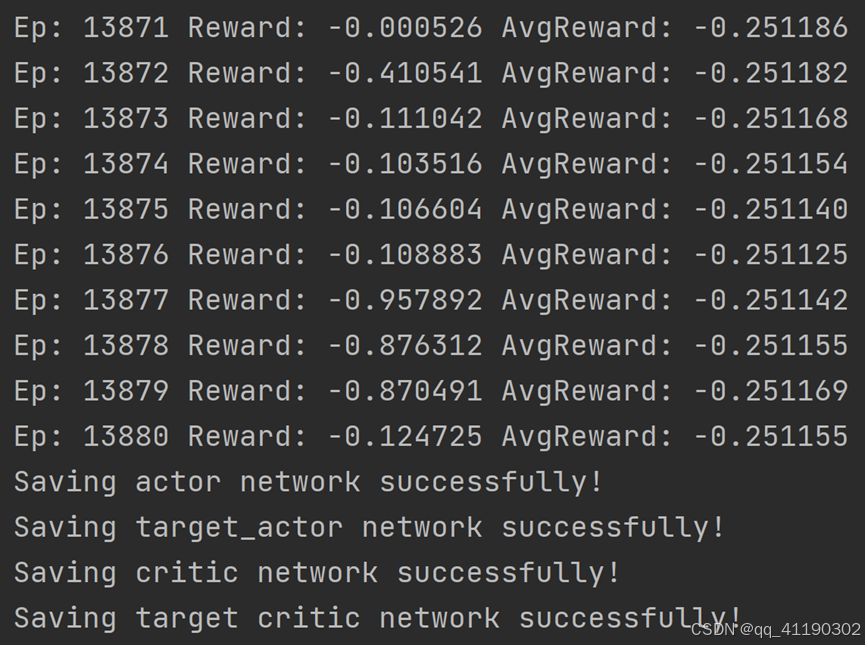
可视化结果:

模型在8000步之后基本趋于稳定。
6、DDPG模型预测
利用模型进行分析预测。
# 计算 输出结果为当前时刻的预测动作、动作在一段样本内的平均回报
def calculate(self, episode, state, max_step):
self.load_models(episode)
# 根据state预测action
self.actor.eval()
state = T.tensor(state, dtype=T.float).to(device)
action = self.actor.forward(state).squeeze()
# 结合当前状态和计算出的行为,计算对应奖励值
reward = self.pre_critic.forward(state, action).view(-1)
return action.detach().cpu().numpy(), -reward.detach().cpu().numpy()[0] / max_step
以2025-01-01 03:00:00时刻数据为例,模型分析结果如下:
# 还原电流
reward = anti_norm_elec(elec_value, reward)
elec_value['timestamp'] = timestamps
elec_value = elec_value[elec_value['timestamp'] <= current_timestamp].sort_values(by='timestamp',
ascending=False).head(1)
real_elect = elec_value.drop('timestamp', axis=1).iloc[0].sum()
print('当前实际总电流(A):' + str(real_elect))
print('当前总电流优化值(A):' + '{:.2f}'.format(reward))

经优化调整后,总电流由1155.15A降至1094.16A,降低5.27%,符合业务要求。
完整方案+数据集下载地址:
https://pan.baidu.com/s/1lWGPajPp18DZflWTKKhKAw
提取码: m7av

























 5万+
5万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










