机器学习（四）——用解析解的方式求解模型

最新推荐文章于 2022-12-18 00:33:22 发布

qq_41386300

最新推荐文章于 2022-12-18 00:33:22 发布

阅读量1k

点赞数 1

分类专栏：机器学习

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/qq_41386300/article/details/98472373

版权

本文介绍了机器学习中的最大似然估计原理，通过中心极限定理来理解数据分布，并详细阐述了概率密度函数、损失函数的概念。接着，文章通过解析解的方式解释了线性回归的优化过程，最终给出了使用代码实现解析解的示例，包括直接实现和使用sklearn库的简化方式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

最大似然估计

在这里插入图片描述
通俗来讲：假设你有一组身高的数据，有两个正态分布（踢足球的和打篮球的），打篮球的正态分布肯定是那种又细又高的，而踢足球的是宽低的，
最大似然估计就是，把数据带进去看它属于哪个正态分布，假设有个一米九的，我们就可以猜出他是打篮球的

中心极限定理

在这里插入图片描述
在这里，我们的随机变量是误差的值

概率密度函数

在这里插入图片描述
概率密度函数：当f（x）越大说明某个x出现在这个正态分布上的概率越大
f（x）并不是概率，而是概率密度，因为概率不好求，所以我们求概率密度，如下图

上图中的阴影部分的面积就是概率，它不好求，需要积分，所以我们用概率密度代替，效果一样，当概率密度最大的时候就是最优解

损失函数

下图是化解步骤：
在这里插入图片描述
L：最大总似然估计：m个样本里的每个样本的似然相乘

因为相乘不好算，所以我们取对数

取对数可以把连乘变成连加，如下
在这里插入图片描述
上图中第四行：减号前面的值是固定的，所以减号后面的值越小整个值就越大
所以上图中最后的式子就是我们的线性回归的损失函数，我们要求得就是损失函数最小的时候

解析解

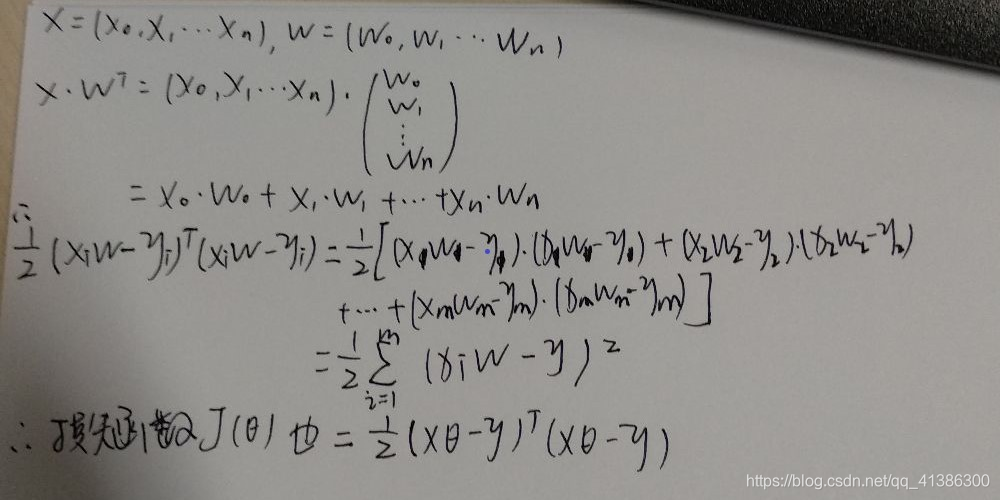
在这里插入图片描述

在这里插入图片描述

代码实现

用代码实现——用解析解的方式求解模型

import numpy as np
import matplotlib.pyplot as pl

最低0.47元/天解锁文章

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。