神经网络中的单层神经网络

文章综合一下几位大佬的文章：

杨强AT南京: DL01-6: 单层神经网络
企鹅号 - 轨道车辆: 技术篇：单层神经网络是什么，看完这篇文章你就懂了

一、神经网络

1.概述

神经网络是一种模拟人脑的神经网络以期能够实现类人工智能的机器学习技术。人脑中的神经网络是一个非常复杂的组织。成人的大脑中估计有1000亿个神经元之多。

看一个经典的神经网络。这是一个包含三个层次的神经网络。
🔹 红色的是输入层，绿色的是输出层，紫色的是中间层（也叫隐藏层）。
🔹 输入层有3个输入单元，隐藏层有4个单元，输出层有2个单元。

1.1 结构

神经元模型是一个包含输入，输出与计算功能的模型。输入可以类比为神经元的树突，而输出可以类比为神经元的轴突，计算则可以类比为细胞核。

📢 设计一个神经网络时，输入层与输出层的节点数往往是固定的，中间层则可以自由指定；

📢 神经网络结构图中的拓扑与箭头代表着预测过程时数据的流向，跟训练时的数据流有一定的区别；

📢 结构图里的关键不是圆圈（代表“神经元”），而是连接线（代表“神经元”之间的连接）。每个连接线对应一个不同的权重（其值称为权值），这是需要训练得到的。

下图是一个典型的神经元模型：包含有3个输入，1个输出，以及2个计算功能。

注意中间的箭头线。这些线称为“连接”。每个上有一个“权值”。

📢 连接是神经元中最重要的东西。每一个连接上都有一个权重。

一个神经网络的训练算法就是让权重的值调整到最佳，以使得整个网络的预测效果最好。

我们使用a来表示输入，用w来表示权值。一个表示连接的有向箭头可以这样理解：在初端，传递的信号大小仍然是a，端中间有加权参数w，经过这个加权后的信号会变成aw，因此在连接的末端，信号的大小就变成了aw。

在其他绘图模型里，有向箭头可能表示的是值的不变传递。而在神经元模型里，每个有向箭头表示的是值的加权传递。如果我们将神经元图中的所有变量用符号表示，并且写出输出的计算公式的话，就是下图。

1.2 神经元模型使用

我们有一个数据，称之为样本。样本有四个属性，其中三个属性已知，一个属性未知。我们需要做的就是通过三个已知属性预测未知属性。

具体办法就是使用神经元的公式进行计算。三个已知属性的值是a1，a2，a3，未知属性的值是z。z可以通过公式计算出来。

这里，已知的属性称之为特征，未知的属性称之为目标。假设特征与目标之间确实是线性关系，并且我们已经得到表示这个关系的权值w1，w2，w3。那么，我们就可以通过神经元模型预测新样本的目标。

2. 单层神经网络

2.1 感知器

来自百度百科：感知器 （神经网络模型）

1958年，计算科学家Rosenblatt提出了由两层神经元组成的神经网络。他给它起了一个名字–“感知器”（Perceptron），也可翻译为感知机。

神经细胞

---

感知器是生物神经细胞的简单抽象，神经细胞结构大致可分为：树突、突触、细胞体及轴突。

单个神经细胞可被视为一种只有两种状态的机器——激动时为‘是’，而未激动时为‘否’。神经细胞的状态取决于从其它的神经细胞收到的输入信号量，及突触的强度（抑制或加强）。当信号量总和超过了某个阈值时，细胞体就会激动，产生电脉冲。电脉冲沿着轴突并通过突触传递到其它神经元。

为了模拟神经细胞行为，与之对应的感知机基础概念被提出，如权量（突触）、偏置（阈值）及激活函数（细胞体）。

在人工神经网络领域中，感知器作为一种线性分类器，也被指为单层的人工神经网络，以区别于较复杂的多层感知器（Multilayer Perceptron）。

📢 在“感知器”中，有两个层次:

• 输入层
  输入层里的“输入单元”只负责传输数据，不做计算。
• 输出层
  输出层里的“输出单元”则需要对前面一层的输入进行计算。

把需要计算的层次称之为“计算层”，并把拥有一个计算层的网络称之为“单层神经网络”。有一些文献会按照网络拥有的层数来命名，例如把“感知器”称为两层神经网络。

假如我们要预测的目标不再是一个值，而是一个向量，例如[x,y]。那么可以在输出层再增加一个“输出单元”,如图：

2.2 数学描述

感知器使用特征向量来表示的前馈式人工神经网络，它是一种二元分类器，把矩阵上的输入（实数值向量）映射到输出值 $f(x)$上（一个二元值）。
$$f(x)=\{\begin{array}{l}1,ifw\ast x+b>0\\ 0,else\end{array}$$
$w$是实数的表权重的向量，$w\ast x$是点积。$b$是偏置，一个不依赖于任何输入值的常数。偏置可以认为是激励函数的偏移量，或者给神经元一个基础活跃等级。

$f(x)$ (0 或 1)用于分类，判断是肯定的还是否定的，这属于二元分类问题。如果$b$是负的，那么加权后的输入必须产生一个肯定的值并且大于 $b$，这样才能令分类神经元大于阈值0。从空间上看，偏置改变了决策边界的位置（虽然不是定向的）。

由于输入直接经过权重关系转换为输出，所以感知机可以被视为最简单形式的前馈式人工神经网络。

2.3 感知器分类效果

与神经元模型不同，感知器中的权值是通过训练得到的。因此，根据以前的知识我们知道，感知器类似一个逻辑回归模型，可以做线性分类任务。

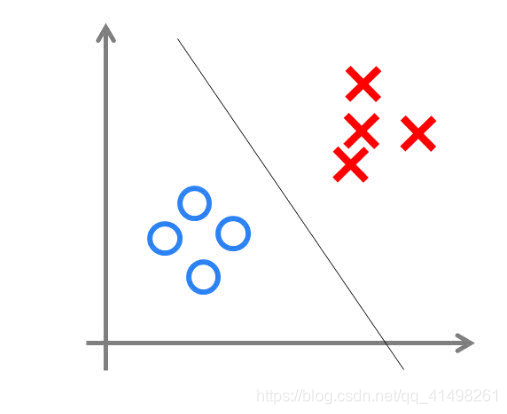
我们可以用决策分界来形象的表达分类的效果。决策分界就是在二维的数据平面中划出一条直线，当数据的维度是3维的时候，就是划出一个平面，当数据的维度是n维时，就是划出一个n-1维的超平面。

2.4 单层神经网络表示

单层多感知器神经网络图示如下：
 其中数据表示如下：

1. 输入数据向量: $\overrightarrow{X}=\left[\begin{array}{cccc}{x}_0& x_1& \dots & x_n\end{array}\right]$ (矩阵表示为：X)
2. 输出数据向量：$\overrightarrow{Y}=\left[\begin{array}{cccc}{y}_0& y_1& \dots & y_m\end{array}\right]$ (矩阵表示为：Y)
3. 权重矩阵：$W=\left[\begin{array}{cccc}{\omega }_{00}& {\omega }_{01}& \dots & {\omega }_{0n}\\ {\omega }_{10}& {\omega }_{11}& \dots & {\omega }_{1n}\\ \dots & \dots & \dots & \dots \\ {\omega }_{m0}& {\omega }_{m1}& \dots & {\omega }_{mn}\end{array}\right]$
   （n是输入特征数据长度，m数输出特征数据长度）
   （权重的每一行对应着一个感知器的权重，m行就意味着m个感知器）

2.5 单层神经网络训练算法

单层神经网络训练依据是基于如下目标：
  就是找到一组感知器的权重，使得这组感知器的输出$Y$与期望输出$\bar{Y}$之间的误差最小。

第一步：初始化一个随机权重矩阵（用来训练）；
第二步：输入特征数据$X$计算每个感知器($m$个感知器)的输出$y_i(i=1,2,\dots ,m)$，每个感知器的权重对应权重矩阵$W$中的一行，多个感知的输出就是输出向量$Y$
第三步：计算感知器输出向量$Y$与样本期望输出$\bar{Y}$之间的误差。
第四步：根据计算的误差，计算权重矩阵的更新梯度。
第五步：用更新梯度，更新权重矩阵。
第六步：然后从第二步反复执行，直到训练结束（训练次数根据经验自由确定）

2.6 单层神经网络中的计算公式表示

在上面描述的训练过程中，有两个主要的计算公式：

1. 感知器输出计算。
2. 权重的更新计算（核心是计算更新梯度）。

其中权重梯度的计算有两个依据：

1. 误差的度量标准：损失函数的定义；
2. 误差最小：损失函数极小值计算。

根据这两个依据，我们可以列出单层神经网络的计算公式如下：

单层多感知器的计算输出公式：

$$Y^T=W\bullet X^T+W_b$$
$X：输入特征数据，使用行向量表示.$
$W_b：表示加权求和的偏置项$。

如果考虑激活函数，则计算输出公式为：

$$Y^T=f_{activity}(W\bullet X^T+W_b)$$

单层多感知器的权重计算公式：

$$W_{new}=W_{old}-\eta \ast {\nabla }_W$$
$$w_i^{new}=w_i^{old}-\eta \ast {\nabla }_{w_i}$$
$i$：表示第i个感知器
$\eta$：表示学习率，用来控制训练速度。
${\nabla }_{w_i}$：表示更新梯度（因为误差最小，是梯度下降，所以梯度更新是减去(-)梯度），梯度使用损失函数的导数，表示如下：
$${\nabla }_{w_i}=\frac{\partial E(w_i)}{\partial w_i}$$