LeetCode刷题小技巧-错题记录本-C++版本

#include<bits/stdc++.h>

using namespace std;
typedef pair<string, int> Pair;

//第3参数为函数名
bool my_compare(const Pair &p1, const Pair &p2){
	return p1.second < p2.second;
}

//第3参数为重载了operator()操作符的类对象
struct MyCompare{
public:
	bool operator()(const Pair &p1, const Pair &p2) const{
		return p1.second < p2.second;
	}
};
int main(){
	map<string, int> test;
	test["Alice"] = 3;
	test["Cindy"] = 5;
	test["Bob"] = 7;

	cout << "> sort by key" << endl;
	for(auto itr = test.begin(); itr != test.end(); ++itr){
		cout << itr->first << ": " << itr->second << endl;
	}
	cout << endl;

	vector<Pair> vec;

	for(auto itr = test.begin(); itr != test.end(); ++itr){
		vec.push_back(make_pair(itr->first, itr->second));
	}

	sort(vec.begin(), vec.end(), MyCompare()); //my_compare或者MyCompare()都可以

	cout << "> sort by value" << endl;
	for(auto itr = vec.begin(); itr != vec.end(); ++itr){
		cout << itr->first << ": " << itr->second << endl;
	}

	return 0;
}

二是通过将map的key和value位置替换

#include<bits/stdc++.h>

using namespace std;
typedef pair<string, int> Pair;

int main(){
	map<string, int> test;
	test["Alice"] = 3;
	test["Cindy"] = 5;
	test["Bob"] = 7;

	cout << "> sort by key" << endl;
	for(auto itr = test.begin(); itr != test.end(); ++itr){
		cout << itr->first << ": " << itr->second << endl;
	}
	cout << endl;

	map<int, string> result;
	transform(test.begin(), test.end(), inserter(result, result.begin()), [](pair<string, int> a) { return pair<int, string>(a.second, a.first); });

	cout << "> sort by value" << endl;
	for(auto itr = result.begin(); itr != result.end(); ++itr){
		cout << itr->first << ": " << itr->second << endl;
	}

	return 0;
}

3，pair的认识

1，pair是将2个数据组合成一个数据，当需要这样的需求时就可以使用pair，如stl中的map就是将key和value放在一起来保存。另一个应用是，当一个函数需要返回2个数据的时候，可以选择pair。 pair的实现是一个结构体，主要的两个成员变量是first second 因为是使用struct不是class，所以可以直接使用pair的成员变量。

2，
template pair make_pair(T1 a, T2 b) { return pair(a, b); }
很明显，我们可以使用pair的构造函数也可以使用make_pair来生成我们需要的pair。一般make_pair都使用在需要pair做参数的位置，可以直接调用make_pair生成pair对象很方便，代码也很清晰。另一个使用的方面就是pair可以接受隐式的类型转换，这样可以获得更高的灵活度。

3，对于pair类，由于它只有两个元素，分别名为first和second，因此直接使用普通的点操作符即可访问其成员。

4，质数判断的方法

1，常见方法，直接通过遍历到n的开平法进行整除判断，效率不高。

2，通过标志方法，设置一个bool数组，先进行初始化，奇数设置为true，偶数设置为false，只需将前面为true表示为质数的倍数设置为flase即可，效率较上面高。

3，质数分布的规律：大于等于5的质数一定和6的倍数相邻。例如5和7，11和13,17和19等等；
bool isPrime( int num )
{
    //两个较小数另外处理
    if(num == 2||num == 3 )
        return 1;
    //不在6的倍数两侧的一定不是质数
    if(num % 6 != 1&&num % 6 != 5)
        return 0;
    int tmp = sqrt(num);
    //在6的倍数两侧的也可能不是质数
    for(int i = 5;i <= tmp;i += 6)
        if(num %i == 0||num % (i+ 2) == 0)
            return 0;
    //排除所有，剩余的是质数
    return 1;

}

5，自定义数据结构的根堆（Priority_queue）

1，方法一

必须自己重载 operator< 或者自己写仿函数（有些编译器重载运算符会很坑，还是两个都掌握的比较稳妥）。
重载运算符，推荐采用下面这种方法：
struct cow {
    int s, e;
    cow(int a = 0, int b = 0) { s = a, e = b; }
}c[MAX];

bool operator<(const cow & c1, const cow & c2) {
    return c1.s < c2.s;
}
priority_queue<cow>q;

2，方法二

自己写仿函数，也就是刚才出现的greater<int>这种函数，怎么写呢？
struct cow {
    int s, e;
    cow(int a = 0, int b = 0) { s = a, e = b; }
}c[MAX];
struct cmp {
    bool operator()(cow c1, cow c2) {
        return c1.s < c2.s;
    }
};
priority_queue<cow, vector<cow>, cmp>p;

6，用栈实现二叉树的中序遍历和后序遍历

1，中序遍历

class Solution {
public:
    vector<int> inorderTraversal(TreeNode *root) {
        vector<int> res;
        stack<TreeNode*> s;
        TreeNode *p = root;
        while (p || !s.empty()) {
            while (p) {
                s.push(p);
                p = p->left;
            }
            p = s.top(); s.pop();
            res.push_back(p->val);
            p = p->right;
        }
        return res;
    }
};

2，后序遍历

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        stack<TreeNode*> s1;
        stack<TreeNode*> s2;
        vector<int> res;
        if(!root){
            return res;
        }
        s1.push(root);
        while(!s1.empty()){
            TreeNode* cur = s1.top();
            s1.pop();
            s2.push(cur);
            //先将left压到栈里，再将right压到栈里，然后取出将右子树压到s2
            //中，最后再压左子树
            //待右子树全部压完，然后将左子树全部压到栈s2中
            //此时栈s2从上到下依次是左子树、右子树、根
            if(cur->left){
                s1.push(cur->left);
            }
            //后压右子树，然后全部将有子树压到栈s2中
            if(cur->right){
                s1.push(cur->right);
            }
        }
        while(!s2.empty()){
            //弹出s2栈顶元素，依次尾插到vector中，最终得到二叉树的后序
            //遍历
            res.push_back(s2.top()->val);
            s2.pop();
        }
        return res;
    }
};

7，怎样判断一个整数是否能由另一个整数平方得到

int t1;// 目标整数

int t2=sqrt(t1);

if(t2*t2==t1)return "t1能够开平方且开平方后的数为整数";

8，用vector定义固定长度的二维数组

vector>dp(col,vector(row,0));//定义行col列row的二维数组dp[col][row];

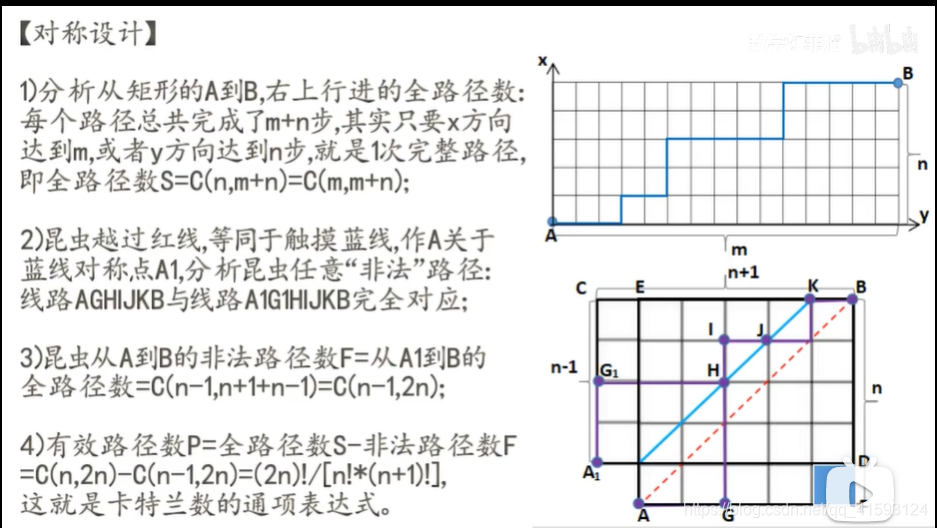
9，明安图数-卡特兰数的计算以及常见的应用

百度百科的定义：

明安图数，又称卡塔兰数，英文名Catalan number，是组合数学中一个常出现于各种计数问题中的数列。以中国蒙古族数学家明安图 (1692-1763)和比利时的数学家欧仁·查理·卡塔兰 (1814–1894)的名字来命名，其前几项为（从第零项开始） : 1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, 129644790, 477638700, 1767263190, 6564120420, 24466267020, 91482563640, 343059613650, 1289904147324, 4861946401452, ...
int catalan(int n){

    if (n == 0)return 1;
    if (n == 1)return 1;
    int res = 0;
    for (int i = 0; i <=n-1;i++){
        res += catalan(i)*catalan(n-1-i);
    }
    return res;

}
明安图数的应用：

（1）括号化

矩阵连乘： P=a1×a2×a3×……×an，依据乘法结合律，不改变其顺序，只用括号表示成对的乘积，试问有几种括号化的方案。（ h(n) 种）

（2）出栈次序

一个栈(无穷大)的进栈序列为1，2，3，…，n，有多少个不同的出栈序列? [5-6]

（3）凸多边形三角划分

在一个凸多边形中，通过若干条互不相交的对角线，把这个多边形划分成了若干个三角形。任务是键盘上输入凸多边形的边数n，求不同划分的方案数f（n）。比如当n=6时，f（6）=14。

（4）给定节点组成二叉搜索树

给定N个节点，能构成多少种不同的二叉搜索树。

（能构成 h(N) 个）

（这个公式的下标是从h(0)=1开始的）

（5）n对括号正确匹配数目

给定n对括号，求括号正确配对的字符串数，例如：

0对括号：[空序列] 1种可能

1对括号：() 1种可能

2对括号：()() (()) 2种可能

3对括号：((())) ()(()) ()()() (())() (()()) 5种可能

百度百科：https://baike.baidu.com/item/%E5%8D%A1%E7%89%B9%E5%85%B0%E6%95%B0/6125746?fr=aladdin#reference-[5]-2499752-wrap

10，用深度遍历实现元素互不相同数组全排列思想

深度遍历+备忘录visited[]可以解决很多实际问题，例如迷宫、数组下标选择问题等。

11，树状数组思想

树状数组或二叉索引树（英语：Binary Indexed Tree），又以其发明者命名为Fenwick树，最早由Peter M. Fenwick于1994年以A New Data Structure for Cumulative Frequency Tables为题发表在SOFTWARE PRACTICE AND EXPERIENCE。其初衷是解决数据压缩里的累积频率（Cumulative Frequency）的计算问题，现多用于高效计算数列的前缀和，区间和。
class BIT {
private:
    vector<int> tree;
    int n;

public:
    BIT(int _n): n(_n), tree(_n + 1) {}

    static constexpr int lowbit(int x) {
        return x & (-x);
    }

    void update(int x, int d) {
        while (x <= n) {
            tree[x] += d;
            x += lowbit(x);
        }
    }

    int query(int x) const {
        int ans = 0;
        while (x) {
            ans += tree[x];
            x -= lowbit(x);
        }
        return ans;
    }
};