球相交的表面积并/体积并

最新推荐文章于 2022-04-14 10:35:18 发布

JZK-Keven

最新推荐文章于 2022-04-14 10:35:18 发布

阅读量2.3k

点赞数 2

分类专栏：牛客网

本文链接：https://blog.csdn.net/qq_41608020/article/details/103842879

版权

牛客网专栏收录该内容

30 篇文章

订阅专栏

什么是球冠和球缺

如上图，是一个以 $O$ 点为球心， $R$ 为半径，截去下半部分的球冠，它的表面积和体积公式如下：

$S=2*\Pi*R*H$

$V=\Pi*R^2*\frac{3*R-H}{3}$

如果我们可以得到 $H$ 和 $R$ 的值，那么我们就可以知道这个球缺的表面积和体积，所以对于球相交的表面积和体积这类问题，只要求出 $H$ ，基本上就做完啦。

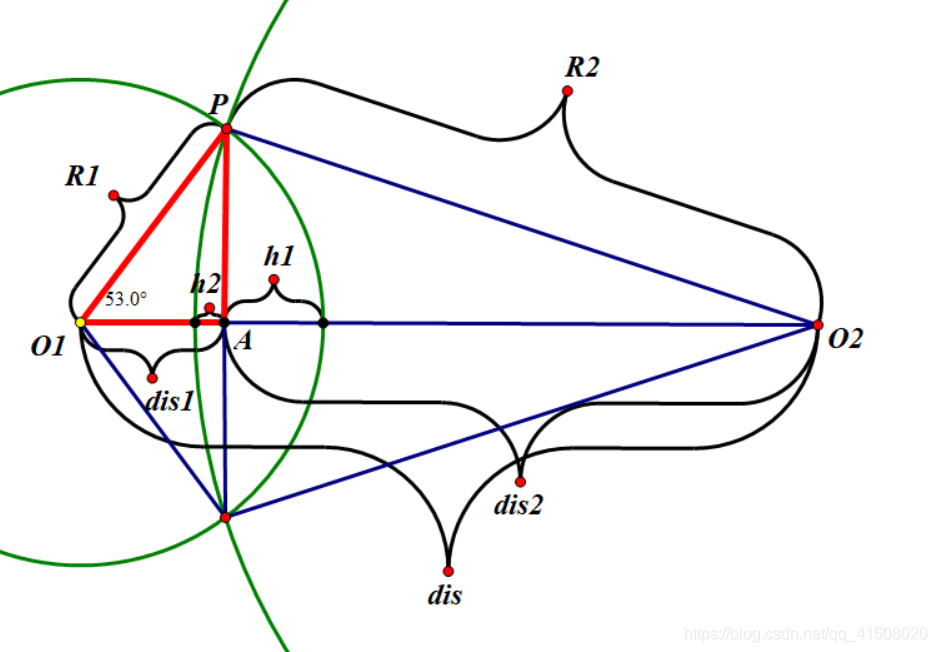
我们已知两个球的球心和半径，需要求两个球的表面积并/体积。

显然两个球相交的相交部分是两个球缺，所以我们只需要求出这两个球的球缺的表面积/体积，就可以算出答案，要求出球缺的表面积/体积，并且已知球的半径 $R$ ，显然只需要求出球缺的高 $H$ 就可以了。

下面我以求球 $O1$ 的高 $H$ 为例，先求出圆心之间的距离 $dis$ ，已知 $R1,R2,dis$ ，由 $\Delta \ P\ O1\ O2$ 和余弦定理，可以求出 $\angle \ P\ O1 \ O2$ 的值，然后由直角三角形 $\Delta \ P\ O1\ A$ 可以求出线段 $A\ O1$ 的长度 $dis$ ，最后 $h1=R1-dis1$ 。

然后用两个球的总表面积/体积减去两个球缺的总表面积/体积就可以得到答案了。

注意，一般这样的题目要先判断两个球的关系是内含、相交，还是外离。若内含或外离，直接输出答案即可。

牛客小白月赛20 C

球的表面积并

Code：

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const double PI = acos(-1.0);
struct point
{
    double x;
    double y;
    double z;
};
struct circle
{
    point o;
    double r;
} a, b;
double getlen(point a, point b)
{
    double ans = sqrt((a.x - b.x) * (a.x - b.x) + (a.y - b.y) * (a.y - b.y) + (a.z - b.z) * (a.z - b.z));
    return ans;
}
int main()
{
    scanf("%lf%lf%lf%lf", &a.o.x, &a.o.y, &a.o.z, &a.r);
    scanf("%lf%lf%lf%lf", &b.o.x, &b.o.y, &b.o.z, &b.r);
    assert(-100000 <= a.o.x && a.o.x <= 100000);
    assert(-100000 <= a.o.y && a.o.y <= 100000);
    assert(-100000 <= a.o.z && a.o.z <= 100000);
    assert(0 < a.r && a.r <= 100000);
    assert(-100000 <= b.o.x && b.o.x <= 100000);
    assert(-100000 <= b.o.y && b.o.y <= 100000);
    assert(-100000 <= b.o.z && b.o.z <= 100000);
    assert(0 < b.r && b.r <= 100000);
    if (a.r > b.r)
        swap(a, b);
    double dis = getlen(a.o, b.o);
    if (dis + a.r <= b.r)
    {
        double r = max(a.r, b.r);
        double ans = 4 * PI * r * r;
        printf("%.6lf", ans);
    }
    else if (dis < a.r + b.r && dis + a.r > b.r)
    {
        double angle_cosa = (a.r * a.r + dis * dis - b.r * b.r) / (2 * a.r * dis);
        double angle_cosb = (b.r * b.r + dis * dis - a.r * a.r) / (2 * b.r * dis);
        double len_a = a.r - a.r * angle_cosa;
        double len_b = b.r - b.r * angle_cosb;
        double ans = 4 * PI * (a.r * a.r + b.r * b.r);
        ans -= 2 * PI * (a.r * len_a + b.r * len_b);
        printf("%.6lf", ans);
    }
    else
    {
        double ans = 4 * PI * (a.r * a.r + b.r * b.r);
        printf("%.6lf", ans);
    }
}

Wannafly winter camp 2019 day2 H

球的体积并

code:

#include <bits/stdc++.h>
const double PI = acos(-1.0);
using namespace std;
struct node
{
	double x;
	double y;
	double z;
	double r;
}que[105], o;
double calc(node o, node t)
{
	if (o.r < t.r)
		swap(o, t);
	double dis = sqrt((o.x - t.x)*(o.x - t.x) + (o.y - t.y)*(o.y - t.y) + (o.z - t.z)*(o.z - t.z));
	if (dis <= o.r - t.r)
	{
		return 4.0 / 3 * PI * t.r * t.r * t.r;
	}
	else if (dis <= o.r)
	{
		double angleb = acos((t.r*t.r + dis * dis - o.r*o.r) / (2 * t.r * dis));
		double anglea = PI - angleb;
		double l = t.r*cos(anglea);
		double H = o.r - l - dis;
		double h = t.r - l;
		return 4.0 / 3 * PI * t.r * t.r * t.r - PI / 3 * (3 * t.r - h)*h*h + PI / 3 * (3 * o.r - H)*H*H;
	}
	else if (dis < o.r + t.r)
	{
		double angler = acos((t.r*t.r + dis * dis - o.r*o.r) / (2 * t.r * dis));
		double angleR = acos((o.r*o.r + dis * dis - t.r*t.r) / (2 * o.r * dis));
		double H = o.r - o.r * cos(angleR);
		double h = t.r - t.r * cos(angler);
		return PI / 3 * (3 * t.r - h)*h*h + PI / 3 * (3 * o.r - H)*H*H;
	}
	return 0;
}
int main()
{
	int t, n, cas = 1;
	scanf("%d", &t);
	while (t--)
	{
		scanf("%d", &n);
		for (int i = 0; i < n; i++)
			scanf("%lf%lf%lf%lf", &que[i].x, &que[i].y, &que[i].z, &que[i].r);
		scanf("%lf%lf%lf%lf", &o.x, &o.y, &o.z, &o.r);
		double ans = 0;
		for (int i = 0; i < n; i++)
			ans += calc(o, que[i]);
		printf("Case #%d: %.6lf\n", cas++, ans);
	}
}