参考资料:
F. Moukalled, L. Mangani, M. Darwish. The finite volume method in computational fluid dynamics. An advanced introduction with Openfoam and Matlab[M]. Chapter13:Temporal discretization: the transient term
简介:本章介绍了一种瞬态项有限积分离散方法(书上介绍了两种,本文省略了有限差分法),基本思想是在一个拟时间单元上采用与对流项离散类似的方法对瞬态项离散。
1. 瞬态项离散
瞬态问题的控制方程为
经空间积分和离散后,上式可写为
其中是在一个参考时刻t时的非瞬态项空间离散结果,可表达为
当t趋向于无穷大时,瞬态离散方程趋近于定常方程,这一情况与利用时间推进法求解定常问题一致。现介绍瞬态项离散方法。
瞬态项的有限体积离散方法与对流项的离散方法十分相近,除了积分是对时间积分而不是对空间积分。对从
进行积分,可得
将VC视为常数,上式结果为
等价于
现需要根据和t处(单元上)参数值确定
和
处(界面上)参数值(也就是确定插值型线),最后离散方程为
上标k-1表示上一时间步计算结果,最后更新代数方程组系数:
1)一阶瞬态格式
一阶隐式和显式欧拉格式分别基于一阶迎风格式和背风格式。
a. 一阶隐式欧拉格式
首先介绍基于一阶迎风格式的隐式欧拉格式。在隐式欧拉格式下,界面上参数值取上一时间步的参数值:
因此取为

由于该格式为一阶格式,会产生数值耗散(上标圆圈与k-1意义一致),由泰勒展开式得

整理为

代入离散方程中,有

该格式即使在时间步长很大的情况下,依旧是稳定的。
b. 一阶显式欧拉格式
一阶显式欧拉格式采用的是背风插值型线,即界面,
上参数值取下一时间步参数值:
因此取为

该格式为显式格式,其包含假设:的对流在整个时间步始终占主导。该格式会产生数值反耗散,t+dt对t做泰勒展开,为

整理为

代入离散方程 中,有
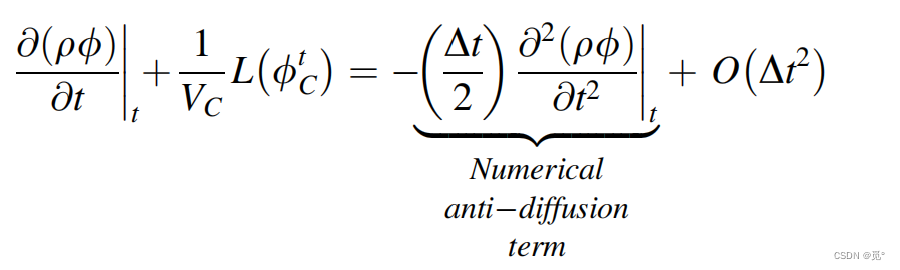
与数值反耗散相关的是数值不稳定性,且随着时间步dt的增大,数值不稳定性增强。
2)二阶瞬态欧拉格式
二阶瞬态格式同样可以采用线性插值型线构造,i.e., 可以利用对称线性型线(中心差分)构造出Crank-Nicolson (CN)格式或利用考虑远上游单元的线性插值型线构造出Adams-Moulton格式,该格式也被称为二阶迎风欧拉格式(SOUE)。
a. CN格式(中心差分型线)
当时间步均匀时,界面上参数值可以表达为
代入离散方程中,有
![]()

该格式由t-dt和t时间步参数值求解t+dt时间步参数值,为显式方法,需要CFL数限制时间步长以保证格式的稳定性。
现分析CN格式的数值精度,将t+dt和t-dt参数对t参数进行泰勒展开

代入离散方程![]() 中,有
中,有
可见该格式为二阶精度(书上截断误差给的是dt^3,有问题?)。
b. 二阶迎风欧拉格式(SOUE)
二阶迎风格式:
其中C为界面上游,U为界面远上游单元。因此
代入离散方程中,有
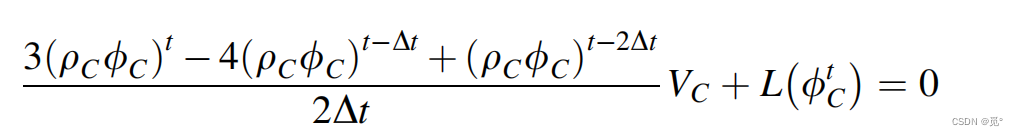
已知t-2dt和t-dt参数,通过上函数式求解t时刻参数,为隐式格式
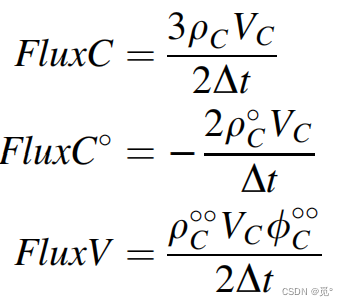
现分析SOUE格式的数值精度。将t-dt和t-2dt参数对t参数做泰勒展开:

代入离散方程中


因此SOUE格式为二阶精度格式。
2. 初始条件
采用以下时间离散“网格”

一阶迎风格式决定了

3. 非均匀时间步长
在实际应用中常采用变时间步长,在大的时间步长不能违反CFL条件。CFL条件:Courant等人最先发展了CFL条件,根据符号相反原则,要求
例如对于一维对流问题,离散方程系数为
等价于
对流问题CFL为
因此一维对流问题CFL应小于等于1。
有限体积法的非均匀时间步:时间单元定义为,两个相邻瞬态单元的时间步长为
,对于均匀时间步长有
,对于非均匀时间步长,
。

以CN格式和SOUE格式为例说明非均匀时间步长的应用方法。
1)CN格式
均匀网格时,CN格式为
非均匀网格时,上一时间步和当前时间步的参数值都会影响格式插值型线,如
代入离散方程
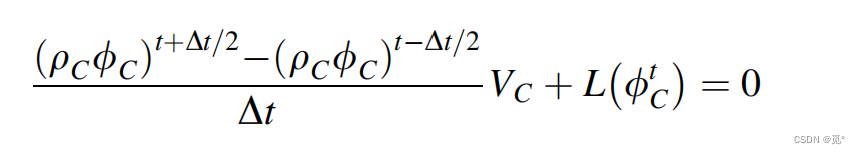
得到

2)SOUE格式



























 951
951

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








