一、欧几里得相似度
1、欧几里得相似度
公式如下所示:
 2、自定义代码实现
2、自定义代码实现
import numpy as np
def EuclideanDistance(x, y):
import numpy as np
x = np.array(x)
y = np.array(y)
return np.sqrt(np.sum(np.square(x-y)))
# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])
euclidean_distance = EuclideanDistance(x, y)
print(f"euclidean distance is: {euclidean_distance}")二、皮尔森相关性系数
1、皮尔森相关性系数
相关系数:考察两个事物(在数据里我们称之为变量)之间的相关程度。
公式如下所示:



如果有两个变量:X、Y,最终计算出的相关系数的含义可以有如下理解:
(1)、当相关系数为0时,X和Y两变量无关系。
(2)、当X的值增大(减小),Y值增大(减小),两个变量为正相关,相关系数在0.00与1.00之间。
(3)、当X的值增大(减小),Y值减小(增大),两个变量为负相关,相关系数在-1.00与0.00之间。
相关系数的绝对值越大,相关性越强,相关系数越接近于1或-1,相关度越强,相关系数越接近于0,相关度越弱。
通常情况下通过以下取值范围判断变量的相关强度:
相关系数 0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关
2、代码实现过程
自定义实现过程
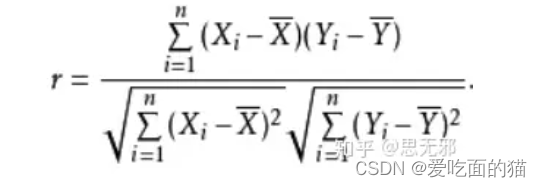
import numpy as np
def pearson_correlation(x, y):
n = len(x)
# 计算平均值
x_bar = np.sum(x) / n
# y_bar = np.sum(y) / n
# 计算协方差
cov_xy = np.sum((x - x_bar) * (y - y_bar))
# 计算标准差
std_dev_x = np.sqrt(np.sum((x - x_bar) ** 2) / (n - 1))
std_dev_y = np.sqrt(np.sum((y - y_bar) ** 2) / (n - 1))
# 计算皮尔逊相似系数
r = cov_xy / (std_dev_x * std_dev_y)
return r
# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])
# 计算皮尔逊相似系数
pearson_coefficient = pearson_correlation(x, y)
print(f"Pearson correlation coefficient: {pearson_coefficient}")numpy中的corrcpef()封装实现
import numpy as np
# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x=np.array([3.3,6.5,2.8,3.4,5.5])
y=np.array([3.5,5.8,3.1,3.6,5.1])
pc=np.corrcoef(x,y)
print(pc)3、适用范围
当两个变量的标准差都不为零时,相关系数才有定义,皮尔逊相关系数适用于:
(1)、两个变量之间是线性关系,都是连续数据。
(2)、两个变量的总体是正态分布,或接近正态的单峰分布。
(3)、两个变量的观测值是成对的,每对观测值之间相互独立。
三、余弦相似度
1、余弦相似度
公式如下所示:
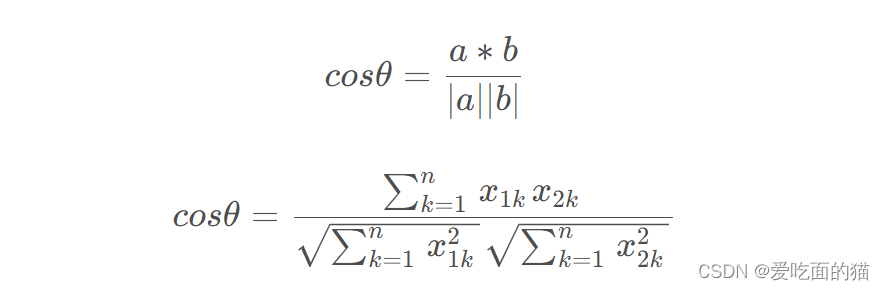
2、自定义代码实现
import numpy as np
def moreCos(a,b):
sum_fenzi = 0.0
sum_fenmu_1,sum_fenmu_2 = 0,0
for i in range(len(a)):
sum_fenzi += a[i]*b[i]
sum_fenmu_1 += a[i]**2
sum_fenmu_2 += b[i]**2
return sum_fenzi/(np.sqrt(sum_fenmu_1) * np.sqrt(sum_fenmu_2) )
# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])
cos = moreCos(x, y)
print(f"cos is: {cos}")四、曼哈顿相似度
1、曼哈顿相似度
公式如下所示:
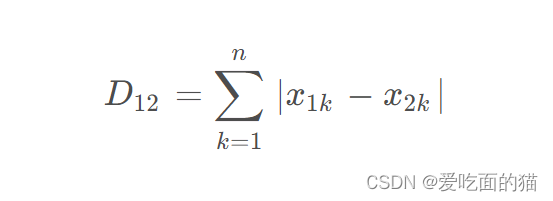
2、自定义代码实现
import numpy as np
def ManhattanDistance(x, y):
import numpy as np
x = np.array(x)
y = np.array(y)
return np.sum(np.abs(x-y))
# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])
manhattan_distance = ManhattanDistance(x, y)
print(f"manhattan distance is: {manhattan_distance}")五、切比雪夫距离
1、切比雪夫距离
公式如下所示:
切比雪夫距离(Chebyshev Distance)的定义为:max( | x2-x1 | , |y2-y1 | , … ), 切比雪夫距离用的时候数据的维度必须是三个以上。
2、自定义代码实现
import numpy as np
def ChebyshevDistance(x, y):
import numpy as np
x = np.array(x)
y = np.array(y)
return np.max(np.abs(x-y))
# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])
chebyshev_istance = ChebyshevDistance(x, y)
print(f"manhattan distance is: {chebyshev_istance}")六、马氏距离
1、马氏距离
公式如下所示:
M个样本向量X1~Xm,协方差矩阵记为S,均值记为向量μ,则其中样本向量X到u的马氏距离表示为
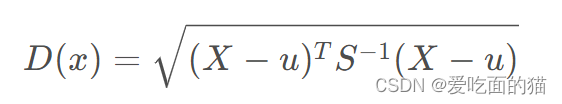
2、自定义代码实现
def MahalanobisDistance(x, y):
'''
马氏居立中的(x,y)与欧几里得距离的(x,y)不同,欧几里得距离中的(x,y)指2个样本,每个样本的维数为x或y的维数;这里的(x,y)指向量是2维的,样本个数为x或y的维数,若要计算n维变量间的马氏距离则需要改变输入的参数如(x,y,z)为3维变量。
'''
import numpy as np
x = np.array(x)
y = np.array(y)
X = np.vstack([x, y])
X_T = X.T
sigma = np.cov(X)
sigma_inverse = np.linalg.inv(sigma)
d1 = []
for i in range(0, X_T.shape[0]):
for j in range(i + 1, X_T.shape[0]):
delta = X_T[i] - X_T[j]
d = np.sqrt(np.dot(np.dot(delta, sigma_inverse), delta.T))
d1.append(d)
return d1
# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3,6.5,2.8,3.4,5.5])
y = np.array([3.5,5.8,3.1,3.6,5.1])
mahalanobis_istance = MahalanobisDistance(x, y)
print(f"mahalanobis distance is: {mahalanobis_istance}")七、闵可夫斯基距离
1、闵可夫斯基距离
公式如下所示:

当p=1时,就是曼哈顿距离
当p=2时,就是欧氏距离
当p→∞时,就是切比雪夫距离
2、自定义代码实现
import numpy as np
def MinkowskiDistance(x, y, p):
import math
import numpy as np
zipped_coordinate = zip(x, y)
return math.pow(np.sum([math.pow(np.abs(i[0] - i[1]), p) for i in zipped_coordinate]), 1 / p)
# 示例数据
# 用户1 的A B C D E商品数据 [3.3,6.5,2.8,3.4,5.5]
# 用户2 的A B C D E商品数据 [3.5,5.8,3.1,3.6,5.1]
x = np.array([3.3, 6.5, 2.8, 3.4, 5.5])
y = np.array([3.5, 5.8, 3.1, 3.6, 5.1])
# minkowski_istance = MinkowskiDistance(x, y,1)
# minkowski_istance = MinkowskiDistance(x, y,2)
minkowski_istance = MinkowskiDistance(x, y,3)
print(f"minkowski_ distance is: {minkowski_istance}")
八、信息熵
1、 信息熵
衡量分布的混乱程度或分散程度的一种度量.
熵的值就越大,样本一致性越低,越代表分之样本种类越多,越混乱,不确定性越强。
熵的值就越小,样本一致性越高,样本越倾向于某一类。
熵的值就为0,代表样本完全属于同一类。
公式如下所示:

2、自定义代码实现
import numpy as np
# 示例数据
data=np.array(['a','b','c','a','a','b'])
data1=np.array(['中国','中国','中国','中国','中国','中国','中国','中国','人民',])
#计算信息熵的方法
def calc_ent(x):
"""
calculate shanno ent of x
"""
x_value_list = set([x[i] for i in range(x.shape[0])])
ent = 0.0
for x_value in x_value_list:
p = float(x[x == x_value].shape[0]) / x.shape[0]
logp = np.log2(p)
ent -= p * logp
return ent
ent = calc_ent(data)
ent1= calc_ent(data1)
print(f"ent is: {ent}")
print(f"ent is: {ent1}")







 本文详细介绍了欧几里得距离、皮尔森相关系数、余弦相似度、曼哈顿距离、切比雪夫距离、马氏距离以及闵可夫斯基距离的计算方法,并通过Python代码示例展示了如何在实际场景中应用这些统计学上的相似度衡量手段。信息熵也被提及,作为衡量数据混乱程度的指标。
本文详细介绍了欧几里得距离、皮尔森相关系数、余弦相似度、曼哈顿距离、切比雪夫距离、马氏距离以及闵可夫斯基距离的计算方法,并通过Python代码示例展示了如何在实际场景中应用这些统计学上的相似度衡量手段。信息熵也被提及,作为衡量数据混乱程度的指标。
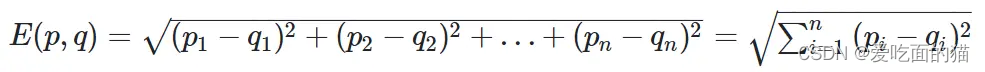

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








