深度学习笔记（十三）---多分类任务中的softmax以及各激活函数的适用场景

本文链接：https://blog.csdn.net/qq_41997920/article/details/89175595

1.5 为什么使用softmax进行归一化

参考文献：

[1] softmax的多分类

[2] 详解sigmoid与softmax，多分类及多标签分类

[3] 神经网络多分类中为什么用softmax函数归一化而不用其它归一化方法

[4] Softmax函数的特点和作用是什么？

[5] 多类分类下为什么用softmax而不是用其他归一化方法?

1.多分类任务中的softmax

1.1关于多分类

我们常见的逻辑回归、SVM等常用于解决二分类问题，对于多分类问题，比如识别手写数字，它就需要10个分类，同样也可以用逻辑回归或SVM，只是需要多个二分类来组成多分类，但这里讨论另外一种方式来解决多分类——softmax。

用于多重分类逻辑回归模型。
在构建神经网络中，在不同的层使用softmax函数。

只有用softmax才能得到每个类的概率。

softmax函数为：

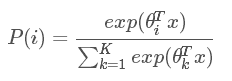
可以看到它有多个值，所有值加起来刚好等于1，每个输出都映射到了0到1区间，可以看成是概率问题。

为多个输入，训练其实就是为了逼近最佳的。

1.2 如何多分类

从下图看，神经网络中包含了输入层，然后通过两个特征层处理，最后通过softmax分析器就能得到不同条件下的概率，这里需要分成三个类别，最终会得到y=0、y=1、y=2的概率值。

三个输入通过softmax后得到一个数组[0.05 , 0.10 , 0.85]，这就是soft的功能。

计算过程直接看下图，其中即为，三个输入的值分别为3、1、-3，的值为20、2.7、0.05，再分别除以累加和得到最终的概率值，0.88、0.12、0。

1.3 代价函数

1.4 使用场景

在多分类场景中可以用softmax也可以用多个二分类器组合成多分类，比如多个逻辑分类器或SVM分类器等等。该使用softmax还是组合分类器，主要看分类的类别是否互斥，如果互斥则用softmax，如果不是互斥的则使用组合分类器。

1.5 为什么使用softmax进行归一化

原因之一在于softmax设计的初衷，是希望特征对概率的影响是乘性的。
原因之二在于，多类分类问题的目标函数常常选为cross-entropy，即 $L = -\sum_k t_k \log P(y = k)$ ，其中目标类的等于1，其它类的等于0。在神经网络模型（最简单的logistic regression也可看成没有隐含层的神经网络）中，输出层第个神经元的输入为 $a_i = \sum_d w_{id}x_d$ 。

神经网络是用error back-propagation训练的，这个过程中有一个关键的量是 $\partial L / \partial a_i$ 。
可以算出，同时使用softmax和cross-entropy时， $\partial L / \partial a_i = P(y=i) - t_i$ 。
这个形式非常简洁，而且与线性回归（采用最小均方误差目标函数）、两类分类（采用cross-entropy目标函数）时的形式一致。

2 .激活函数

概念：

饱和

当一个激活函数h(x)满足 limn→+∞h′(x)=0时，我们称之为右饱和。
当一个激活函数h(x)满足 limn→−∞h′(x)=0时，我们称之为左饱和。
当一个激活函数，既满足左饱和又满足又饱和时，我们称之为饱和。

硬饱和与软饱和

对任意的x，如果存在常数c，当 x > c 时恒有 h′(x)=0h′(x)=0 则称其为右硬饱和。
对任意的x，如果存在常数c，当 x < c 时恒有 h′(x)=0h′(x)=0 则称其为左硬饱和。
若既满足左硬饱和，又满足右硬饱和，则称这种激活函数为硬饱和。
如果只有在极限状态下偏导数等于0的函数，称之为软饱和。

2.1.什么是激活函数？

激活函数可以理解为时一种非线性转化，在神经元对输入加权求和之后，再经过一个函数计算后输出。这个函数就是激活函数。并非所有的函数都可以作为激活函数的，激活函数需要满足以下几点性质：

非线性：当激活函数是非线性函数时，一个两层的神经网络就可以去逼近绝大多数函数了。但是如果激活函数是线性的话，我们的网络始终只能学习出线性的关系出来。而无法去学习出复杂的非线性关系。
单调性：在激活函数是单调的时，我们可以保证单层网络是凸的。
可微性：在我们使用基于梯度的优化方法时，我们需要要求我们的激活函数是可微的。因为在反向传播更新梯度时，我们需要求损失函数对权重的偏导数。因此此时要求我们的激活函数是可微的。

2.2. 为什么要使用激活函数？

前面已经提到了，如果我们不使用激活函数，那么我们的网络永远都是输入的一个线性加权的组合，无法去模拟非线性的关系。这样网络的能力就受到限制。如果使用了非线性的激活函数，仅仅需要两层网络，我们就可以模拟大部分的非线性的关系了。因此，激活函数的在神经网络中起到了至关重要的作用。

2.3. 常用的激活函数有哪些？

2.3.1 sigmoid函数

饱和性：观察sigmoid函数的图像，我们可以看出在函数的两端处，也就是输出接近0或者输出接近1的地方，图像十分平缓，在这些区域sigmoid函数的梯度接近于0。这会导致一个什么问题呢？在网络进行反向传播时，会涉及到激活函数的导数，当我们样本输出在接近0或1的区域时，此时梯度式接近于0的，而当面对深度神经网络时，多个接近于0的梯度相乘会产生梯度消失的现象，这会导致我们训练可能不收敛。因此我们在使用sigmoid函数作为激活函数时，要当心初始化。一旦初始化得不好，我们的模型可能收敛的很慢甚至不收敛。
sigmoid函数的复杂性：由于sigmoid函数涉及到除法和指数计算，在我们网络正向传播是指数运算计算复杂，而在反向传播时，除法求导较为复杂。
输出空间的非对称性：可以看到，sigmoid函数的输出域为[0,1]，它不是关于0对称的。这会导致一个什么问题呢？当我们的输入如果全是正数时，我们在反向传播时，下降的梯度也是正数；当我们输入全是负数时，我们反向传播时，下降的梯度也时负数。因此会导致梯度更新权重是按照z字型下降的。但是这个问题我们可以一次训练一个batch的数据，这样就可以避免输入全是正数或者负数的现象。

那sigmoid激活函数在特征相差比较复杂或是相差不是特别大时，使用sigmoid效果比较好。

最后总结一下 Sigmoid 函数的优缺点：

优点：

Sigmoid 函数的输出映射在(0,1)之间，单调连续，输出范围有限，优化稳定，可以用作输出层。
它在物理意义上最为接近生物神经元。求导容易。

缺点：

由于其软饱和性，容易产生梯度消失，导致训练出现问题。
其输出并不是以0为中心的。

2.3.2 tanh函数

tanh函数可以看成是sigmoid函数的变形，tanh函数相比于sigmoid函数来说，它是关于原点对称的了。但是还是会存在着计算复杂，以及梯度消失的问题。tanh函数在特征相差明显时的效果会很好，在循环过程中会不断扩大特征效果。

优点：

比Sigmoid函数收敛速度更快。
相比Sigmoid函数，其输出以0为中心。

缺点：

还是没有改变Sigmoid函数的最大问题——由于饱和性产生的梯度消失。

2.3.3 ReLu函数

ReLu函数的一些性质：

在输入大于0时，此时激活函数的导数恒等于1，因此不会出现饱和的现象。但是在输入小于0时，此时为硬饱和。
ReLu是线性的，它只用将神经元的输出与某个阈值做比较，如果大于阈值，则输出神经元的输出，否则输出为0。因此无论是在正向传播还是反向传播的计算中都十分便捷。
ReLu在训练的过程中会造成神经元的死亡。为什么会造成这种情况呢？举个例子：当在反向传播时，如果此时流进网络的梯度很大，如果权重系数被更新成很大的负数后，此时很多输入经过该神经元输出都会是0。此时就落入了硬饱和区域了。而这个神经元的梯度将一直都是0。要解决这个问题就是要在设置学习率的时候，尽量不要设置太大的学习率，这样可以有效的避免神经元的失活

优点：

相比起Sigmoid和tanh，ReLU在SGD中能够快速收敛。据称，这是因为它线性、非饱和的形式。
Sigmoid和tanh涉及了很多很expensive的操作（比如指数），ReLU可以更加简单的实现。
有效缓解了梯度消失的问题。
在没有无监督预训练的时候也能有较好的表现。
提供了神经网络的稀疏表达能力。

缺点：

随着训练的进行，可能会出现神经元死亡，权重无法更新的情况。
如果发生这种情况，那么流经神经元的梯度从这一点开始将永远是0。也就是说，ReLU神经元在训练中不可逆地死亡了。

2.3.4 激活函数的选择

对于激活函数的选用，可以根据神经网络的用途及其场景，再加上对于激活函数的值域的了解，大致可以选定适合对应用途以及场景的激活函数例如，对于分类器，最终输出的是输入样本，在某一类上的可能性（概率），而概率值一般在[0,1]之间，因而最后一层输出的时候，可以选用值域在[0,1]之间的激活函数，比如说sigmoid函数。诸如此类的问题，可以根据值域来选择激活函数的运用