雷达原理（一）：雷达波形

雷达原理（一）：雷达波形

写在前面的话：
  这个系列主要学习雷达的相关原理和其$matlab$实现。
  参考书籍：《雷达系统设计$matlab$仿真》

1.低通，带通信号和正交分量

  如果信号包含的主要频率处于包括直流$(DC)$在内的低频频带,则称其为低通$(LP)$信号。如果信号包含的主要频率处于离开原点的某个频率附近,则称其为带通$(BP)$信号。一个实带通信号$x(t)$在数学上可表示为:

$x(t)=r(t)cos(2\pi f_{0}t+{\varphi }_x(t))$

其中，$r(t)$是幅度调制或包络，${\varphi }_x(t)$是相位调制，$f_0$是载波频率，$r(t)$和${\varphi }_x(t)$所含的频率成分都比$f_0$显然要小，调制频率为：

$f_m(t)=\frac{1}{2\pi }\frac{d}{dt}{\varphi }_x(t)$

瞬时频率为：

$f_i(t)=\frac{1}{2\pi }\frac{d}{dt}(2\pi f_{0}t+{\varphi }_x(t))=f_0+f_m$

如果信号带宽为$B$，且$f_0$远大于$B$，则信号$x(t)$被称为窄带信号。
带通信号也可以用两个称为正交分量的低通信号表示，此时实带通信号可表示为：

$x(t)=x_I(t)cos2\pi f_{0}t-x_Q(t)sin2\pi f_{0}t$

其中，$x_I(t)和x_Q(t)$是称为正交分量的实低通信号，分别表示为：

$x_I(t)=r(t)cos{\varphi }_x(t)$ $x_Q(t)=r(t)sin{\varphi }_x(t)$

下图说明了正交分量是如何被提取的：

2.解析信号

 在上式中定义的正弦信号$x(t)$可以写为复信号的实部，更具体地可以表示为：

$x(t)=Re${ $\psi (t)$}= $Re${ $r(t)e^{j{\varphi }_x(t)e^{j2\pi f_{o}t}}$}

定义解析信号为：

$\psi (t)=v(t)e^{j2\pi f_0(t)}$

其中

$v(t)=r(t{)}^{j{\varphi }_x(t)}$

并且

$$\Psi (\omega )=\{\begin{array}{c}2X(\omega )\omega ⩾0\\ 0\omega <0\end{array}$$

$\Psi (\omega )$是$\psi (t)$的傅里叶变换，$X(\omega )$是$x(t)$的傅里叶变换。上式可以写为

$\Psi (\omega )=2U(\omega )X(\omega )$

其中，$U(\omega )$为频域阶跃函数。由此可以得出$\psi (t)=x(t)+j\tilde{x}(t)$ ，$\tilde{x}(t)$是$x(t)$的希尔伯特变换。
\quad \quad 综合上面的式子，可以得到

$x(t)=u_{0I}(t)cos{w}_{0}t-u_{0Q}(t)sin{w}_{0}t$

\quad 这与前面推导得到的

$x(t)=x_I(t)cos2\pi f_{0}t-x_Q(t)sin2\pi f_{0}t$

是一致的，$\omega =2\pi f_0$。由帕塞瓦尔定理，可以看出$x(t)$的能量为$\psi (t)$的一半。

3.连续和脉冲波形

\quad 一个给定信号的频谱描述了其能量在频域的分布。一个能量信号(有限能量)的特征可以由它的能量谱密度($ESD$)函数来表示,而一个功率信号(有限功率)的特征可以由它的功率谱密度($PSD$)函数来表示。$ESD$的单位为$J/H$,$PSD$的单位为$W/H$。
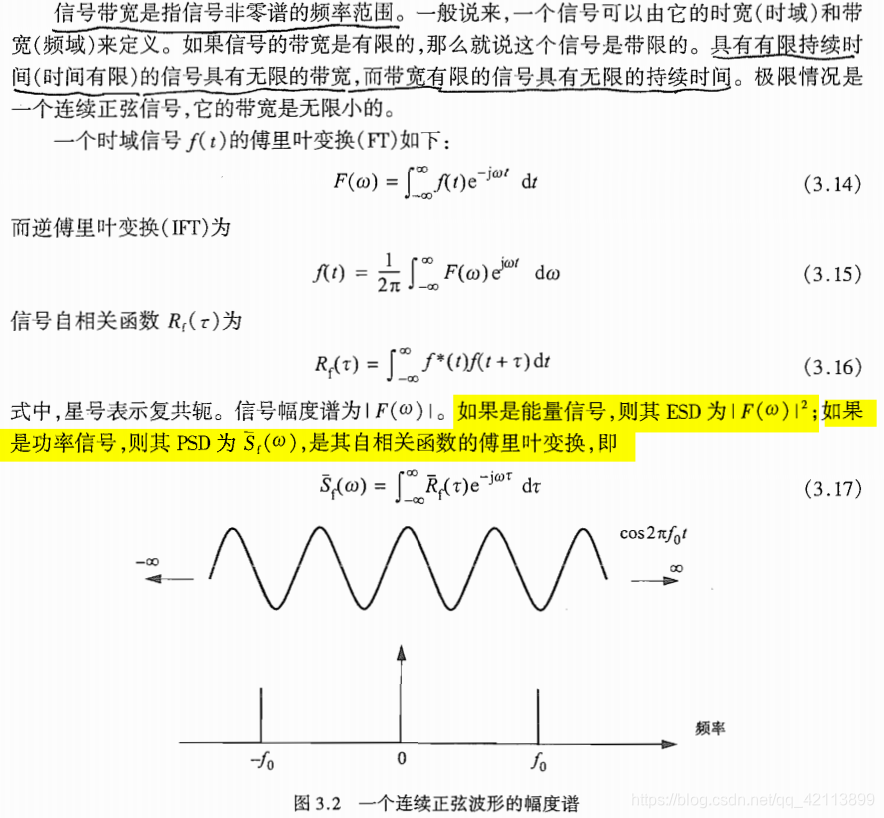
\quad 信号带宽是指信号非零谱的频率范围。一般说来,一个信号可以由它的时宽(时域)和带宽(频域)来定义。如果信号的带宽是有限的,那么就说这个信号是带限的。具有有限持续时间(时间有限)的信号具有无限的带宽,而带宽有限的信号具有无限的持续时间。极限情况是一个连续正弦信号,它的带宽是无限小的。

4.线性调频波形

下面的重点是研究线性调频信号的matlab实现

function LFM(B,T);
time_B_product = B * T;
if(time_B_product < 5 )
    fprintf('************ Time Bandwidth product is TOO SMALL ***************')
    fprintf('\n Change B and or T')
    return
else
end
% Compute alpha
mu = 2. * pi * B / T;
npoints = 5 * B * T + 1;
% Determine sampling times
delt = linspace(-T/2., T/2., npoints); % 
% Compute the complex LFM representation
Ichannal = cos(mu .* delt.^2 / 2.); % Real part
Qchannal = sin(mu .* delt.^2 / 2.); % Imaginary Part
LFM = Ichannal + sqrt(-1) .* Qchannal; % complex signal
%Compute the FFT of the LFM waveform
LFMFFT = fftshift(fft(LFM));
% Plot the real and Inginary parts and the spectrum
sampling_interval = T / npoints;
freqlimit = 0.5 / sampling_interval;
freq = linspace(-freqlimit,freqlimit,npoints);
figure(1)
plot(delt,Ichannal,'k');
axis([-T/2 T/2 -1 1])
grid



xlabel('Time - seconds')
ylabel('Units of Waveform')
title('Real part of an LFM waveform')
figure(2)
plot(delt,Qchannal,'k');
axis([-T/2 T/2 -1 1])
grid



xlabel('Time - seconds')
ylabel('Units of Waveform')
title('Imaginary part of LFM waveform')
figure(3)
plot(freq, abs(LFMFFT),'k');
%axis tight
grid
xlabel('Frequency - Hz')
ylabel('Amplitude spectrum')
title('Spectrum for an LFM waveform')

\quad 此函数传入的参数为未压缩的脉宽$T$和调制带宽B

5. 高距离分辨率

\quad\quad 距离分辨率

$\Delta R=\frac{c\tau }{2}=\frac{c}{2B}$

\quad\quad 雷达使用者和设计者不约而同地通过最小化$\Delta R$来寻求实现高距离分辨率$(HRR)$。然而如式(3.47)所示,为了得到高距离分辨率,必须使用短脉冲,从而导致平均发射功率的减小,并且强加了对大工作带宽的需求。在得到好的距离分辨率的同时保持足够的平均发射功率,可以通过使用脉冲压缩技术来实现,。利用频率或相位调制,脉冲压缩可以使我们获得相当长脉冲的平均发射功率,同时得到对应非常短脉冲的距离分辨率。例如,考虑一个$LFM$波形,其带宽为B,未压缩脉宽为$\tau$。经过脉冲压缩后,压缩后的脉宽表示为${\tau }^{{}^{\prime }}$ ，其中${\tau }^{{}^{\prime }}$<<$\tau$ , $HRR$为

$\Delta R=\frac{c{\tau }^{{}^{\prime }}}{2}<<\frac{c{\tau }^{}}{2}$

\quad \quad 常用方法是使用线性调频和调频(FM)连续波信号来得到$HRR$。

6.其他波形以后待补充（接着这篇文章添加）