1,一阶逻辑系统 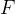
1.1,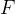 的定义
的定义
一阶逻辑系统也称为谓词系统或者量化理论。一阶形式系统可写为
,其中:
的通用逻辑符号包括:连接词(
),量词(
),辅助符号(
)。非逻辑符号包括:可数无穷多个个体/函数/命题/谓词变元。任意多个个体/函数/命题/谓词常元。
可归纳定义如下:(1)若
为个体变元或常元,则
;(2)若
为
元函数常元或变元,
为项,则
为项;(3)任何项都可有限次应用(1)和(2)获得。
由下列公式构成:设
为
元谓词常元或者变元,
为项,则
。
可归纳定义如下:(1)
;(2)若
则
;(3)若
则
;(4)若
且
是个体变元,则
;(5)任何公式都可有限次应用规则(1)-(4)构造得到。
将
称为
语言,记为
。
1.2,自由/约束出现
设
为个体变元:
- 称
在
中形如
或者
的子公式的出现称为约束出现。
- 变元的非约束的出现称为自由出现。
- 若
在
中有约束出现,则称
为约束变元。
- 若
在
中有自由出现,则称
为自由变元。
- 若
中无自由的个体,则称
为闭公式。可能包括函数变元、命题变元、谓词变元。
- 若
中除约束个体变元外无其他变元,则称
为句子。
1.3,代入操作
个体变元代入(对项的代入):设
是个体变元,
是项,令
:
- 若
为个体常元,则
;
- 若
为个体变元,则
;
- 若
为函数常元,则
;
- 若
为函数变元,则
;
个体变元代入(对公式的代入):设
是个体变元,
是项,令
:
- 对原子公式
,有
;
;
;
;
命题变元代入(对公式的代入):设
是命题变元,
是公式,令
:
;
,
为
元谓词常元或者变元,不包含命题变元,不进行替换。
;
;
。
1.4,可代入(自由)
项的可代入:称项
对公式
中的个体变元
可代入(为自由的),如果对
中的每个变元
,变元
在
辖域内无自由出现。
公式的可代入:称公式
对
中的命题变元
可代入(为自由的),如果对
中的每个自由变元
而言,
不出现在
辖域内。
原则:代入前后约束出现的次数不改变。
1.5,公理集和规则集
公理集:
,其中项
对
中的
是自由的。
,其中
在
中无自有出现。
规则集:
2,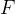 的定理与导出规则
的定理与导出规则
2.1,无/有前提依赖证明
一阶系统有两类证明方式:无前提依赖与有前提依赖。
- 无前提依赖:不使用公设集中的公式,证明序列中仅出现公理以及通过应用规则得到的公式。
- 带前提依赖:证明序列中可能包含公设集中的公式。
在前提依赖证明中,对
规则增加了相应限制,并且还需要一条额外的
规则。同时,还要区分公设集为有穷和无穷情况。
2.2,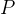 永真及P规则
永真及P规则
称
是
永真的,如果存在
中的永真式
以及命题变元代入
使得
。
P-规则:
- 若
是
中的永真式,则
;
是
的公式。
- 若
是
永真的,则
;
是
的公式。
- 若
且
是
永真的,则
。
2.3,无前提依赖证明的协调性
取
,定义映射
如下:
- 若
,则
。
若
则
关于无前提依赖证明满足绝对协调及关于否定协调。
2.4,肯定出现及否定出现
设
,并将
中的派生连接词、量词全部用原始符号
替换,则:
- 若
在
中的某个指定出现位置位于偶数个
的辖域中,则称
的该次出现为正出现或者肯定的。
- 若
在
中的某个指定出现位置位于奇数个
的辖域中,则称
的该次出现为负出现或者否定的。
- 若
在
中的所有指定出现都是肯定的,则称
在
中为肯定的。
- 若
在
中的所有指定出现都是否定的,则称
在
中为否定的。
:设
,且
为出现在
和
中的所有自由个体变元,则:
- 若
在
中为肯定的,则
。
- 若
在
中为否定的,则
。
- 若
在
中为肯定的,且
,则
。
- 若
在
中为否定的,且
,则
。
:设
,且
为出现在
和
中的所有自由个体变元,则:
。
- 若
,则
。
- 若
且
,则
。
证明:令
为用
替换
在
中所有肯定出现所得之公式;于是
必然是用
替换
在
中否定出现所得之公式。利用
,可得
及
。
2.5,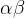 条件
条件
设
,
不是
的自由变元且
对
中的
为自由的,则称
和
关于
满足
条件,记作:
。
- 带入可逆性:
- 换名等价性:
规则:若
,则
- 若
对
中的
是自由的,则
- 若
,则
:若
,且
对
中的
是自由的,则
:若
且
在
中不自由,则
:若
,
,且
对
中的
是自由的,但在
中不自由,则
。
:若
,同时
,
,则
。
:若
且
则
。
2.6,带前提依赖证明
给定有穷公式集
,如果存在有穷序列
,且对每个
必有一下几种情况成立:
- Hyp:
;
- Ax:
是公理;
- MP:存在
,使得
;
- Gen:存在
,使得
,其中
在
中不自由;
:存在
,公式
,个体变元
和
满足
,且
。
则称
由
可证,记作
,并称
是由
导出
的证明。
若
是无穷集,则
是指存在
的一个有穷子集
使得
。
定理和派生规则:
:若
,且
是
永真的,则
。
:若
,
在
中是肯定的(/否定的)且
,则
。
:若
且
则
。
:若
,
在
中不自由,
对
中的
是可代入的,则
。
:若
,
在
中不出现,
对
中的
是可代入的,则
。
3,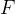 的语义及前束范式
的语义及前束范式
3.1,函数单点取代操作
设
,则任取
及
,可以得到一个新的函数
,其定义如下:
性质:
- 若
,则
。
3.2,解释和论域
给定二元偶
为
的一个解释,其中
是一个非空集合,称为论域。
为如下定义的一个映射:
- 若
为个体常元,则
;
- 若
为
元函数常元,则
;
- 若
为命题常元,则
,其中
;
- 若
为
元谓词常元,则
。
给定解释
,若映射
满足:
- 若
为个体变元,则
;
- 若
为
元函数变元,则
;
- 若
为命题变元,则
;
- 若
为
元谓词变元,则
。
则称
为
下的一个指派。用
表示
下所有指派构成的集合。
3.3,项和公式的语义
项的语义:设
以及
,对每个
,可归纳定义其语义
如下:
- 若
为个体常元,则
。
- 若
为个体变元,则
。
- 若
,其中
为
元函数常元,则
。
- 若
,其中
为
元函数变元,则
。
公式的语义:设
以及
,对每个
,可归纳定义其语义
如下:
- 若
,其中
为
元谓词常元,则
。
- 若
,其中
为
元谓词变元,则
- 若
,则
。
- 若
,则
。
- 若
,则
。
3.4,带入定理
设
,项
对
中的
可代入,公式
对
中的命题变元
可代入。则对任意解释
以及指派
:
- 对任意的项
有
,其中
。
,其中
。
,其中
。
若
在
中不自由,则对任意的
,有
。
推论:若
为句子,则
的真值只与解释有关,而与指派无关。
3.5,可满足和模型
可满足:给定公式
,若存在解释
以及
使得
,则称
是可满足的,并记作
。
模型:若对于公式
,存在解释
使得每个
都有
成立,则称
是
的模型,记作
。
永真式:若每个解释都是
的模型,就称
是永真式或者有效的。
可满足:给定公式集合
,若存在解释
以及
使得对每个
都有
,成立,则称
是可满足的,此时记作
。
模型:特别的,若对每个
都有
,就称
是
的一个模型,记作
。
逻辑结果:若对每个解释
及
,若
则
,就称
是
的逻辑结果,记作
。
3.6,前束范式
设

为个体变元:
- 若
为
的子公式,且
在
中无自有出现,则称
为空量词。
- 若
中无空量词,且量词均不出现在
的辖域内,则称
为前束范式。
因此,若
为前束范式,当且仅当
形如:
。其中
不含量词,
,
是彼此不同的个体变元。
若
满足如下条件:
无空量词;
中的自由变元与约束变元不同名;
中不同的约束变元之间不同名;
则称
是矫正的。
设
是矫正的公式,并假设其中从左到右第
个量词为
,那么
的前束范式为
。其中:
若肯定出现则不需要改变,否定改变取其对偶。
4,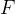 系统的元性质
系统的元性质
4.1,可靠性
可靠性定理:
- 若
则
。
- 若
则
。
推论:若公式集
是可满足的,则
必是协调的。
证明:若
不协调,则
且
。由可靠性定理,有
及
。因为
是可满足的,不妨设
,则
与
矛盾。
4.2,协调性
一阶语言分层:分别令
,为
中的全体句子、闭公式和公式构成的集合。令
为
中全体闭项(不含变元的项)构成的集合。
协调性:设
是一阶逻辑系统:
- 若
,则称
为绝对协调的。
- 若
,则
或者
,就称
关于否定协调。
- 若
,则称
是协调的。
设
,若
为协调的,则称
与
协调;否则称
与
不协调。特别的,若
为有穷集时,则把
与
(不协调)称为
与
协调(不协调)。
协调集的性质:
与
不协调当且仅当
。
推论:
与
不协调当且仅当
。
4.3,独立性
独立性:
将全称量词
的语义重新定义如下:
可以验证:除
均为永真式,
均保持永真性。但是,公理
在该解释下永真,因此
独立。
独立性:
选定某一个谓词常元
,个体变元
,以及命题常元
。令
为将
中
全部替换为
所得之公式。考虑到前提为空的情形——若
可不使用
证出,则
必然是永真式。
考虑公式
,显然有
,从而是永真式。但是
不是永真式,从而
独立
独立性:
考虑在
中有
成立,但是
中任一公里的长度均大于
的长度;
和
规则均不能减少已证定理的长度。因此
规则独立。
规则独立性:
考虑新解释
:对每个形如
的公式有
;同时对其他公司的定义不变(
)。于是,若
,则
必然是
的模型。但
不是
的模型,因此
,从而
独立。
规则独立性:
首先,
。其次,设
是在标准解释的基础上,将所有形如
的值重赋为
解释,则对任意
若
,则
必为
的模型。但是,
不是
的模型。因此
独立。
4.4,完全性
完全集:设
,若对每个
,有
或者有
,则称
是完全的。(与形式系统完全性不是一个概念)
极大协调集:若公式集
即是完全的又是协调的,则称
是极大协调集。
极大协调集性质:设
为极大协调集,则:
- 对任意公式
而言,
与
恰好有一个在
中;
- 若
,则
与
不协调。
协调集的可容许性质:设
是
上的升链,且每个
都是协的,则
也是协调的。
协调集的可扩张性:若
是协调集,则存在极大协调集
使得
。
形式系统的膨胀:设
与
是两个一阶形式系统:
- 若
,则称
是
的膨胀,记作
。
- 若
,则称
是
的真膨胀,记作
。
形式系统的扩张:设
与
是两个一阶形式系统,
:
- 若
且
,则称
为
的扩张,记作
。
- 若
(偏序),且
,则称
为
的保守扩张,记作
。
若
则
为协调的当且仅当
为协调的。
若
,且两者的差别仅有个体常元,
,则
。
节省解释和节省模型:若解释
满足
,则称
是节省的。若
的模型是节省的,则称该模型为其节省模型。
语言保势扩张:给定两个一阶形式系统
,若
且
,则
。
协调集的可满足性:若
是协调的,则必有节省解释
满足
。
完全性定理:
- 若
,则
。
- 若
,则
。
4.5,紧致性
语法紧致性:一阶逻辑公式集
是协调的当且仅当其每个有穷子集是协调的。
语义紧致性:一阶逻辑公式集
是可满足的当且仅当其每个有穷子集是可满足的。































 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










