kernel核函数是什么、用来干什么 及其详细推导

在说核函数之前,我们先说说映射及其作用.

       如果在当前空间对数据类别不好使用线性函数进行划分，则通过一个函数φ( x)将数据点从当前空间映射到另一空间去（映射后的空间叫特征空间，通常是更高维的空间，当然不是绝对）以方便使用线性函数进行分类（最高次不超过1的n元函数称为线性函数）。

      如下图中在原来的空间中需要用圆将数据分为两类，但是现在将原2维的数据分别映射到2维、3维的空间中，从而可以在映射后的2维空间中使用一条直线将数据分类，在映射后的3维空间中使用一个平面将数据分为两类。

1. 那么什么叫做核函数了？

       核函数就是特征空间中向量的内积 用 原空间对应向量 表示出来的表达式。以上面转到3维空间去为例，3维特征空间中向量φ(x)=φ(x1,x2)，φ(z)=φ(z1,z2)的内积最终可表示为<φ(x),φ(z)>=(<(x1,x2),(z1,z2)>)^2=(<x,z>)^2。(推导过程如图所示，其中向量x=(x1,x2),z=(z1,z2)是原坐标空间的向量)。表达式(<x,z>)^2就称为核函数，表示为K(x,z)=(<x,z>)^2。（向量x=(x1,x2)就表示的起点为坐标轴原点，终点为点x(x1,x2)的向量）。注意此处按这样的方式映射到3维空间后的核函数是(<x,z>)^2，但是不表示只能按这样的映射方式才能得到这个核函数(<x,z>)^2，也就是说同一个核函数可能对应多种映射方式。

核函数的作用

从此处可以看出，只要有了核函数，那么计算特征空间中向量间的内积时是否知道映射函数就不重要了，也就是说我们不用去关心数据到底是通过什么样的映射方式从原空间映射到了特征空间，也不用关心其在特征空间的坐标。

那么知道了特征空间中的内积后，我们又可以得到哪些东西了？

       我们知道向量的内积是两个向量φ(x),φ(z)是两个向量的长度和两个向量夹角的余弦的乘积，即||φ(x)||*||φ(z)||*cosΘ。所以这时我们就可以将向量之间的夹角的余弦值表示出来，即：
cosΘ=<φ(x),φ(z)>/(||φ(x)||)(||φ(z)||)。我们知道cosΘ的正负可以表示为φ(z)是偏向φ(x)的正方向一点，还是偏向φ(x)的负方向一点。而两向量的长度的乘积(||φ(x)||)(||φ(z)||)一定是正的。所以cosΘ的正负就可以用<φ(x),φ(z)>来表示。

那么重点来了，当我们知道了cosΘ的正负后，又能对我们的分类起到什么作用了？

      如果映射后类别1的中心点为m1`,类别2的中心点为m2`。m1`和m2`的中间点为m`。此时过m`且垂直于(m1`-m2`)向量的平面是不是刚好将这两个类别分开。而对于某一点φ(x)来说，向量（φ(x)-m`）和向量（m1`-m2`)的夹角Θ如果在（0，π/2)之间，即cosΘ在(0,1)之间时，其为类别1；如果两向量夹角在（π/2，π）之间，即cosΘ在(-1，0)之间时，其为类别为2。所以只要知道了向量（m1`-m2`）和向量（φ(x)-m`）的内积<( m1`-m2`),(φ(x)-m`)>就可以知道φ(x)所属于的类别了。如图（你也可以将其想象成一个超空间，此时中间的直线就是超平面了）：

 但是了，我们前面讲核函数的时候，K(x,z)的形式和当前表达式是有点区别的，那么<(m1`-m2`）,(φ(x)-m`)>我们又是否能通过核函数将其用原空间的向量的表达式将其表达出来了？见下图推导：

（这里的推导主要就是为了证明对于分类，我们只需要知道核函数，而不必知道具体的映射函数就行）

第一种推导：

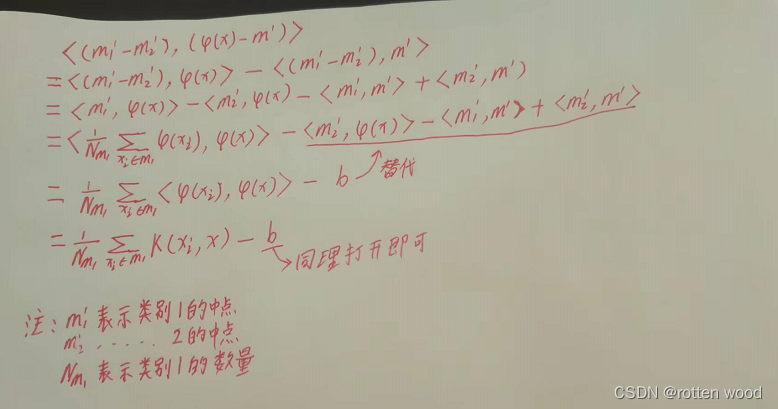
第二种推导:

所以到现在我们是不是就可以通过核函数将数据的类别判断出来了。