数字滤波器设计——MATLAB仿真篇1

下定决心从事信号处理及无线与移动通信方向后，最重要的可能还是要打好基础，加上好久也没有时间更新博客，这次权当记录一些基础的知识。

1. IIR滤波器（无限冲激响应滤波器）
   下面是MATLAB给出的一些IIR滤波器的调用方式：

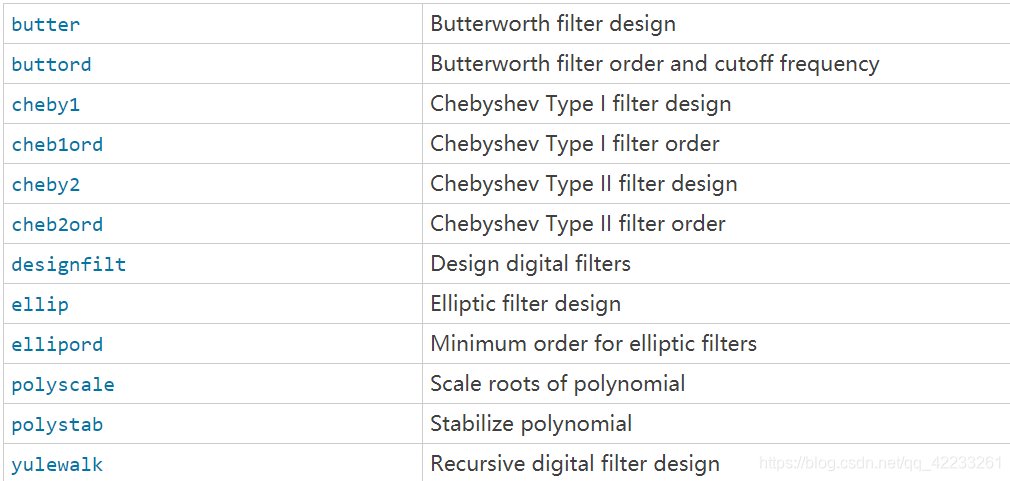
利用这些函数，我们很轻易的就能调用并且仿真出结果。下面是进行巴特沃斯低通滤波的代码：

%% 巴特沃斯低通滤波
% create by Grass
%% 滤波器参数
fs=20000;%采样频率
N=201;%采样点数
t=(0:N-1)/fs;%采样时间
%% 产生xn和hn
f1=600;
f2=2000;
x=sin(2*pi*f1*t)+sin(2*pi*f2*t);
figure;
plot(t,x);
title('叠加两个频率的输入信号'),xlabel('时间/s'),ylabel('幅度');
%巴特沃斯低通滤波器设计
Wp=f1/(fs/2); %通带截止频率
Ws=f2/(fs/2); %阻带截止频率
[n,Wn]=buttord(Wp,Ws,3,60);
[B,A]=butter(n,Wn);%调用巴特沃斯函数
%% 观察巴特沃斯函数形状
figure;
freqz(B,A);
%% 进行卷积
y=filter(B,A,x);
figure;
plot(t,y);
title('滤波之后的函数'),xlabel('时间/s'),ylabel('幅度');

得到的结果如下所示：

2. FIR滤波器（有限冲击响应滤波器）

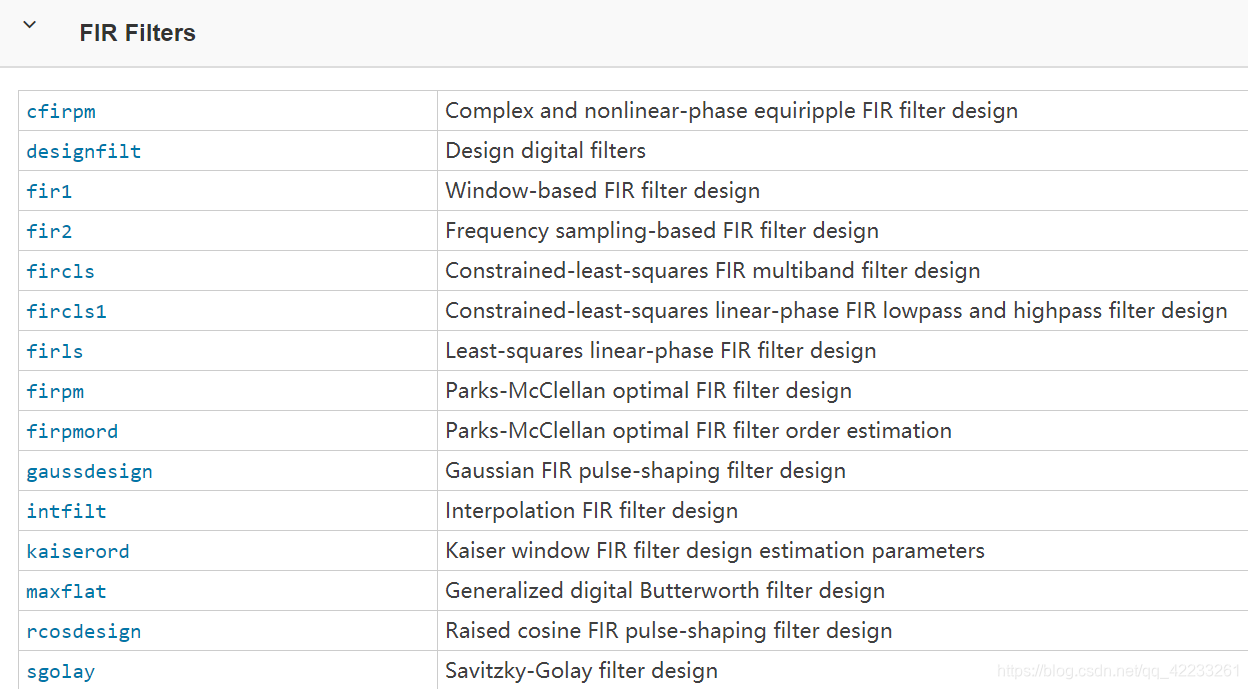
下面介绍fir2的使用方法：

b = fir2(n,f,m)

其中n为滤波器阶数，通常为整数，f是0到1的频率点的向量，其中1对应于奈奎斯特频率。f的第一个点必须是0，最后一个点必须是1。f必须按照递增的顺序排序。允许重复频率点，并将其视为频率响应中的步骤。m是一个向量，包含f中指定的每个点的期望大小响应。如果是低通滤波器，那么m=[1,1,0,0]；
使用FIR滤波的代码如下：

%% FIR滤波器设计
% create by Grass
%% 滤波器参数
fs=20000;%采样频率
N=201;%采样点数
t=(0:N-1)/fs;%采样时间
%% 产生xn和hn
f1=600;
f2=2000;
x=sin(2*pi*f1*t)+sin(2*pi*f2*t);
figure;
plot(t,x);
title('叠加两个频率的输入信号'),xlabel('时间/s'),ylabel('幅度');
%FIR滤波器设计
f=[0,f1/fs,f1/fs,1];
m=[1,1,0,0];
b1=fir2(25,f,m);
[h1,w]=freqz(b1,1);
figure;
plot(w/pi,abs(h1))
xlabel('\omega / \pi');
%% 进行卷积
y=filter(4*b1,1,x);%增益补偿
figure;
plot(t,y);
title('滤波之后的函数'),xlabel('时间/s'),ylabel('幅度');

得到的结果如下：

这次关于滤波器的学习就到此结束啦~有什么问题可以下方留言联系！下期再见！