【知识框架】

5.1 树的基本概念
5.1.1 树的定义
树是n(n>=0)个节点的有限集。当n=0时,称为空树。
在任意一棵非空树中应满足:
- 有且仅有一个特定的称为根(Root)的结点。
- 当n>1时,其余结点可分为m(m>0)个互不相交的有限集T1,T2,…Tm,其中每个集合本身又是一棵树,并称为根的子树(SubTree)。
显然,树的定义是递归的,即在树的定义中又用到了其自身,树是一种递归的数据结构。
树作为一种逻辑结构,同时也是一种分层结构,有以下两个特点:
- 树的根结点没有前驱,除根结点以外的所有结点有且只有一个前驱(n>0时,根结点是唯一的,不可能存在多个根结点)。
- 树中所有结点可以有零个或多个后继(m>0时,子树的个数没有限制,但它们一定是不相交的)。
树适合用于表示具有层次结构的数据。树中的某个结点(除根结点外)最多只和上一层的一个结点(即其父结点)有直接关系,根结点没有直接上层结点,因此在n个结点的树中有n-1条边。而树中的每个结点与其下一层的零个或多个结点(即其子女结点)有直接关系。


子树T1,T2就是根结点A的子树。
D、G、H、I组成的树又是B为结点的子树,E、J组成的树是C为结点的子树。
5.1.2 基本术语
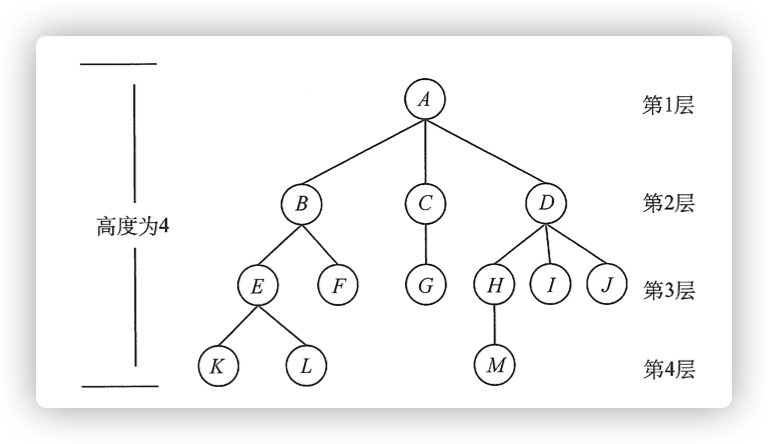
-
考虑结点 K ∘ K_{\circ} K∘ 根 A A A 到结点 K K K 的唯一路径上的任意结点,称为结点 K K K 的
祖先。如结点 B B B 是 结点 K K K 的
祖先,而结点 K K K 是结点 B B B 的子孙。路径上最接近结点 K K K 的结点 E E E 称为 K K K 的
双亲(Parent), 而 K K K 为结点 E E E 的孩子(Child)。根 A A A 是树中唯一没有双亲的结点。有相同双亲的结点称为
兄弟(Sibling),如 结点 K K K 和结点 L L L 有相同的双亲 E , E , E, 即 K K K 和 L L L 为兄弟。 -
树中一个结点的孩子个数称为该结点的
度(Degree),树中结点的最大度数称为树的度。如结点 B B B 的 度为 2,结点 D D D 的度为 3,树的度为 3。
-
度大于 0 的结点称为
分支结点(又称非终端结点);度为 0 (没有子女结点)的结点称为
叶子结点(又称终端结点)。在分支结点中,每个结点的分支数就是该结点的度。
-
结点的深度、高度和层次。
结点的层次从树根开始定义,根结点为第 1 层,它的子结点为第 2 层,以此类推。
双亲在同一层的结点互为
堂兄弟,图 中结点 G \mathrm{G} G 与 E , F , H , I , J \mathrm{E}, \mathrm{F}, \mathrm{H}, \mathrm{I}, \mathrm{J} E,F,H,I,J 互为堂兄弟。结点的深度是从根结点开始自顶向下逐层累加的。结点的高度是从叶结点开始自底向上逐层累加的。树的高度(或深度)是树中结点的最大层数。图中树的高度为 4。 -
有序树和无序树。
树中结点的各子树从左到右是有次序的,不能互换,称该树为
有序树,否则称为无序树。假设图为有序树,若将子结点位置互换,则变成一棵不同的树。
-
路径和路径长度。
树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的,而路径长度是路径上所经过的边的个数。
注意: 由于树中的分支是有向的,即从双亲指向孩子,所以树中的路径是从上向下的,
同一双亲的两个孩子之间不存在路径。 -
森林。森杜是 m ( m ≥ 0 ) m(m \geq 0) m(m≥0) 棵互不相交的树的集合。
森林的概念与树的概念十分相近,只要把树的根结点删去就成了森林。
反之,只要给 m m m 棵独立的树加上一个结点,并把 这 m m m 棵树作为该结点的子树,则森林就变成了树。
5.1.3 树的性质
树具有如下最基本的性质:
- 树中的结点数等于所有结点的度数加 1。
- 度为 m m m 的树中第 i i i 层上至多有 m i − 1 m^{i-1} mi−1 个结点 ( i ≥ 1 ) (i \geq 1) (i≥1) 。
- 高度为 h h h 的 m m m 叉树至多有 ( m h − 1 ) / ( m − 1 ) \left(m^{h}-1\right) /(m-1) (mh−1)/(m−1) 个结点。
- 具有 n n n 个结点的 m m m 叉树的最小高度为 ⌈ log m ( n ( m − 1 ) + 1 ) ⌉ \left\lceil\log _{m}(n(m-1)+1)\right\rceil ⌈logm(n(m−1)+1)⌉
( ⌈ ⌉ \left\lceil\right\rceil ⌈⌉这种上边带横的,是指不小于括号里式子的最近的整数。(注意是不小于,如果正好是整数的话,就是这个整数本身)
还有一种是下边带横的,指不大于括号里式子的最近整数。(注意是不大于,如果正好是整数的话,就是这个整数本身)
度为m的树中,有n1个度为1的节点……nm个度为m的结点,根据“树中所有结点的度数加 1 等于结点数”的结论,
有 n = ∑ i = 0 m i n i = n 1 + 2 n 2 + 3 n 3 + ⋯ + m n m + 1 n=\sum_{i=0}^{m} i n_{i}=n_{1}+2 n_{2}+3 n_{3}+\cdots+m n_{m}+1 n=∑i=0mini=n1+2n2+3n3+⋯+mnm+1 。
又有 n = n 0 + n 1 + n 2 + ⋯ + n m n=n_{0}+n_{1}+n_{2}+\cdots+n_{m} n=n0+n1+n2+⋯+nm, 所以叶子结点数n0
n 0 = ( n 1 + 2 n 2 + 3 n 3 + ⋯ + m n m + 1 ) − ( n 1 + n 2 + ⋯ + n m ) = n 2 + 2 n 3 + ⋯ + ( m − 1 ) n m + 1 = 1 + ∑ i = 2 m ( i − 1 ) n i \begin{aligned} n_{0} &=\left(n_{1}+2 n_{2}+3 n_{3}+\cdots+m n_{m}+1\right)-\left(n_{1}+n_{2}+\cdots+n_{m}\right) \\ &=n_{2}+2 n_{3}+\cdots+(m-1) n_{m}+1=1+\sum_{i=2}^{m}(i-1) n_{i} \end{aligned} n0=(n1+2n2+3n3+⋯+mnm+1)−(n1+n2+⋯+nm)=n2+2n3+⋯+(m−1)nm+1=1+i=2∑m(i−1)ni
常用于求解树结点与度之间关系的有:
(1) 总结点数 = n 0 + n 1 + n 2 + ⋯ + n m =n_{0}+n_{1}+n_{2}+\cdots+n_{m} =n0+n1+n2+⋯+nm 。
(2) 总分支数 = 1 n 1 + 2 n 2 + ⋯ + m n m ( 度为 m 的结点引出 m 条分支 ) 。 =1 n_{1}+2 n_{2}+\cdots+m n_{m}(\text { 度为 } m \text { 的结点引出 } m \text { 条分支 })_{\text {。 }} =1n1+2n2+⋯+mnm( 度为 m 的结点引出 m 条分支 )。
(3) 总结点数 = = = 总分支数 + 1 +1 +1 。
5.1.4 树的抽象数据类型
| InitTree(*T) | 构造空树T |
|---|---|
| DestroyTree(*T) | 销毁树T |
| CreateTree(*T,definition) | 按definition中给出树的定义来构造树 |
| ClearTree(*T) | 若树T存在,则将T清为空树 |
| TreeEmpty(T) | 若T为空树,返回True,否则返回False |
| TreeDepth(T) | 返回树的深度 |
| Root(T) | 返回T的根结点 |
| Value(T,cur_e) | cur_e是树T中的一个结点,返回此结点的值 |
| Assign(T,cur_e,value) | 给树T的结点cur_e赋值为value |
| Parent(T,cur_e) | 若cur_e是树T的非根结点,则返回它的双亲,否则返回空 |
| LifeChild(T,cur_e) | 若cur_e是树T的非叶结点,则返回它的最左孩子,否则返回空 |
| RightSibling(T,cur_e) | 若cur_e有右兄弟,则返回它的右兄弟,否则返回空 |
| InsertChild(*T,*p,i,c) | 其中p指向树T的某个结点,i为所指结点p的度上加1,非空树c与T不相交,操作结果为插入c为树T中p指结点的第i棵子树 |
| DeleteChild(*T,*p,i) | 其中p指向树T的某个结点,i为所指结点p的度,操作结果为删除T中p所指结点的第i棵子树 |
5.2 二叉树的概念
5.2.1 二叉树的定义及其主要特性
- 二叉树的定义
二叉树是另一种树形结构,特点是每个结点至多只能有两棵








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








