【C++】归并排序的理解-剑指offer51：计数数组中的逆序对和148：排序链表

原创

已于 2022-03-29 10:48:31 修改 · 715 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #排序算法 #算法

于 2022-02-17 14:56:55 首次发布

这篇博客介绍了归并排序的基本思想，并展示了如何利用归并排序来计算数组中的逆序对数量以及对链表进行排序。在计算逆序对时，通过比较归并过程中元素的大小关系，动态统计逆序对数量。对于链表排序，通过两次递归调用归并排序分别处理链表的左右部分，然后使用归并操作将已排序的子链表合并。此外，还提到了链表排序的快速排序版本。

归并排序的理解-解决数组中的逆序对问题

0x00 归并排序的基本思想：

归并排序（MERGE-SORT）是利用归并的思想实现的排序方法，该算法采用经典的分治（divide-and-conquer）策略（分治法将问题分(divide)成一些小的问题然后递归求解，而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起，即分而治之)。其过程展示图如下(这里以数组[8, 4, 5, 7, 1, 3, 6, 2]为例子)：
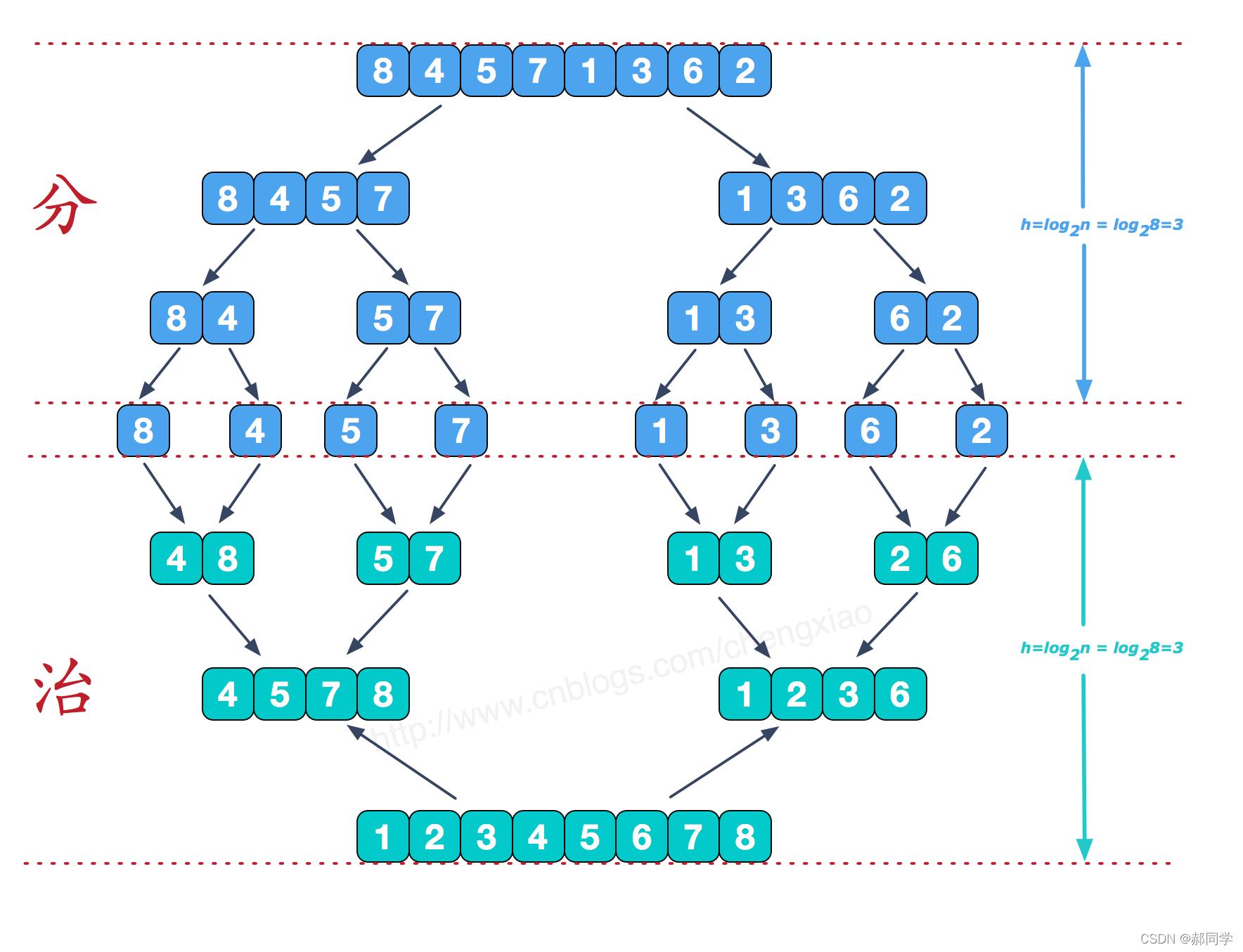
在这里插入图片描述
最后一部分的“治”的详细过程如下，即[4,5,7,8] 与 [1,2,3,6] 二者之间的合并；

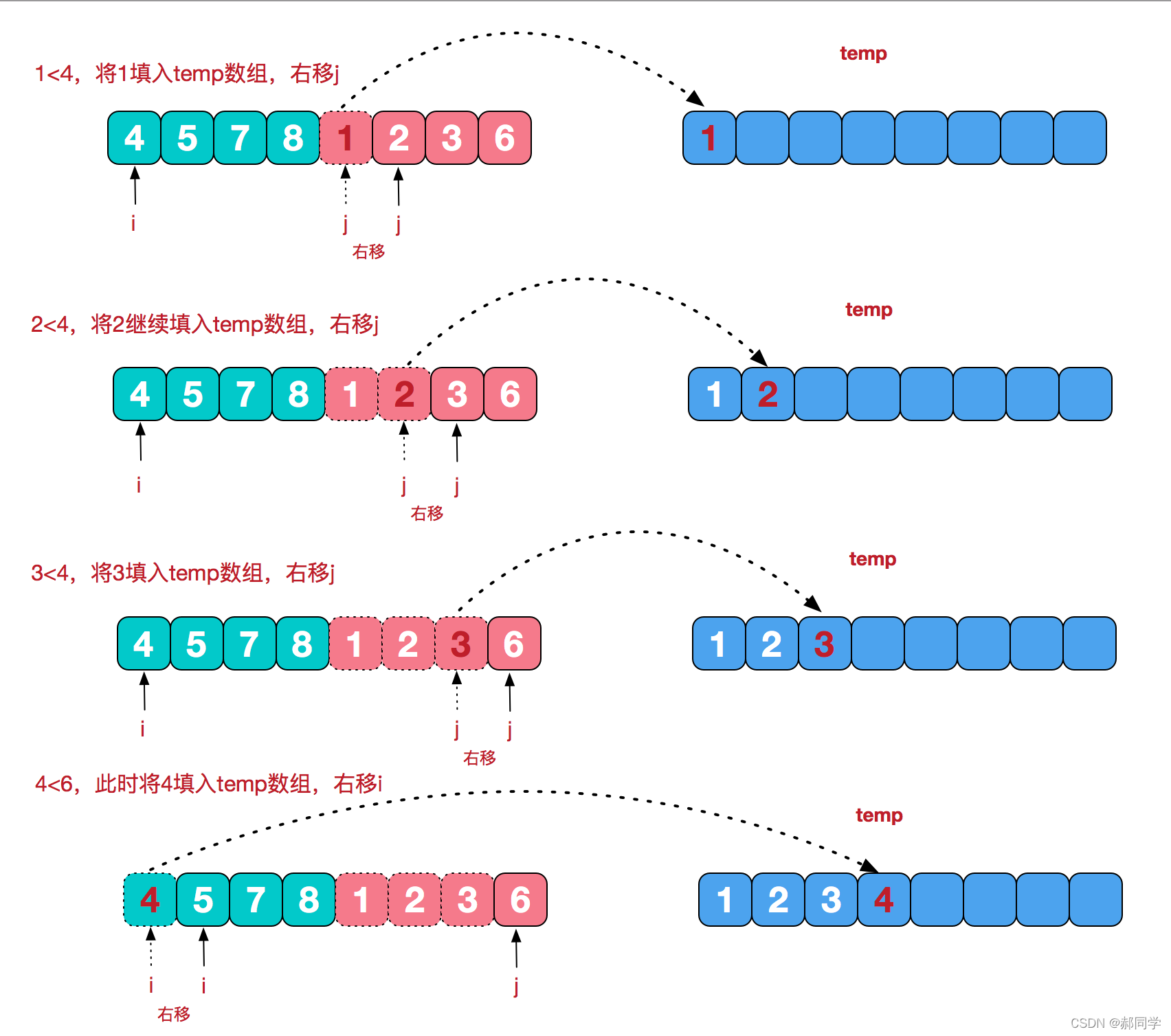
上图参考来自于：图解排序算法(四)之归并排序

0x01 利用归并排序来计算数组中逆序对个数：

class Solution {
   
   
public:
    // 利用归并排序的性质来判断中间过程的大小比较，从而计算其中的逆序对的个数
    // 归并排序的平均之间复杂度是O(nlogn)
    
    int revNum = 0;  // 保存逆序对的个数
    vector<int> tmp; // 定一个临时数组
    int reversePairs(vector<int>& nums) {
   
   
        int nLength = nums.size();
        tmp.resize(nLength);
        mergeSort(nums, 0, nLength-1);
        return revNum;
    }
    void mergeSort(vector<int> &nums, int left, int right) {
   
   
        if (left>=right) return;
        int mid = left+(right-left)/2;
        // 左拆分
        mergeSort(nums, left, mid);
        // 右拆分
        mergeSort(nums, mid+1, right);
        // 合并相邻两部分
        merge(nums