一篇文章带你搞懂二分

二分

到底什么是二分呢？二分二分就是一分为二。简单来说二分就是在有序序列中，通过不断的二分，进而不断地缩小范围去寻找满足我们条件的解。这只是对二分一个狭义上的理解，广义二分其实是如果有一个临界值使得临界值一边的数据满足一种性质，另一边满足另一种性质，即使不是有序的但也可以利用二分去寻找这个临界值。
在信息学竞赛中，二分题目主要分为二分查找、二分答案，二分类型分为整数二分、实数域上二分

整数二分

在写整数二分时，可以分为两种情况，一种将数轴分为[L,mid],[mid+1,R]两个部分，另一种将数轴分为[L,mid-1],[mid,R]两个部分，现在可能还不懂这是什么东西，我们接下来结合题目讲解。首先来看一下二分的基本模板吧

// 将区间分为[L,mid],[mid+1,R]
bool check(mid){//判断条件函数 
}
//终止条件是left==right 
while(left<right){
	int mid=(left+right)>>1;//这里使用右移运算主要是在负数时右移向下取整，除法向零取整
	if(check(mid)) right=mid;//判断如果mid这个值满足[L,mid]这个区间里面的的数的性质，则将r=mid，缩小范围 
	else left=mid+1; //否则另l=mid+1，+1的原因是mid不满足条件不能取 
}
cout<<left;



// 将区间分为[L,mid-1],[mid,R]
while(left<right){
	int mid=(left+right+1)>>1;//这里一定要加1！原因稍后再讲 
	if(check(mid)) left=mid;//判断如果mid这个值满足[mid,R]这个区间里面的的数的性质，则将l=mid，缩小范围 
	else right=mid-1; //否则另r=mid-1，+1的原因是mid不满足条件不能取 
}
cout<<left;

看到上面的代码我相信你现在一定是一脸懵逼，没事我们接下来结合具体问题讲解

请看下面一道题，请在序列1 4 7 9 10中寻找大于等于8的第一个数

在做整数二分题目时，刚开始学习的比较困难的是选择上面的哪一个模板，我们先来分析一下这道题，这道题要求寻找第一个大于等于8的数，及以这个数为分界点，右边的都满足这个性质，左边的都不满足，很显然当mid>=8时，我们应该在下一次二分时让mid左移动，去寻找第一个>=8的数，所以下一次的查找区间应该是在[L,mid]中，很显然符合第一个情况。接下来我们结合图片了解一下每一步，首先先贴上代码便于食用

#include<iostream>
using namespace std;
int a[5]={1,4,7,9,10};
int right_bound(int x){
	int l=0;int r=5;
	while(l<r){
		int mid=(l+r)>>1;//跟(l+r)/2不同的是右移向下取整，除运算向零取整 
		if(a[mid]>=x) r=mid;//求的是闭区间 
		else l=mid+1;
	}
	return a[r];
}
int main(){
	cout<<right_bound(8);
	
}

查找过程：
最初：

第一次查找：
计算出mid=（l+r）>>1=3（注意下标从0开始）, 发现9比8大，为了寻找比8大的第一个数，就需要向左缩小范围，因为mid是满足条件的，所以另r=mid


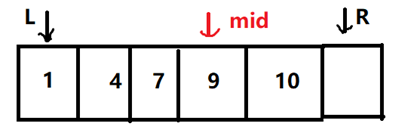
第二次查找：
计算出mid=（l+r）>>1=1，显然4是小于8的就不满足条件，就需要向右缩小范围，因为mid不满足我们的条件，我们的需求是找到大于等于8的第一个数，所以l=mid+1。


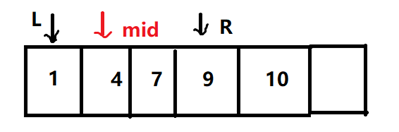
第三次查找：
计算出mid=（l+r）>>1=2，由if(a[mid]>=x) r=mid; else l=mid+1，移动左指针，即改变l的值l=9


因为L==R，结束循环，输出答案

通过刚才的模拟，我相信大家对二分查找的过程肯定有大致的了解，但是在真实的做题中，往往困难的地方是对二分模板的选择方面，这个是值得大家思考的地方。

如果把题目改成小于等于8的第一个数呢？

显然这就要用到第二个模板了，过程就交给你们模拟了，直接贴代码

#include<iostream>
using namespace std;
int a[5]={1,4,7,9,10};
int left_bound(int x){
	int l=0;int r=5;
	while(l<r){
		int mid=(l+r+1)>>1;//注意这里要+1 
		if(a[mid]<=x) l=mid;//求的是闭区间 
		else r=mid-1;
	}
	return a[r];
}
int main(){
	cout<<left_bound(8);
	
}

注意这里 mid=(l+r+1)>>1+1的主要原因是如果r-l=1，因为>>1是向下取整，所以mid=l，如果很不幸if(check()) l=mid;成立的话，你就会陷入无尽的死循环中。

总结：该模板保证最终答案处于闭区间[l,r]以内，循环以l=r结束，每次二分的中间值mid会归属于左半段与右半段二者之一，优点是几乎可以用于所有的二分题型，但缺点是需要分清楚两种情况，并根据实际情况选择相应的模板。

实数域上二分

相比较整数上的二分，实数域上的二分就简单很多了，实数域上二分需要注意的点是确定精度，这里有一个小技巧，如果题目上让保留k位小数，那么精度eps
就设置成1e^(-k-2)

//具体情况具体分析
double l=0,r=1000;//这里l与r的值一定要根据题目来设定，不能想当然的就从0开始
while(r-l>eps){
	double mid=(r-l)/2;
	if(check()) l=mid;
	else r=mid;
} 
cout<<l;

有的时候精度难以控制，也可以用设立二分次数的方法来控制精度

//具体情况具体分析
#include<iostream>
using namespace std;
int main(){
	double l=0,r=1000;
	for(int i=0;i<100;i++){
		double mid=(l+r)/2;
		if(check()) l=mid;
		else r=mid;
	}
	
	printf("%lf",l);
}

二分查找

二分查找也称折半查找，可以提高查找效率，上面的例题就是二分查找的一个实例，所以这里就不再赘述。重点在二分答案

二分答案

二分答案全称叫做二分答案转化为判定，这类问题通常用于答案的值域已经确定，并且很难从问题的本身去找到答案，这样就可以从答案值域入手，判定这个值符不符合题目要求，根据判定结果缩小范围从而找到最优值。

例题 ： 数列分段

这道题我能想到的暴力做法是把所有的情况找出来，然后比较每段和的最大值从而找到每段和的最大值的最小值。这个思路想一想实现起来就比较麻烦，所以通过观察发现最大值的范围其实是固定的，它最大也不会超过整个序列的和，最小也不会小于这个序列中最大的那个数。那么我们就可以通过二分在这个范围进行查找，直到找到那个满足要求并且最小的那一个。
现在大致思路明白了，就要选择用哪一个模板，因为题目要求求最小值，也就是求刚好满足条件>=x的那个数，x为最小的和，很显然用的是[l,mid],[mid+1,r]这个区间的模板。如果mid导致分得的组数小于等于M了，就另r=mid，进一步缩小范围，因为mid越小分得的组数越多，否则另l=mid+1。

#include<iostream>
using namespace std;
const int N=1e5+10;
int n,m,a[N];
bool check(int x){//判断如果选择x作为每组的最大厚度，形成的组数，如果小于等于m就需要另最大厚度变小 ，反之变大 
	int t=1,size=x;
	for(int i=1;i<=n;i++){
		if(a[i]<=size) size=size-a[i];
		else size=x-a[i],t++;
	}
	return t<=m;
}
int main(){
	cin>>n>>m;
	int sum=0;
	int l=0,r;
	for(int i=1;i<=n;i++){
		cin>>a[i];
		l=max(l,a[i]);
		sum+=a[i];
	}
	r=sum;
	while(l<r){
		int mid=(l+r)>>1;
		if(check(mid)) r=mid;
		else l=mid+1;
	}
	cout<<l;
	
	
}

从上面那道题中不难看出把查找转化为了判定可以大大提高了我们的效率也简化了问题，做这类题目主要是要写好check（）函数，确定好值域范围