斐波那契数列(Fibonacci Sequence)多种解法与矩阵快速幂详解

---

问题背景

求斐波那契数列 (Fibonacci Sequence)的第N项，波那契数列的定义如下：

• F(0)=0
• F(1)=1
• F(N)=F(N−1)+F(N−2) for N≥2

每一个数是前两个数的和。例如：0,1,1,2,3,5,8,13,21,34,55…
本文讲解斐波那契数列的几种常见解法，包括各方法的优缺点和具体python实现。

---

1. 递归方法

递归方法是最直观的实现方式，直接根据斐波那契数列的定义进行计算。

优点

实现简单直观。

缺点

存在大量重复计算，效率低下。
时间复杂度高，为O(n^2)。

实现代码

def fib_recursive(n):
    if n <= 1:
        return n 
    return fib_recursive(n-1) + fib_recursive(n-2)

2. 带备忘录的递归方法（记忆化递归）

通过记忆化递归（Memoization），可以避免重复计算，从而提高效率。

优点

时间复杂度降为 O(n)同时保留了递归的简洁写法。

缺点

使用额外的空间来存储已经计算的结果，空间复杂度为 O(n)。
实现代码

def fib_memo(n, memo=None):
    if memo is None:
        memo = {}
    if n in memo:
        return memo[n]
    if n <= 1:
        return n
    memo[n] = fib_memo(n-1, memo) + fib_memo(n-2, memo)
    return memo[n]

3. 动态规划

动态规划方法通常采用迭代的方式，从已知的斐波那契数开始，逐步计算直到目标数。这种方法避免了递归中的重复计算，同时也避免了递归的深度过深导致的栈溢出问题。

优点

时间复杂度为O(n)，效率高。
不需要额外的空间来存储中间结果，空间复杂度为O(1)。

缺点

实现相对复杂，需要理解动态规划的思想。

实现代码

def fib_dp(n):
    if n <= 1:
        return n
    dp = [0] * (n + 1)
    dp[1] = 1
    for i in range(2, n + 1):
        dp[i] = dp[i-1] + dp[i-2]
    return dp[n]

4. 优化的动态规划

在动态规划中，我们可以进一步优化空间复杂度，只需存储最近的两个数值即可，不需要存储整个数组。

优点

空间复杂度进一步优化到O(1)。

缺点

可读性略差，需要理解算法的思想。

实现代码

def fib_optimized(n):
    if n <= 1:
        return n
    a, b = 0, 1
    for _ in range(2, n + 1):
        a, b = b, a + b
    return b

5. 矩阵快速幂

矩阵快速幂是一种高效的计算斐波那契数列的方法，尤其适用于需要计算大量斐波那契数的情况。

优点

时间复杂度为 O(logn)，效率高。
可以处理非常大的n。

缺点

实现相对复杂，需要理解矩阵快速幂的原理。

实现代码

def matrix_mult(A, B):
    return [
        [A[0][0] * B[0][0] + A[0][1] * B[1][0], A[0][0] * B[0][1] + A[0][1] * B[1][1]],
        [A[1][0] * B[0][0] + A[1][1] * B[1][0], A[1][0] * B[0][1] + A[1][1] * B[1][1]]
    ]

def matrix_pow(A, n):
    result = [[1, 0], [0, 1]]  # 单位矩阵
    while n > 0:
        if n % 2 == 1:
            result = matrix_mult(result, A)
        A = matrix_mult(A, A)
        n //= 2
    return result

def fib_matrix(n):
    if n <= 1:
        return n
    F = [[1, 1], [1, 0]]
    result = matrix_pow(F, n-1)
    return result[0][0]

矩阵乘法

矩阵可以看作是一种能够很好地描述线性递推关系的特殊表格，它能帮助我们用一种新的方式看待斐波那契数。我们不需要深刻理解矩阵，只需要知道它是如何帮助我们计算的。

我们首先构造一个特别的矩阵A如下：

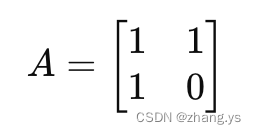
为什么要这样构造呢？
因为这个矩阵有个神奇的性质：如果我们将这个矩阵与一个包含两个连续斐波那契数的向量相乘，我们会得到下一个斐波那契数。例如：

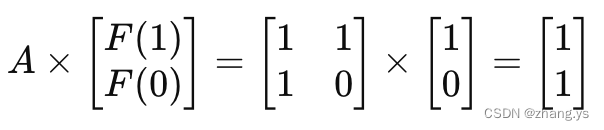
即F(0)和F(1)组成的向量与A相乘后，新的向量包含了下一个斐波那契数F(2)和它的前一个数F(1)

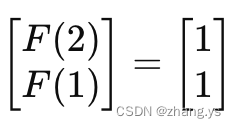
有了这个特性，我们就可以重复这个过程，通过多次相乘矩阵A，得到更高的斐波那契数。例如：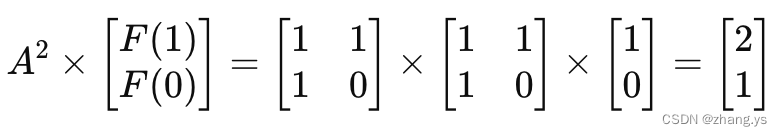
这个计算结果即F(3)=2和F(2)=1。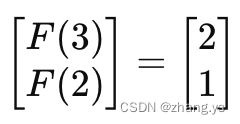
有了这个思路，我们就可以计算出F(n)的结果。

快速幂

但是问题来了，这种方式与动态规划相比并没有什么优势，如果我们想计算一个很大的 n 的斐波那契数，比如F(1000)，直接反复相乘会非常慢。这里就需要用到一种叫“快速幂”的方法来优化时间复杂度。

快速幂的核心思想是利用指数的二进制表示来减少乘法次数。举个简单的例子，计算A^8可以表示成(A^4)^2，而A^4可以表示成(A^2)^2，所以我们只需要计算两次平方((A^2)^2)^2，而不是八次乘法。

通过这种方法，我们能够在较短的时间内计算出非常大的斐波那契数。希望本文能帮助大家理解矩阵快速幂计算斐波那契数的原理，如果还有疑问，请在评论区留言。