【复习笔记】二叉排序树、平衡二叉树、哈夫曼树

bugcoder-9905

已于 2022-04-17 20:38:58 修改

阅读量1.6k

点赞数 1

分类专栏：数据结构文章标签：算法数据结构

于 2020-08-03 17:44:41 首次发布

本文链接：https://blog.csdn.net/qq_42500831/article/details/107758431

版权

数据结构专栏收录该内容

38 篇文章 7 订阅

订阅专栏

文章目录

一、二叉排序树（Binary Search Tree）

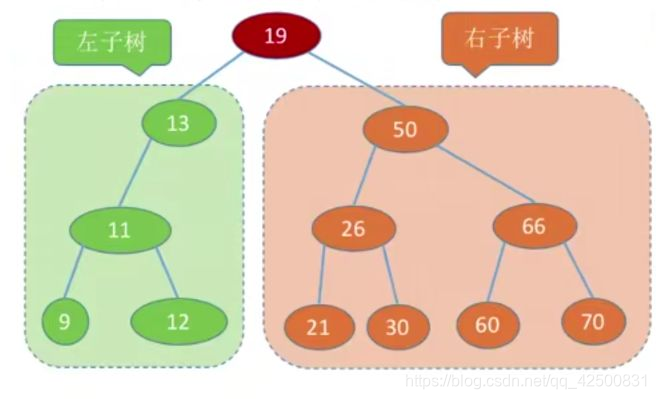
定义： 二叉排序树又称二叉查找树，对于任何一个结点满足条件：左子树结点值<根节点值<右子树结点值。二叉排序树中序遍历结果是一个升序序列。

以下便是一棵二叉排序树：
在这里插入图片描述

二叉树结点定义

struct TreeNode {
    int val;
    TreeNode *left;
    TreeNode *right;
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

1. 插入结点

无论是否插入成功，都返回原来树的跟结点。并用布尔值isInserted返回是否插入成功。

非递归插入（BFS）


TreeNode* insertIntoBST(TreeNode* root, int val, bool* isInserted) {
    if (root == nullptr) return new TreeNode(val);
    TreeNode* head = root;
    while (root) {
    	//插入的值太小，往左边深入
        if (val < root->val) {
            if (root->left == nullptr) {
                root->left = new TreeNode(val);
                *isInserted= true;
                return head;     //成功插入结点
            }
            else root = root->left;
        }
        //插入的值太大，往右边深入
        else {
            if (root->right == nullptr) {
                root->right = new TreeNode(val);
                *isInserted= true;
                return head;    //成功插入结点
            }
            else root = root->right;
        }
    }
    return head;  //没插入结点
}

/*
	调用方式：
	bool isInserted = false;
	insertIntoBST(root, val, &isInserted);
*/

递归插入（DFS）

TreeNode* insertIntoBST(TreeNode* root, int val, bool* isInserted) {
    if (root == nullptr) {
        *isInserted= true;
        return new TreeNode(val);  //当前深入的结点为空，生成（new）新结点，挂上（return）
    }else if (val < root->val) {
        root->left = insertIntoBST(root->left, val, isInserted); //插入值比当前结点小，往左边深入
    }else if(val > root->val){
        root->right = insertIntoBST(root->right, val, isInserted);//插入值比当前结点大，往右边深入
    } 
    return root;  // 传入的哪个结点，就在哪个结点挂上，再返回
}

/*
	调用方式：
	bool isInserted= false;
	insertIntoBST(root, val, &isInserted);
*/

2. 构造二叉排序树

所谓构造，就是按照顺序一个一个插入。

TreeNode* insertIntoBST(TreeNode* root, int val) {
    if (root == nullptr) {
        TreeNode* root = new TreeNode(val);
        return root;
    }else if (val < root->val) {
        root->left = insertIntoBST(root->left, val);
    }else if(val > root->val){
        root->right = insertIntoBST(root->right, val);
    } 
    return root;
}

TreeNode* Create_BST(vector<int> nums){
    TreeNode* root = nullptr;   //初始时，树为空
    for(int num : nums){
        root = insertIntoBST(root, num);
    }
    return root;
}

注：对于元素相同但顺序不同的数组，构造的二叉排序树也可能不同

3. 查找结点

找到则值为key的结点，找不到则返回nullptr

非递归查找：

TreeNode* BST_Search(TreeNode* node, int key){
    while(node != nullptr && node->val != key){
        if(node->val < key){
            node = node->right;      //查找的值过大，在右节点查找
        }else{
            node = node->left;       //查找的值过小，在左节点查找
        }
    }
    return node;                     //找到了key，或不存在值为key的结点
}

注：由于每次只会访问一个结点，最坏时间复杂度为O(1)

递归查找：

TreeNode* BST_Search(TreeNode* node, int key){
    if(node == nullptr){
        return nullptr;
    }
    if(node->val == key){
        return node;
    }else if(node->val < key){
        BST_Search(node->right, key);
    }else{
        BST_Search(node->left, key);
    }
}

注：空间复杂度和二叉树的深度有关，每层的递归都会在函数调用栈里多分配一片空间，所以最坏时间复杂度为O(h)

4. 删除结点

若被删除结点node为叶节点，直接删除即可
若被删除结点node只有一棵子树，则让node的子树成为node父结点的子树即可
若被删除结点node有两颗子树，如下：

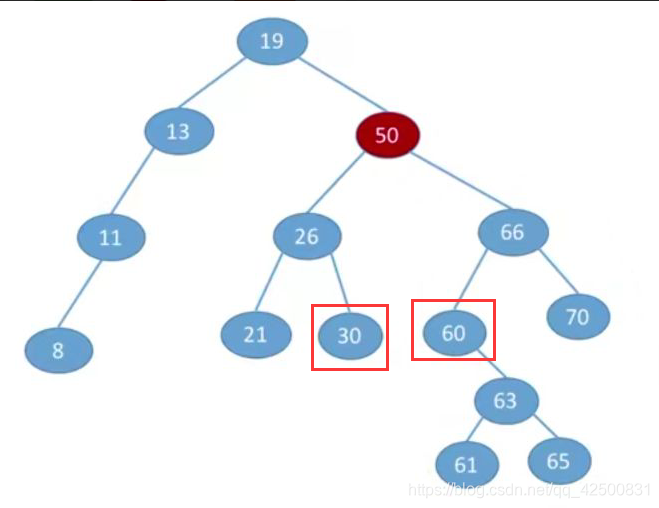
这时需要在右子树中找到一个最小的结点（30），或在左子树中找到一个最大的结点（60），将该结点的值赋给被删除结点的值。然后再删除我们找到的这个结点即可（这时的删除操作就转换成前两种删除操作了）。

二、平衡二叉树（AVL树）

满足条件： 树上任一结点左子树和右子树高度之差不大于1
结点平衡因子： 左子树高 - 右子树高，取值范围为[-1,1]
最小不平衡子树： 从插入点往回找到第一个不平衡结点，以该结点为根的子树

在一棵BST树上插入新结点之后如何保持平衡性？
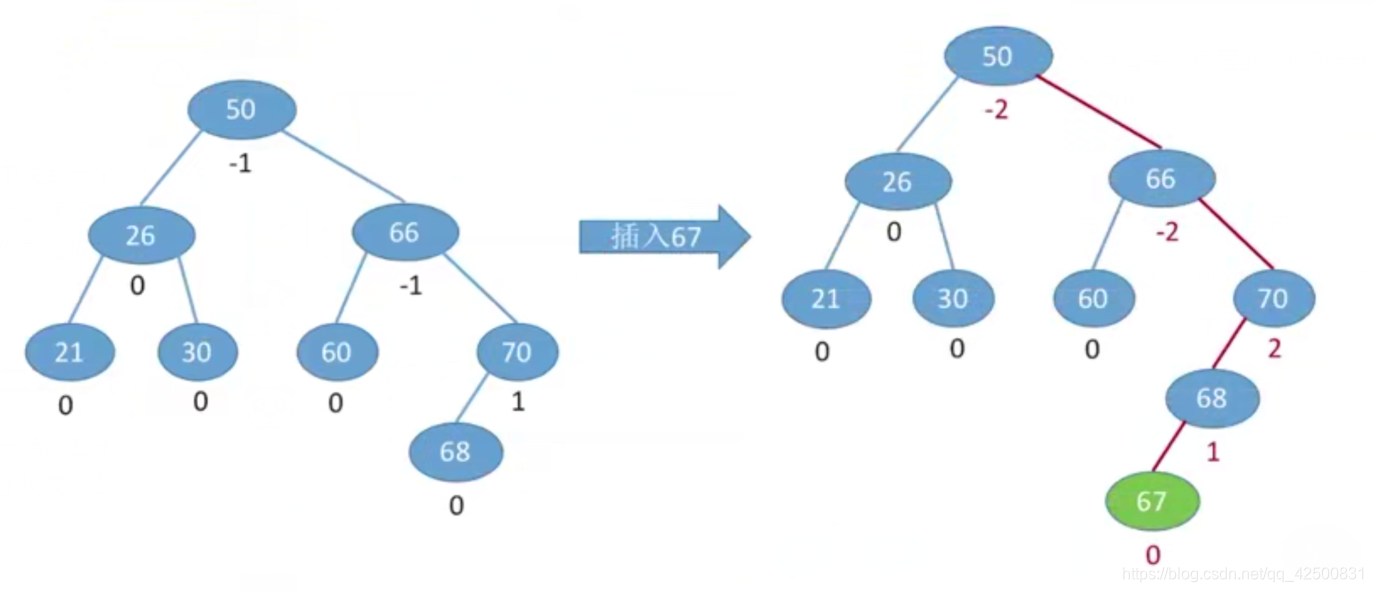
在这里插入图片描述
我们只需要调整最小不平衡子树即可。因为当插入新结点后，若破坏了二叉树的平衡性，则整个二叉树高度必加1。只要恢复从插入点往回找到第一个不平衡结点的高度，则上面所有结点的平衡因子全部恢复。

调整结果如下：
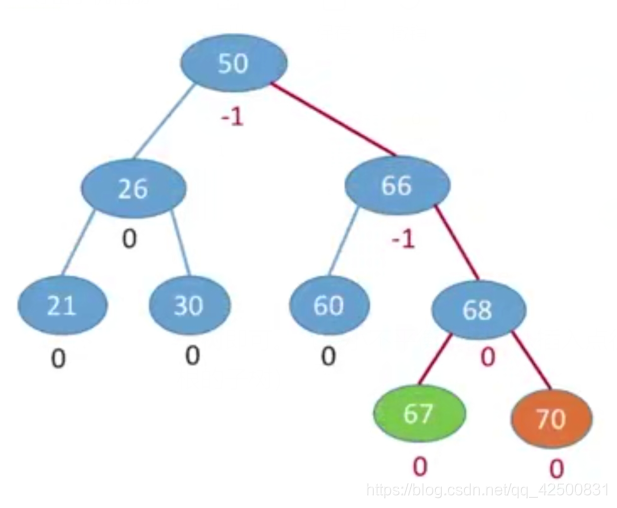
在这里插入图片描述

调整最小不平衡子树A

1. 在A的左孩子的左子树中插入导致不平衡（LL）

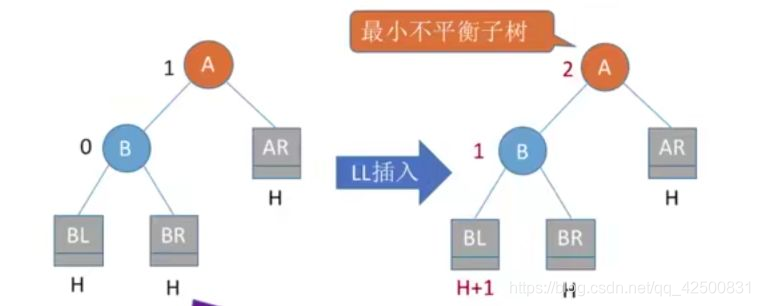
在这里插入图片描述
可以看到，结点A的平衡因子变成了2，此时最小不平衡子树就是以A为根节点的二叉树。此时对于这棵最小不平衡子树上结点的值有：BL<B<BR<A<AR

恢复平衡的方法： 右旋，调整根结点的左孩子。将A的左孩子 B向右上旋转代替A成为根结点，将A结点向右下旋转成为B的右子树的根节点，而B的原右子树（BR）则成为A结点的左子树，其他结点不变。

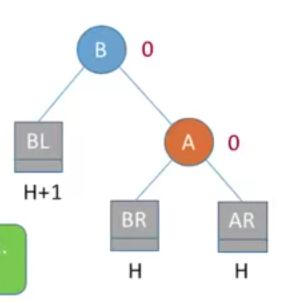
在这里插入图片描述

2. 在A的右孩子的右子树中插入导致不平衡（RR）

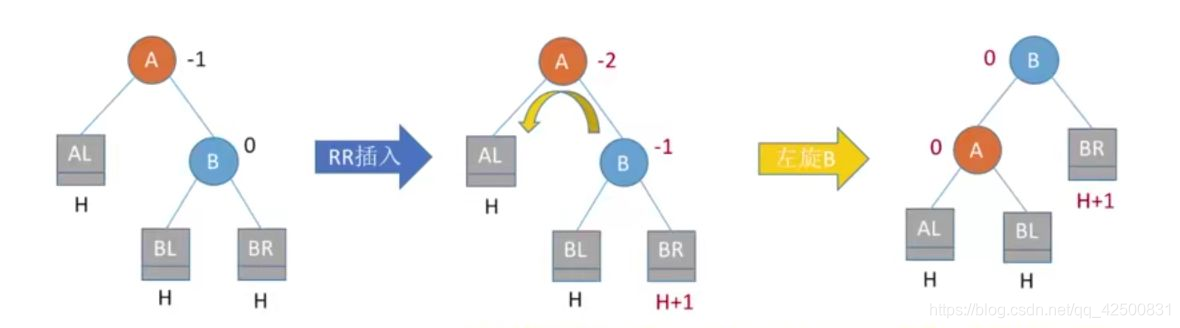
在这里插入图片描述
结点值的大小关系：AL<A<BL<B<BR

从中间的图可以看到，我们需要进行一次左旋操作，调整根结点的右孩子。将A的右孩子B向左上旋转代替A成为根结点，将A结点向左下旋转成为B的左子树的根结点，而B的原左子树（BL）则成为A的右子树，其他不变。

3. 在A的左孩子的右子树中插入导致不平衡（LR）

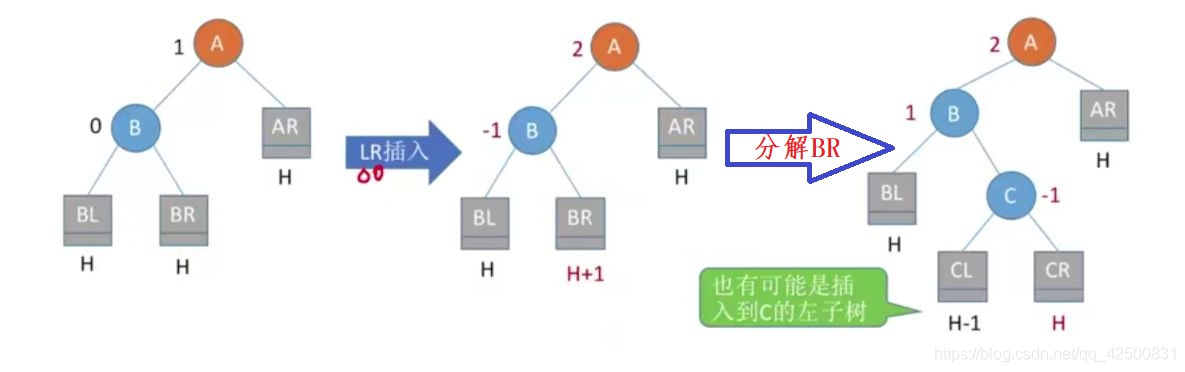
在这里插入图片描述
由于在A的左孩子（L）的右子树（R）上插入新结点，A的平衡因子由1增加为2，导致以A为根的子树失去平衡，需要进行两次旋转，先左后右，调整结点C（根结点的左孩子的右孩子）。

处理方法：将C向左上旋转提升到B结点的位置，B成为C的左结点，把C结点向右上旋转提升到A结点的位置，A成为C的右结点。其他结点按照大小顺序：BL<B<CL<C<CR<A<AR 挂上即可。
加粗样式

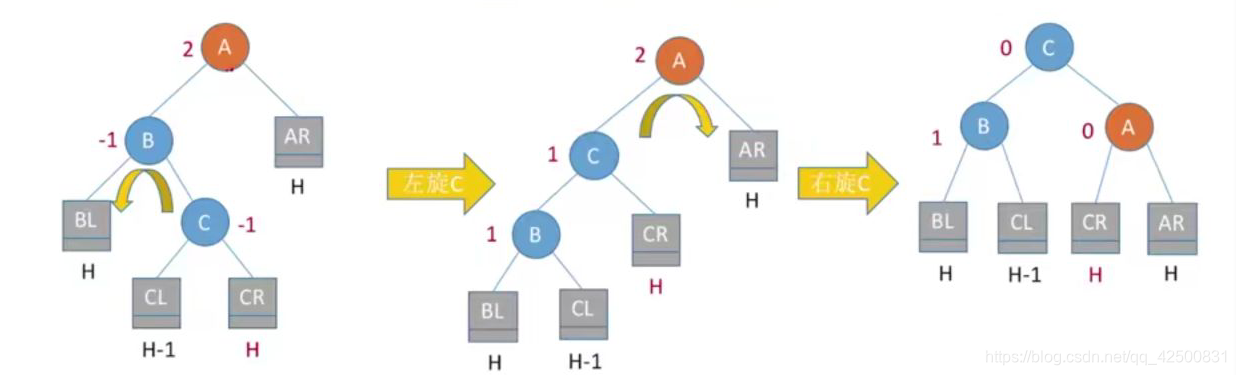
4. 在A的右孩子的左子树中插入导致不平衡（RL）

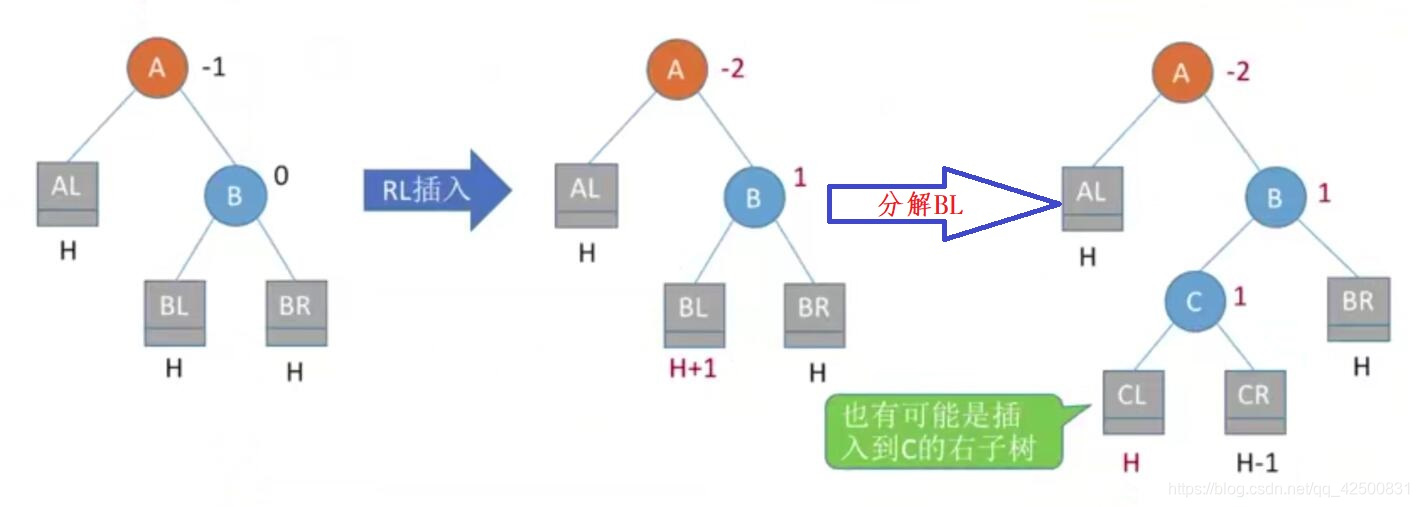
在这里插入图片描述

处理方法：两次旋转，先右后左，调整结点C（根结点的右孩子的左孩子） 将C向右上旋转提升到B结点的位置**，B成为C的右结点，把C结点向左上旋转提升到A结点的位置，A成为C的左结点。其他结点按照大小顺序：AL<A<CL<C<CR<B<BR 挂上即可。

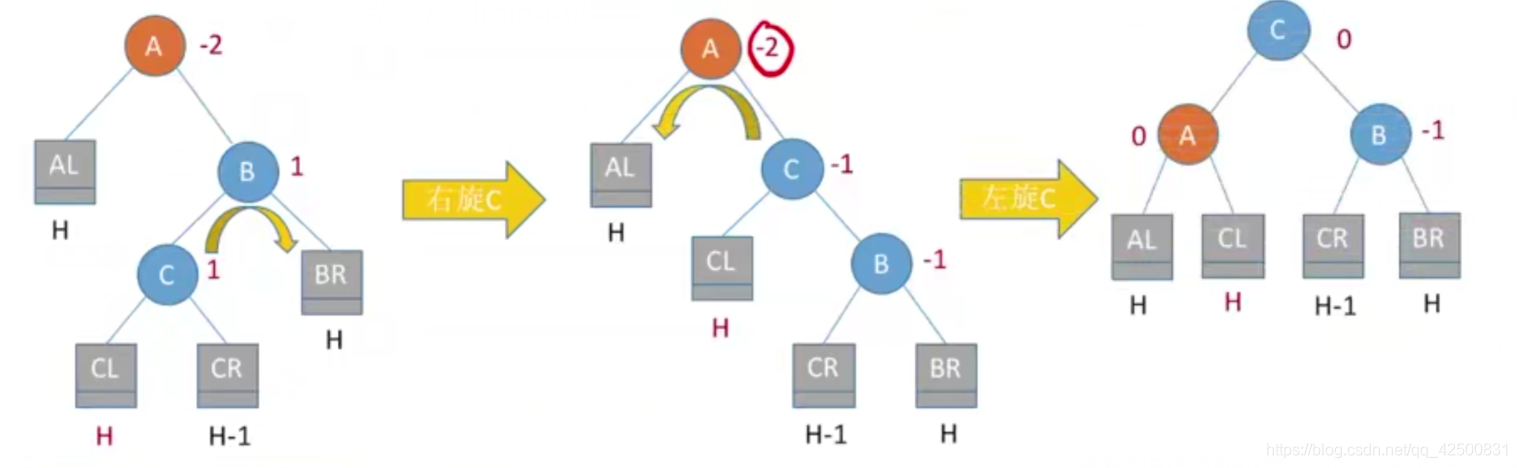
在这里插入图片描述

旋转操作总结：
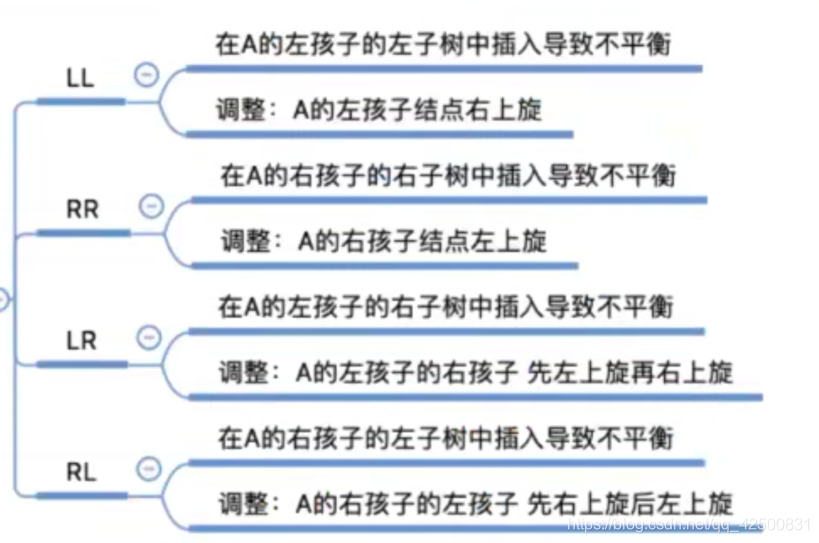
在这里插入图片描述

用 $N_h$ 表示深度为 $h$ 的平衡二叉树含有的最少结点数，则有：
$N_0=0，N_1=1，N_2=2$ ，且 $N_h = N_{h-1}+N_{h-2}+1$

判断平衡二叉树

在这里插入图片描述
方法一：暴力法

构造一个获取当前节点最大深度的方法 $g e t D e p t h (r o o t)$ ，通过比较此子树的左右子树的最大高度差，来判断此子树是否是二叉平衡树。若树的所有子树都平衡时，此树才平衡。

class Solution {
public:
    int getDepth(TreeNode* root){
        if(root == nullptr){
            return 0;
        }
        return max(getDepth(root->left), getDepth(root->right)) + 1;
    }

    bool isBalanced(TreeNode* root) {
    	// 当前结点为空，直接返回true
        if(root == nullptr){
            return true;
        }
		// 先序遍历递归
		// 当前二叉树是否平衡 && 左子树是否平衡 && 右子树是否平衡
        return abs(getDepth(root->left) - getDepth(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);
    }
};

复杂度分析：

时间复杂度 $O(Nlog_2 N)O(Nlog 2N)$ ：最差情况下， $i s B a l a n c e d (r o o t)$ 遍历树所有节点，占用 $O (N)$ ；判断每个节点的最大高度 $d e p t h (r o o t)$ 需要遍历各子树的所有节点，子树的节点数的复杂度为 $O(log_2 N)O(log2N)$
空间复杂度 $O (N)$ ：最差情况下（树退化为链表时），系统递归需要使用 $O (N)$ 的栈空间。

方法二：自底向上、提前阻断

算法流程：
$r e c u r (r o o t)$

递归返回值：

当节点root 左 / 右子树的高度差<2 ：则返回以节点root为根节点的子树的 最大高度
当节点root 左 / 右子树的高度差≥2 ：则返回-1 ，代表 此子树不是平衡树

递归终止条件：

当越过叶子节点时，返回高度 0
当左（右）子树高度 left = -1 时，代表此子树的左（右）子树不是平衡树，因此直接返回 -1

复杂度分析

时间复杂度 $O (N)$ ： $N$ 为树的节点数；最差情况下，需要递归遍历树的所有节点。
空间复杂度 $O (N)$ ：最差情况下（树退化为链表时），系统递归需要使用 $O (N)$ 的栈空间

class Solution {
public:
    int recur(TreeNode* root){
        if(root == nullptr)  return 0;
        int lh = recur(root->left);
        if(lh == -1)  return -1;
        int rh = recur(root->right);
        if(rh == -1)  return -1;
        // 当前子树若平衡，则返回子树高度。否则返回-1，代表不平衡
        return abs(lh - rh) <= 1 ? max(lh, rh) + 1 : -1;
    }

    bool isBalanced(TreeNode* root) {
        return recur(root) != -1;
    }
};

参考题解

三、哈夫曼树

1. 一些基本概念

结点的权： 有某种现实含义的数值
结点的带权路径长度： 从结点的根到该结点的路径长度与该结点权值的乘积
树的带权路径长度： 树上所有叶结点的带权路径长度之和（ $wpl=\sum\limits_{i=1}^{n}w_il_i$ ）
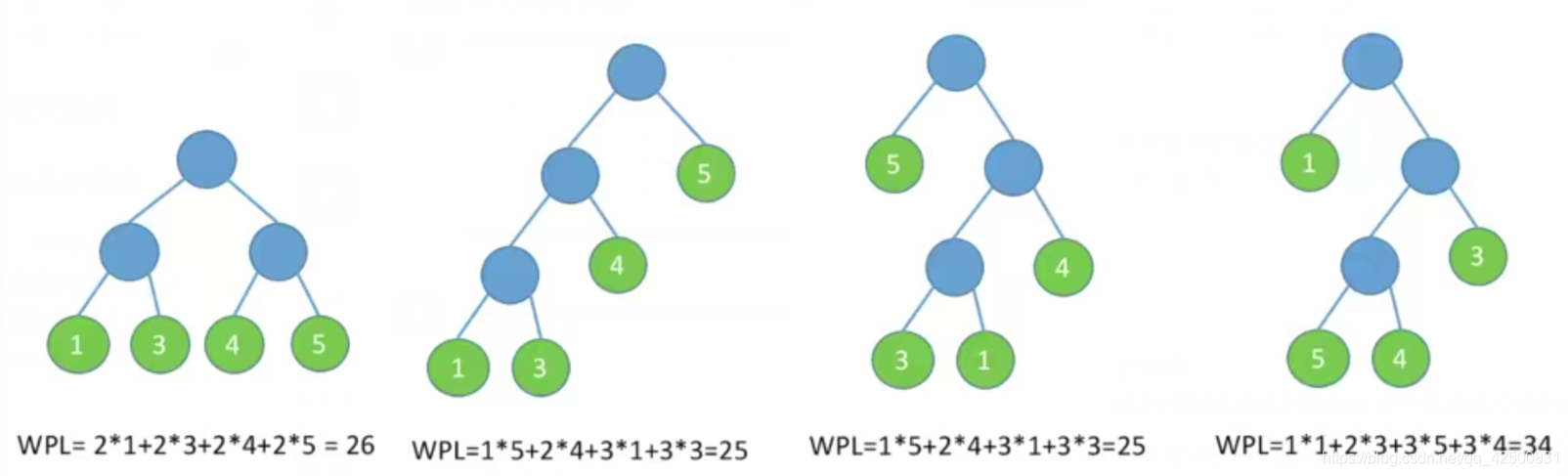
在这里插入图片描述
哈夫曼树： 在含有 $n$ 个带权叶结点的二叉树中， $w p l$ 最小的二叉树称为哈夫曼树，也称最优二叉树（给定叶子结点，哈夫曼树不唯一）。

2. 构造哈夫曼树

比较简单，此处不赘述步骤
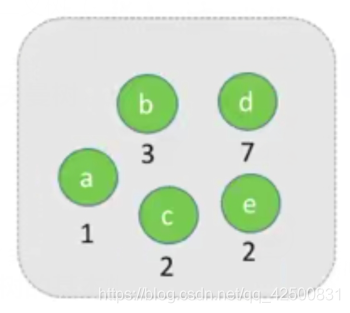
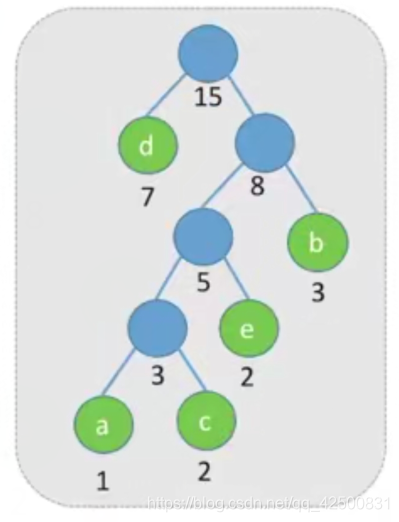
在这里插入图片描述

在这里插入图片描述

3. 哈夫曼树的基本性质

每个初始结点最终都是叶结点，且权值越小的结点到根结点的路径长度越大
具有 $n$ 个根结点的哈夫曼树的结点总数为 $2 n - 1$
哈夫曼树中不存在度为1的结点
哈夫曼树不唯一，但 $w p l$ 必然相同且最优

4. 哈夫曼编码

在考试中，小渣利用哈夫曼编码老渣发电报传递100道选择题的答案，小渣传递了10个A、8个B、80个C、2个D，老渣利用哈夫曼编码的方式解码。

小渣构造的哈夫曼树如下：
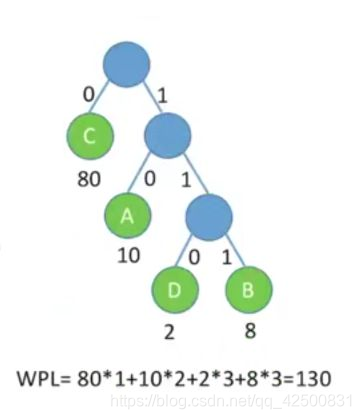
在这里插入图片描述
可以发现，A、B、C、D的编码分别为10、111、0、110。

这样小渣只要根据1~100题的答案顺序发送01序列，老渣收到后进行解码就能正确收到答案了。而且哈夫曼编码的方式不会有歧义，因为哈夫曼编码是一种前缀编码。

前缀编码： 没有一个编码是另一个编码的前缀，因为数据节点都是叶子节点。如果出现一个字符的编码是另一个字符编码的前缀，那这个字符一定处于内部节点，这是不可能的
由哈夫曼树得到的哈夫曼编码： 字符集中的每个字符都是以叶子结点出现在哈夫曼树中，各个字符出现的频率为结点的权值。

给字符串进行编码的时候，由于出现频率越高（权值大）的字符距离根节点越进，编码越短；只有出现频率越低（权值小）的字符距离根节点较远，编码长。没关系，由于频率高的字符编码都短，所以哈夫曼编码可以得到最短的编码序列

bugcoder-9905

关注

1
点赞
踩
6

收藏

觉得还不错? 一键收藏
打赏
1
评论
【复习笔记】二叉排序树、平衡二叉树、哈夫曼树

一、二叉排序树（Binary Search Tree）定义：二叉排序树又称二叉查找树，对于任何一个结点满足条件：左子树结点值<根节点值<右子树结点值。二叉排序树中序遍历结果是一个升序序列。以下便是一棵二叉排序树：二叉树结点定义struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode(int x) : val(x), left(NULL), right(NULL) {}};
复制链接

扫一扫