回文子串（DP）

回文子串

1. 动态规划法

首先这一题可以使用动态规划来进行解决：

• 状态：$dp[i][j]$ 表示字符串s在$[i,j$]区间的子串是否是一个回文串

• 状态转移方程：当 $s[i]==s[j]\&\&(j-i<2||dp[i+1][j-1])$ 时，$dp[i][j]=true$，否则为false

这个状态转移方程是什么意思呢？

• 当只有1个字符时，比如 a 自然是一个回文串
• 当有2~3个字符时，如果首尾字符是相等的，比如 aa或ana，也是一个回文串
• 当有三个及以上字符时，比如 ababa 这个字符记作串 1，把首尾的 a 去掉，也就是 bab 记作串 2，可以看出只要串2是一个回文串，那么左右各多了一个 a 的串 1 必定也是回文串。所以当$s[i]==s[j]$ 时，自然要看 $dp[i+1][j-1]$ 是不是一个回文串

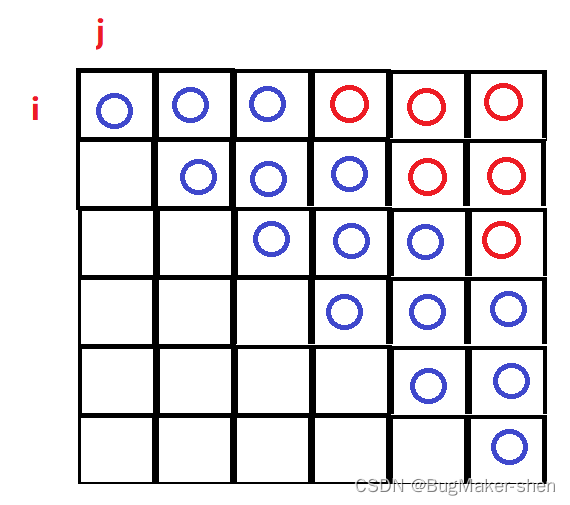
填写6x6 dp数组的顺序如下

当字串长度不超过3（j-i <= 2），如果首尾字符相等，就能确定当前字串是回文串，即图中蓝色方格填写不需要查询dp数组

而红色方格处需要查询dp数组，查询dp数组时需要查看当前方格左下角的值（左下角的数据记录了内侧子串是否是回文串），可以看到当填写红色方格时，左下角的已经填写了，可以用于查询

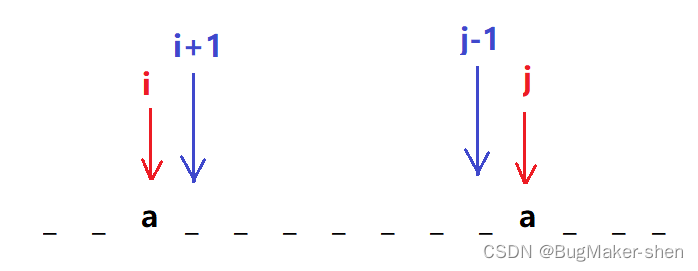
当我们判断字符串区间[i,j]内的子串是否是回文串时，如果两侧字符相等，我们需要判断内侧的子串是否是回文串（前面求解过，从dp数组直接查询），这样我们就能判断当前子串是否是回文串

class Solution {
public:
    int countSubstrings(string s) {
        int n = s.size();
        int cnt = 0;
        vector<vector<bool>> dp(n, vector<bool>(n, false));
        
        for(int j = 0; j < n; j++){
            for(int i = 0; i <= j; i++){
                if((s[i] == s[j]) && (j - i <= 2 || dp[i+1][j-1])){
                    dp[i][j] = true;
                    cnt++;
                }
            }
        }
        return cnt;
    }
};

class Solution {
public:
    int countSubstrings(string s) {
        int n = s.size();
        vector<vector<bool>> dp(n, vector<bool>(n, false));

        int cnt = 0;
        for(int gap = 0; gap < n; gap++){
            for(int i = 0; i < n - gap; i++){
                if(s[i] == s[i + gap]){
                    if(gap <= 2 || dp[i+1][i + gap - 1]){
                        dp[i][i + gap] = true;
                        cnt++;
                    }
                }
            }
        }
        return cnt;
    }
};

2. 中心拓展

中心拓展，就是挨个遍历，中心可能是1个字符也可能是2个字符

class Solution {
public:
    int cnt = 0;
	// 以一个字符为中心，回文串的长度为奇数
    void fun1(const string& s, int mid){
        cnt++;
        int l = mid - 1;
        int r = mid + 1;
        while(l >= 0 && r < s.size() && s[l] == s[r]){
        	// 不越界和两侧字符相等的情况下，数量++
            cnt++;
            l--;
            r++;
        }
    }
	// 以两个字符为中心，回文串的长度为偶数
    void fun2(const string& s, int l, int r){
        while(l >= 0 && r < s.size() && s[l] == s[r]){
            cnt++;
            l--;
            r++;
        }
    }

    int countSubstrings(string s) {        
        for(int i = 0; i < s.size(); i++){
            fun1(s, i);
            fun2(s, i, i+1);
        }
        return cnt;
    }
};

最长回文子串

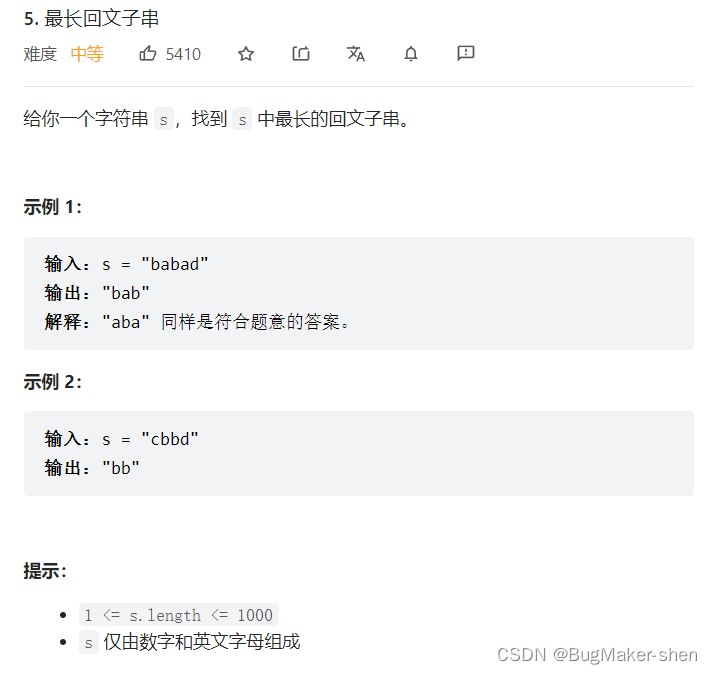
1. 动态规划

思路参考上一题

class Solution {
public:
    string longestPalindrome(string s) {
        int n = s.size();
        vector<vector<bool>> dp(n, vector<bool>(n, false));
        int l = 0;
        int r = 0;

        for(int j = 0; j < n; j++){
            for(int i = 0; i <= j; i++){
                if(s[i] == s[j] && (j - i <= 2 || dp[i+1][j-1])){
                    dp[i][j] = true;
                    if(j - i > r - l){
                        l = i;
                        r = j;
                    }
                }
            }
        }
        return string(s, l, r - l + 1);
    }
};

2. 中心扩展

思路参考上一题

class Solution {
public:
    int start = 0;
    int end = 0;
	// 以一个字符为中心，回文串的长度为奇数
    void fun1(const string& s, int mid){
        int l = mid - 1;
        int r = mid + 1;
        while(l >= 0 && r < s.size() && s[l] == s[r]){
        	// 不越界和两侧字符相等的情况下，数量++
            if(r - l > end - start){
                start = l;
                end = r;
            }
            l--;
            r++;
        }
    }
	// 以两个字符为中心，回文串的长度为偶数
    void fun2(const string& s, int l, int r){
        while(l >= 0 && r < s.size() && s[l] == s[r]){
            if(r - l > end - start){
                start = l;
                end = r;
            }
            l--;
            r++;
        }
    }

    string longestPalindrome(string s) {        
        for(int i = 0; i < s.size(); i++){
            fun1(s, i);
            fun2(s, i, i+1);
        }
        return string(s, start, end - start + 1);
    }
};

最长回文子序列

填写二维dp数组即可

dp[i][j]：i~j包含的最长回文子序列的长度

class Solution {
public:
    int longestPalindromeSubseq(string s) {
        int n = s.size();
        vector<vector<int>> dp(n, vector<int>(n, 0));
        
        for(int i = 0; i < n; i++) dp[i][i] = 1;
        for(int gap = 1; gap < n; gap++){
            for(int i = 0; i < n - gap; i++){
                if(s[i] == s[i + gap]){      // 首尾字符相同，内侧最长子序列（左下角） + 2
                    dp[i][i + gap] = dp[i + 1][i + gap - 1] + 2;
                }else{                       // 首尾字符不同，使用max(左侧，下面)
                    dp[i][i + gap] = max(dp[i + 1][i + gap], dp[i][i + gap - 1]);
                }
            }
        }
        return dp[0][n-1];
    }
};