模拟弹簧振子的简谐振动

弹簧振子
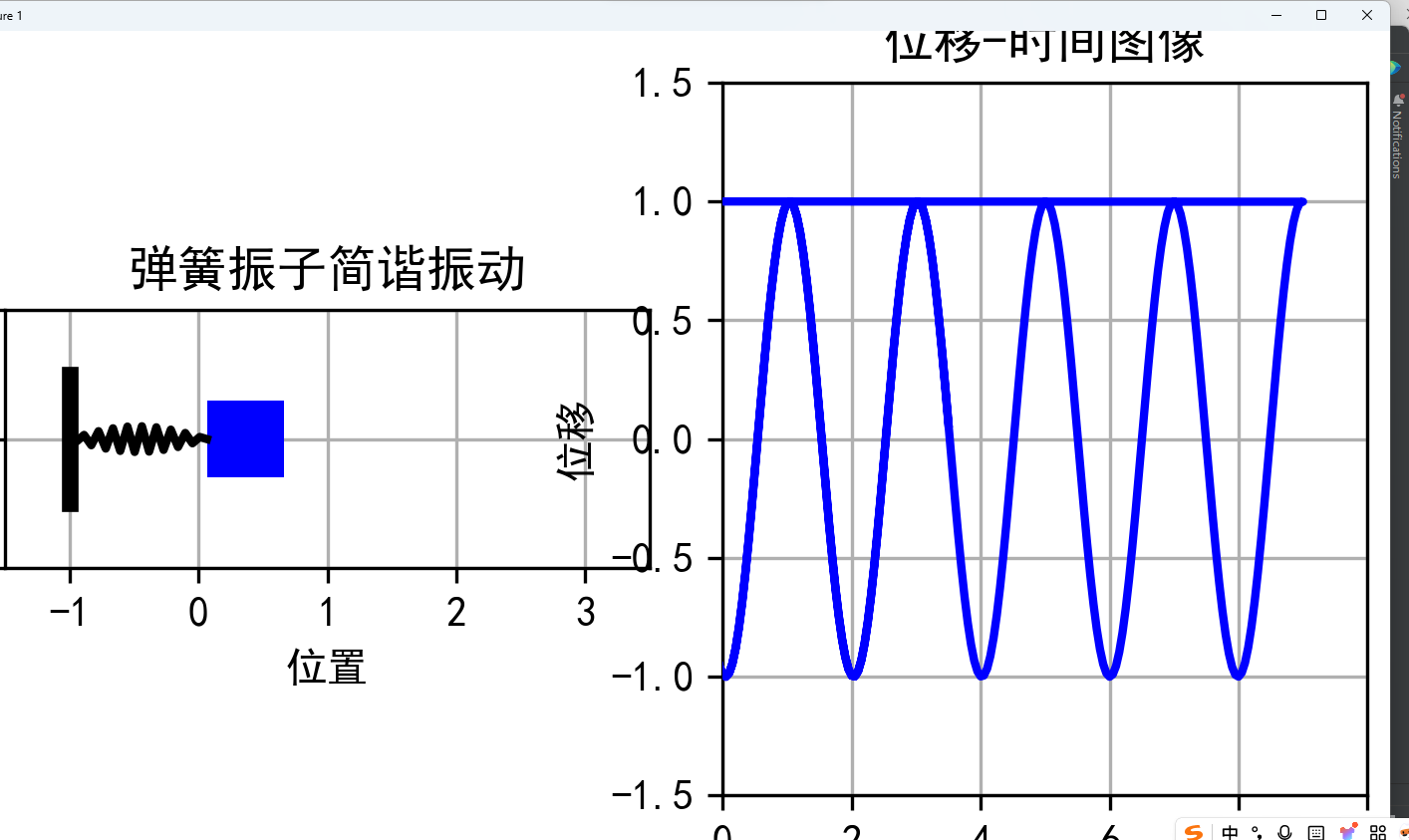
模拟弹簧振子的简谐振动，展示位移随时间的周期性变化及动画效果。

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from matplotlib.patches import Rectangle

# 设置图片清晰度
plt.rcParams['figure.dpi'] = 300

# 设置中文字体
plt.rcParams["font.family"] = ["SimHei", "WenQuanYi Micro Hei", "Heiti TC", "Microsoft YaHei"]
plt.rcParams["axes.unicode_minus"] = False  # 确保负号正确显示

# 创建画布和子图
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 6))
fig.subplots_adjust(wspace=0.3)

# 弹簧振子模拟区域
ax1.set_xlim(-1.5, 3.5)
ax1.set_ylim(-1, 1)
ax1.set_aspect('equal')
ax1.set_title('弹簧振子简谐振动')
ax1.set_xlabel('位置')
ax1.grid(True)

# 位移-时间图像
ax2.set_xlim(0, 10)
ax2.set_ylim(-1.5, 1.5)
ax2.set_title('位移-时间图像')
ax2.set_xlabel('时间')
ax2.set_ylabel('位移')
ax2.grid(True)

# 物理参数
m = 1.0  # 振子质量(kg)
k = 10.0  # 弹簧劲度系数(N/m)
x0 = 1.0  # 初始位移(m)
v0 = 0.0  # 初始速度(m/s)
omega = np.sqrt(k / m)  # 角频率
A = np.sqrt(x0 ** 2 + (v0 / omega) ** 2)  # 振幅
phi = np.arctan2(v0, omega * x0)  # 初相位

# 创建弹簧（用折线表示）
spring, = ax1.plot([], [], 'k-', lw=2)

# 创建振子（用矩形表示）
mass = Rectangle((0, -0.3), 0.6, 0.6, facecolor='blue')
ax1.add_patch(mass)

# 创建固定点
ax1.plot([-1, -1], [-0.5, 0.5], 'k-', lw=4)

# 位移-时间曲线
line, = ax2.plot([], [], 'b-', lw=2)
time_data, position_data = [], []


# 初始化函数
def init():
    spring.set_data([], [])
    mass.set_xy((0, -0.3))
    line.set_data([], [])
    return spring, mass, line


# 更新函数，用于动画每一帧的绘制
def update(frame):
    t = frame * 0.05  # 时间
    x = A * np.cos(omega * t + phi)  # 位移

    # 更新弹簧
    spring_x = np.linspace(-1, x, 20)
    spring_y = 0.1 * np.sin(np.linspace(0, 20 * np.pi, 20))
    spring.set_data(spring_x, spring_y)

    # 更新振子位置
    mass.set_xy((x, -0.3))

    # 更新位移-时间曲线
    time_data.append(t)
    position_data.append(x)
    line.set_data(time_data, position_data)

    # 自动调整x轴范围
    if t > 9:
        ax2.set_xlim(t - 9, t + 1)

    return spring, mass, line


# 创建动画
ani = FuncAnimation(fig, update, frames=range(200), init_func=init, interval=50, blit=True)

# 显示动画
plt.tight_layout()
plt.show()

# 如果需要保存动画，取消下面一行的注释
# ani.save('spring_oscillator.gif', writer='pillow', fps=20)