可解决的问题
逻辑回归主要用于解决分类问题,适用于标签取离散值的情况。既可以解决两类别分类,也可以解决多类别分类。
一、逻辑回归算法(Logistic Regression)
首先,对于两类别分类问题,将因变量(dependent variable)可能属于的两个类分别称为负向类(negative class)和正向类(positive class),则因变量 y ∈ 0 , 1 y \in0,1 y∈0,1,其中 0 表示负向类,1 表示正向类。
逻辑回归模型的假设是:
h
θ
(
x
)
=
g
(
θ
T
X
)
h_\theta(x)=g(\theta^TX)
hθ(x)=g(θTX),其中
X
X
X表示特征向量,
g
g
g 表示逻辑函数,常用的逻辑函数为 S 形函数(sigmod function)如下式:
g
(
z
)
=
1
1
+
e
−
z
g(z)=\frac{1}{1+e^{-z}}
g(z)=1+e−z1
g
(
z
)
g(z)
g(z) 函数图像如下所示:

函数 h θ ( x ) h_\theta(x) hθ(x)的作用是,对于给定的输入变量,根据选择的参数计算输出变量 y = 1 y=1 y=1 的可能性(estimated probablity),即 h θ ( x ) = P ( y = 1 ∣ x ; θ ) h_\theta(x)=P(y=1|x;\theta) hθ(x)=P(y=1∣x;θ)。
决策边界/判定边界(decision boundary): 是指标签分类的边界,对于两类别分类,可定义决策边界为:
当
h
θ
(
x
)
⩾
0.5
h_\theta(x)\geqslant0.5
hθ(x)⩾0.5 时,预测
y
=
1
y=1
y=1;
当
h
θ
(
x
)
<
0.5
h_\theta(x)<0.5
hθ(x)<0.5 时,预测
y
=
0
y=0
y=0。
则对于上述sigmod function,就有下式:
当
z
=
θ
T
X
⩾
0
z=\theta^TX\geqslant0
z=θTX⩾0 时,预测
y
=
1
y=1
y=1;
当
z
=
θ
T
X
<
0
z=\theta^TX<0
z=θTX<0 时,预测
y
=
0
y=0
y=0。
其中的
θ
T
X
\theta^TX
θTX 可以为线性的,也可以为非线性的。比如对于(i),就是线性的;对于(ii),就是非线性的。
(i).
θ
T
X
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
\theta^TX=\theta_0+\theta_1x_1+\theta_2x_2
θTX=θ0+θ1x1+θ2x2

(ii).
θ
T
X
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
θ
3
x
1
2
+
θ
4
x
2
2
\theta^TX=\theta_0+\theta_1x_1+\theta_2x_2+\theta_3x_1^2+\theta_4x_2^2
θTX=θ0+θ1x1+θ2x2+θ3x12+θ4x22

代价函数(cost function): 定义逻辑回归的代价函数为
J
(
θ
)
=
1
m
∑
i
=
1
m
C
o
s
t
(
h
θ
(
x
(
i
)
)
,
y
(
i
)
)
J(\theta)=\frac{1}{m}\sum_{i=1}^{m}Cost(h_{\theta}(x^{(i)}),y^{(i)})
J(θ)=m1∑i=1mCost(hθ(x(i)),y(i)),其中:
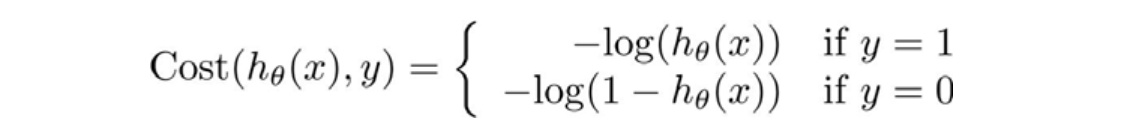
h
θ
(
x
)
h_\theta(x)
hθ(x)与
C
o
s
t
(
h
θ
(
x
)
,
y
)
Cost(h_{\theta}(x),y)
Cost(hθ(x),y)的关系如下图所示,

当
y
=
1
y=1
y=1 且
h
θ
(
x
)
=
1
h_\theta(x)=1
hθ(x)=1 时误差为 0;当
y
=
1
y=1
y=1 但
h
θ
(
x
)
h_\theta(x)
hθ(x) 不为1时,误差随着
h
θ
(
x
)
h_\theta(x)
hθ(x) 变小而变大;当
y
=
0
y=0
y=0 且
h
θ
(
x
)
=
0
h_\theta(x)=0
hθ(x)=0 时误差为0;当
y
=
0
y=0
y=0 但
h
θ
(
x
)
h_\theta(x)
hθ(x) 不为0时,误差随着
h
θ
(
x
)
h_\theta(x)
hθ(x) 变大而变大。将构建的
C
o
s
t
(
h
θ
(
x
)
,
y
)
Cost(h_{\theta}(x),y)
Cost(hθ(x),y) 简化如下:
C
o
s
t
(
h
θ
(
x
)
,
y
)
=
−
y
×
l
o
g
(
h
θ
(
x
)
)
−
(
1
−
y
)
×
l
o
g
(
1
−
h
θ
(
x
)
)
Cost(h_{\theta}(x),y)=-y\times log(h_\theta(x))-(1-y)\times log(1- h_\theta(x))
Cost(hθ(x),y)=−y×log(hθ(x))−(1−y)×log(1−hθ(x))
带入代价函数得到:
J
(
θ
)
=
1
m
∑
i
=
1
m
[
−
y
(
i
)
l
o
g
(
h
θ
(
x
(
i
)
)
)
−
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
]
=
−
1
m
∑
i
=
1
m
[
y
(
i
)
l
o
g
(
h
θ
(
x
(
i
)
)
)
+
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
]
J(\theta)=\frac{1}{m}\sum_{i=1}^{m}[-y^{(i)} log(h_\theta(x^{(i)}))-(1-y^{(i)})log(1- h_\theta(x^{(i)}))] \\ \ \ \ \ \ \ \ \ =-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)} log(h_\theta(x^{(i)}))+(1-y^{(i)}) log(1- h_\theta(x^{(i)}))]
J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))] =−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
通过梯度下降算法来求得使得代价函数最小的参数,即根据下式来更新参数
θ
\theta
θ:
θ
j
:
=
θ
j
−
α
∂
J
(
θ
)
∂
θ
j
\theta_j:=\theta_j-\alpha \frac{\partial J(\theta)}{\partial\theta_j}
θj:=θj−α∂θj∂J(θ)
推导过程如下:

最终的式子为:
θ
j
:
=
θ
j
−
α
1
m
∑
i
=
1
m
[
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
]
\theta_j:=\theta_j-\alpha \frac{1}{m} \sum_{i=1}^{m}[(h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)}]
θj:=θj−αm1i=1∑m[(hθ(x(i))−y(i))xj(i)]
虽然上式表面看与线性回归的梯度下降算法一样,但是这里的
h
θ
(
x
)
=
g
(
θ
T
X
)
h_\theta(x)=g(\theta^TX)
hθ(x)=g(θTX)与线性回归中的不同,所以实际上不一样。
线性回归:
h
θ
(
x
)
=
θ
T
X
=
θ
0
x
0
+
θ
1
x
1
+
θ
2
x
2
+
⋯
+
θ
n
x
n
h_\theta(x)=\theta^TX=\theta_0x_0+\theta_1x_1+\theta_2x_2+\cdots+\theta_nx_n
hθ(x)=θTX=θ0x0+θ1x1+θ2x2+⋯+θnxn
逻辑回归:
h
θ
(
x
)
=
1
1
+
e
−
θ
T
X
h_\theta(x)=\frac{1}{1+e^{-\theta^TX}}
hθ(x)=1+e−θTX1
多类别分类
上述讲的都是关于两类别分类,对于多类别分类也可以用逻辑回归解决。为了实现从“一对二”到“一对多”的转变,将多个类中的一个类标记为正向类(
y
=
1
y=1
y=1),然后将其他所有类都标记为负向类,将这个模型记作
h
θ
(
1
)
(
x
)
h_\theta^{(1)}(x)
hθ(1)(x);接着,类似地选择另一个类标记为正向类(
y
=
2
y=2
y=2),再将其它类都标记为负向类,将这个模型记作
h
θ
(
2
)
(
x
)
h_\theta^{(2)}(x)
hθ(2)(x),以此类推。最后得到一系列的模型简记为:
h
θ
(
i
)
(
x
)
=
P
(
y
=
i
∣
x
;
θ
)
,
i
=
(
1
,
2
,
⋯
,
k
)
h_\theta^{(i)}(x)=P(y=i|x;\theta),i=(1,2,\cdots,k)
hθ(i)(x)=P(y=i∣x;θ),i=(1,2,⋯,k)。
最后,在我们需要做预测时,将所有的分类机都运行一遍,然后对每一个输入变量
x
x
x,都选择最高可能性的输出变量
h
θ
(
i
)
(
x
)
h_\theta^{(i)}(x)
hθ(i)(x)。
将这些都做完之后,应该做的就是训练这个逻辑回归分类器:
h
θ
(
i
)
(
x
)
h_\theta^{(i)}(x)
hθ(i)(x),其中
i
i
i 对应每一个可能的
y
=
i
y=i
y=i,最后,为了做出预测,我们输入一个新的值
x
x
x,用这个做预测。要做的就是在
k
k
k 个分类器里面输入
x
x
x,然后选择一个让
h
θ
(
i
)
(
x
)
h_\theta^{(i)}(x)
hθ(i)(x) 最大的
i
i
i,即
max
i
h
θ
(
i
)
(
x
)
\displaystyle\max_{i}h_\theta^{(i)}(x)
imaxhθ(i)(x)。
现在知道了基本的挑选分类器的方法,选择出哪一个分类器是可信度最高效果最好的,那么就可认为得到一个正确的分类,无论
i
i
i 值是多少,我们都有最高的概率值,我们预测
y
y
y 就是那个值。
正则化: 给代价函数加入正则项后得到:
J
(
θ
)
=
1
m
∑
i
=
1
m
[
−
y
(
i
)
l
o
g
(
h
θ
(
x
(
i
)
)
)
−
(
1
−
y
(
i
)
)
l
o
g
(
1
−
h
θ
(
x
(
i
)
)
)
]
+
λ
2
m
∑
j
=
1
n
θ
j
2
J(\theta)=\frac{1}{m}\sum_{i=1}^{m}[-y^{(i)} log(h_\theta(x^{(i)}))-(1-y^{(i)})log(1- h_\theta(x^{(i)}))]+\frac{\lambda}{2m}\sum_{j=1}^n\theta_j^2
J(θ)=m1i=1∑m[−y(i)log(hθ(x(i)))−(1−y(i))log(1−hθ(x(i)))]+2mλj=1∑nθj2
求导后,对应的梯度下降算法公式为:
θ
0
:
=
θ
0
−
α
1
m
∑
i
=
1
m
[
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
0
(
i
)
]
θ
j
:
=
θ
j
−
α
[
1
m
∑
i
=
1
m
(
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
x
j
(
i
)
)
+
λ
m
θ
j
]
,
f
o
r
j
=
1
,
2
,
⋯
,
n
.
\theta_0:=\theta_0-\alpha \frac{1}{m} \sum_{i=1}^{m}[(h_{\theta}(x^{(i)})-y^{(i)})x_0^{(i)}] \\ \theta_j:=\theta_j-\alpha [\frac{1}{m} \sum_{i=1}^{m}((h_{\theta}(x^{(i)})-y^{(i)})x_j^{(i)})+\frac{\lambda}{m}\theta_j], for \ j=1,2,\cdots,n.
θ0:=θ0−αm1i=1∑m[(hθ(x(i))−y(i))x0(i)]θj:=θj−α[m1i=1∑m((hθ(x(i))−y(i))xj(i))+mλθj],for j=1,2,⋯,n.
二、Python代码实现
import pandas as pd
import numpy as np
def sigmoid(z):
return 1 / (1 + np.exp(-z))
'''
梯度下降
X:训练集
y:训练集标签
alpha:梯度下降学习率
n_estimate:训练次数
'''
def gradDescent(X,y):
m,n = X.shape
#将数据矩阵化
X = np.mat(X)
y = np.mat(y)
y = y.transpose()
#学习率设为0.01
alpha = 0.01
#进行500次训练,迭代更新权重矩阵
n_estimate = 500
#初始化一个值都为1的权重矩阵
weights = np.ones((n,1))
for k in range(n_estimate):
h = sigmoid(X * weights)
error = h - y
weights = weights - alpha * X.transpose() * error
return weights
'''
加载数据
'''
def loadData():
df = pd.read_csv('iris.csv')
#数据乱序
df = df.sample(frac=1)#抽取全部数据
#按照8:2的比例分隔数据,分别用来训练和测试
train_data = df[0:round(len(df)*0.8)] #round返回浮点数的四舍五入值
test_data = df[round(len(df)*0.8):]
y_train = train_data['LABEL']
X_train = train_data.drop('LABEL',axis=1)
y_test = test_data['LABEL']
X_test = test_data.drop('LABEL', axis=1)
#矩阵化测试集
X_test = np.mat(X_test)
#数组化测试集的label
y_test = y_test.tolist()
return X_train,y_train,X_test,y_test
if __name__ == '__main__':
X_train, y_train, X_test, y_test = loadData()
weights = gradDescent(X_train, y_train)
#别忘了要乘上sigmoid函数
X_predict = sigmoid(X_test * weights)
#将数据从二维矩阵转为数组
X_predict = X_predict.tolist()
for i in range(len(X_predict)):
x = X_predict[i] #预测值
y = y_test[i] #真实值
prob_of_one = x[0]
if prob_of_one >= 0.5:
print('predict: 1 , ' + 'actual: ' + str(y))
else:
print('predict: 0 , ' + 'actual: ' + str(y))






















 173
173











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








