语音信号处理五——求线性时不变系统卷积和的解

---

前言

上一篇文章中介绍了LTI系统的含义，以及它的特征，同时对于LTI系统，使用单位冲激分解和单位冲激响应推导出了在时域上，分析LTI系统的重要工具——卷积和
$$y(n)=\sum _{k=-\infty }^{\infty }x(k)h(n-k)$$
也写作
$$y(n)=x(n)\ast h(n)$$

那么这一篇中，将会有很多实例来利用卷积公式，进行实际的计算卷积公式的解。

|版本声明：山河君，未经博主允许，禁止转载

---

一、卷积和的解

1.含义

卷积公式的解是指：在给定一定的信号和系统的冲激响应，通过卷积公式获取最终的输出。

2.卷积公式的分析

1）使用m代替k

对于单位冲激分解和卷积公式来说
$$x(n)=\sum _{k=-\infty }^{\infty }x(k)\delta [n-k]$$
$$y(n)=x(n)\ast h(n)=\sum _{k=-\infty }^{\infty }x(k)h(n-k)$$
单位冲激分解中的$k$，可以看作$n=k$时，$x(k)$作为权系数才对系统的输入有贡献。
而在卷积公式中的$k$，可以看作$h(n-k)=\tau [\delta (n-k)]$，对于单位冲激响应的偏移。
为了便于区分，现在使用$m$来代表$k$在接下来的运算。

• 对于$m$时刻的冲激响应，先进行反转得到$h(-m)$
• 再将$h(-m)$进行移位$n$，就得到$h(n-m)$，即当$n>0$，序列右移，反之，序列左移
• 即卷积公式可以看作是$x(m)$与$h(n-m)$的相乘相加后得到$y(n)$

2）理解m的作用

从上面使用$m$代替$k$看起来好像没有实际的必要，实际上在求LTI的卷积和的解时，我们通常会使用图解法、解析法和一些其他工具例如matlab的工具箱来进行分析，下面以实际图解例子来理解一下为什么要使用$m$进行翻转。

假设：$x(n)=R_4(n),h(n)=R_4(n)$，其中$R_4$代表的是长度为4的单位越阶信号， 那么$y(n)=x(n)\ast h(n)?$

解：

• 根据$x(n)=R_4(n),h(n)=R_4(n)$，可以看到图像
  

• 根据条件可知，$0\le n\le 3$，同时单位冲激响应范围也是$0\le (n-m)\le 3$，即两边加$n$再翻转就得到了$m$的取值范围：$n-3\le m\le n$。

• 此时将$m$进行翻转可得，$-3\le -m\le 0$，我们之前说加上$n$，当$n>0$，序列右移，反之，序列左移，那么图像看起来如下：
  

• 由此我们看到，当$n=0$时，卷积公式中只有$h(0)$处对于系统的输出有贡献，而当$n=1$时，则$h(0)，h(1)$对于系统的输出都有贡献，而最终的系统输出使用数学描述：
  $n=0,y(0)=R_4(0)\ast R_4(0)=1$
  $n=1,y(1)=R_4(0)\ast R_4(1)+R_4(1)\ast R_4(0)=2$
  $n=2,y(2)=R_4(0)\ast R_4(2)+R_4(1)\ast R_4(1)+R_4(2)\ast R_4(0)=3$
  $n=3,y(3)=R_4(0)\ast R_4(3)+R_4(1)\ast R_4(2)+R_4(2)\ast R_4(1)+R_4(3)\ast R_4(0)=4$
  $n=4,y(4)=R_4(1)\ast R_4(3)+R_4(2)\ast R_4(2)+R_4(3)\ast R_4(1)=3$
  $n=5,y(5)=R_4(2)\ast R_4(3)+R_4(3)\ast R_4(2)=2$
  $n=6,y(6)=R_4(3)\ast R_4(3)=1$
  

3.卷积结果的长度

卷积结果的长度也就是系统输出$y(n)$的长度，我们使用$L_x$和$L_h$表示系统输入的长度和单位冲激响应的长度，那么卷积结果的长度为$L_x+L_h-1$，也就是说系统的输出在$n=L_x+L_h-1$处有值。下面就是求出长度的推导过程

对于卷积公式$y(n)=x(n)\ast h(n)={\sum }_{k=-\infty }^{\infty }x(k)h(n-k)$，我们使用$L_x$和$L_h$表示系统输入的长度和单位冲激响应的长度，也就是说：
$x(n)$长度为$L_x$，即$x(n)\ne 0,0\le n<L_x(\le L_x-1)$
$h(n)$长度为$L_h$，即$h(n)\ne 0,0\le n<L_h(\le L_h-1)$

由卷积公式可知，卷积运算过程中每一项如果有值，那么就要求$x(m)$和$h(n-m)$都不为0，针对于$x(m),m\in [0,L_x-1]$，针对于$h(n-m),n\in [m,m+L_h-1]$

• 卷积的起点
  针对于$x(m)$，要求$x(m)\ne 0$，因此卷积的起点为0
• 卷积的终点
  针对于$h(n-m)\ne 0$，而$x(m),m\in [0,L_x-1]$，$n$的最大值（当$m=m_{max}=L_x-1$时$n$最大）为$L_x-1+L_h-1=L_x+L_h-2$，因为是从0开始，所以卷积的长度为$L_x+L_h-1$

由此，在上文中提到的例子又可以拆分为
$0\le n\le 3,y(n)={\sum }_{m=0}^{n}1=n+1$
$4\le n\le 6,y(n)={\sum }_{n-3}^{3}1=7-n$
$$y(n)=\{\begin{array}{l}n+1,0\le n\le 3\\ 7-n,4\le n\le 6\\ 0,0\end{array}$$
从上文中对于卷积求解的例子中可以看出，对于系统的输入第一个信号$R_4(0)$影响了前L个输出，而系统输入的最后一个信号$R_4(3)$影响到了最后L个输出。对于为什么系统的输出会变长的理解，可以看上一章音频进阶学习四——线性时不变系统之卷积和。

二、卷积和的性质

1.卷积和性质

卷积公式拥有以下性质：

• 交换律：$x(n)\ast h(n)=h(n)\ast x(n)=>{\sum }_{k=-\infty }^{\infty }x(k)h(n-k)={\sum }_{k=-\infty }^{\infty }x(n-k)h(n)$
• 结合律：$x(n)\ast [h_1(n)\ast h_2(n)]=[x(n)\ast h_1(n)]\ast h_2(n)$
• 分配律：$x(n)\ast [h_1(n)+h_2(n)]=x(n)\ast h_1(n)+x(n)\ast h_2(n)$

注意：非线性系统或者时变系统，以上性质不成立

2.利用图像理解卷积和的性质

• 交换律：图a等于图b
  
  
• 结合律：图c等于图d
  
  
• 分配律：图e等于图f
  
  

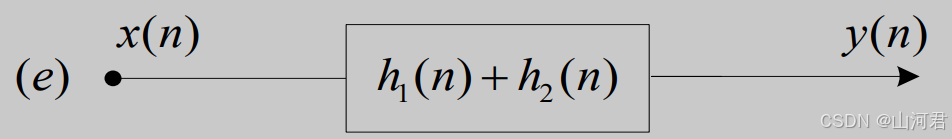
3.卷积性质使用的实际列子

我们在之前的文章中有说过，系统的级联是将第一个系统的输出当作第二个系统的输入，假设两个系统都为LTI系统，如下图单位脉冲响应为$h_1(n)$和单位脉冲响应为$h_2(n)$的系统为级联：

设$x(n)=u(n),h_1(n)=\delta (n)-\delta (n-4),h_2(n)=a_{n}u(n)|a|<1,y(n)?$

• 让我们分析$h_1(n)$，如果对于单位冲激响应为$\delta (n)$，那么卷积公式有：$y(n)={\sum }_{m=-\infty }^{\infty }x(m)\delta (n-m)$，只有当$n=m,x(m)\ast \delta (n-m)\ne 0$时，输出才有值，且输出为：
  $$y(n)=x(n)\ast \delta (n)=x(k){|}_{k=n}=x(n)$$
  那么对于$h_1(n)$则有：
  $$\begin{gathered} m(n)=u(n)\ast [\delta (n)-\delta (n-4)]分配律 \\ =u(n)\ast \delta (n)-u(n)\ast \delta (n-4)交换律 \\ =u(n)-u(n-4) \end{gathered}$$
• 接着分析$m(n)$的范围，对于$u(n)$是单位越阶信号
  $$u(n)=\{\begin{array}{l}1,n\ge 0\\ 0,n<0\end{array}$$
  作为$h_2(n)$的输入，只有在$m(n)=1,n=0,1,2,3$才有输入，所以它是一个宽度为4的矩型信号，所以$m(n)=\delta (n)+\delta (n-1)+\delta (n-2)+\delta (n-3)$
• 分析$y(n)$的输出，将$m(n),h_2(n)$代入卷积公式有:
  $$\begin{gathered} y(n)=\sum _{k=-\infty }^{\infty }m(k)a_{n-k}u(n-k) \\ =m(n)\ast a_{n}u(n)=a_{n}u(n)\ast [\delta (n)+\delta (n-1)+\delta (n-2)+\delta (n-3)]分配律 \\ =a_{n}u(n)\ast \delta (n)+a_{n}u(n)\ast \delta (n-1)+a_{n}u(n)\ast \delta (n-2)+a_{n}u(n)\ast \delta (n-3)交换律 \\ =a_{n}u(n)+a_{n-1}u(n-1)+a_{n-2}u(n-2)+a_{n-3}u(n-3) \end{gathered}$$

---

总结

本章内容中先对于卷积公式结合一个简单的例子，通过给定的输入和单位冲激响应求出系统的输出，并得到其中一个结论为：卷积结果的长度为$L_x+L_h-1$。

接着结合实际的图像介绍了卷积的三大性质，通过三大性质结合实例求出卷积的解，下一章节中，会对于差分方程进行介绍，这是在时域中分析语音信号的另一个重要工具。

如果对您有所帮助，请帮忙点个赞吧！