scheme语言直译为汉语（十七）

一、符号数据

在这一节里，我们要扩充所用语言的表述能力，引进将任意符号作为作为数据的功能。

1. 引号

如果我们能构造出采用符号的复合数据，我们就可以有下面这类的表:

(abcd)
(23 45 17)
((Norah 12) (Molly 9) (Anna 7) (Lauren 6) (Charlotte 4))

这些包含着符号的表看起来就像是我们语言里的表达式:

(* (+ 23 45) (+ х 9))
(define (fact n) (if (= n 1) 1 (* n (fact (- n 1)))))

为了能够操作这些符号，我们的语言里就需要有一种新元素：为数据对象加引号的能力。假定我们希望构造出表(a b)， 当然不能用(list a b) 完成这件事，因为这一表达式将要构造出的是a和b的值的表，而不是这两个符号本身的表。在自然语言的环境中，这种情况也是众所周知的，在那里的单词和句子可能看作语义实体，也可以看作是字符的序列(语法实体)。在自然语言里，常见的方式就是用引号表明一个词或者一个句子应作为文字看待，将它们直接作为字符的序列。例如说，“John" 的第一个字母显然是“J”。如果我们对某人说“大声说你的名字”，此时希望听到的是那个人的名字。如果说“大声说‘你的名字’”，此时希望听到的就是词组“你的名字”。请注意，我们在这里不得不用嵌套的引号去描述别人应该说的东西。

我们可以按照同样的方式，将表和符号标记为应该作为数据对象看待，而不是作为应该求值的表达式。然而，这里所用的引号形式与自然语言中的不同，我们只在被引对象的前面放一个引号( 按照习惯，在这里用单引号)。在Scheme 里可以不写结束引号，因为这里已经靠空白和括号将对象分隔开，一个单引号的意义就是引用下一个对象。

现在我们就可以区分符号和它们的值了：

(define a 1)

(define b 2)

(list a b)
(1 2)

(list 'a 'b)
(a b)

(list 'a b)
(a 2)

尝试将上述过程直译为汉语：

（定义 甲 1）

（定义 乙 2）

（序列 甲 乙）
（1 2）

（序列 ‘甲 ’乙）
（甲 乙）

（序列 ‘甲 乙）
（甲 2）

引号也可以用于复合对象，其中采用的是表的方便的输出表示方式：

(car '(a b c))
a

(cdr '(a b c))
(b c)

尝试将上述过程直译为汉语：

（前头的项 ‘（甲 乙 丙））
 甲
（后面的项 ‘（甲 乙 丙））
（乙 丙）

记住这些之后，我们就可以通过求值’()得到空表，这样就可以丢掉变量nil了。

为了能对符号做各种操作，我们还需要用另一个基本过程eq?，这个过程以两个符号作为参数，检查它们是否为同样的符号。利用eq?可以实现一个称为memq的有用过程，它以一个符号和一个表为参数。如果这个符号不包含在这个表里(也就是说，它与表里的任何项目都不eq? )，memq就返回假；否则就返回该表的由这个符号的第一次出现开始的那个子表：

(define (memq item x)
    (cond ((null? x) false)
          ((eq? item (car x)) x)
          (else (memq item (cdr x)))))

（定义 （由某给定内容开始的子字符串 给定内容 字符串）
    （情况符合 （（到空值了？字符串）无）
             （（字符相同？给定内容 （前头的项 字符串））字符串）
             （否则 （由某给定内容开始的子字符串 给定内容 （后面的项 字符串）））））

举例来说，表达式：

(memq 'apple '(pear banana prune))

的值是假，而表达式：

(memq 'apple '(x (apple sauce) y apple pear))

的值是(apple pear)。

注：不返回（apple sauce）什么的应该和括号这个符号的特殊性有关。

练习2.53
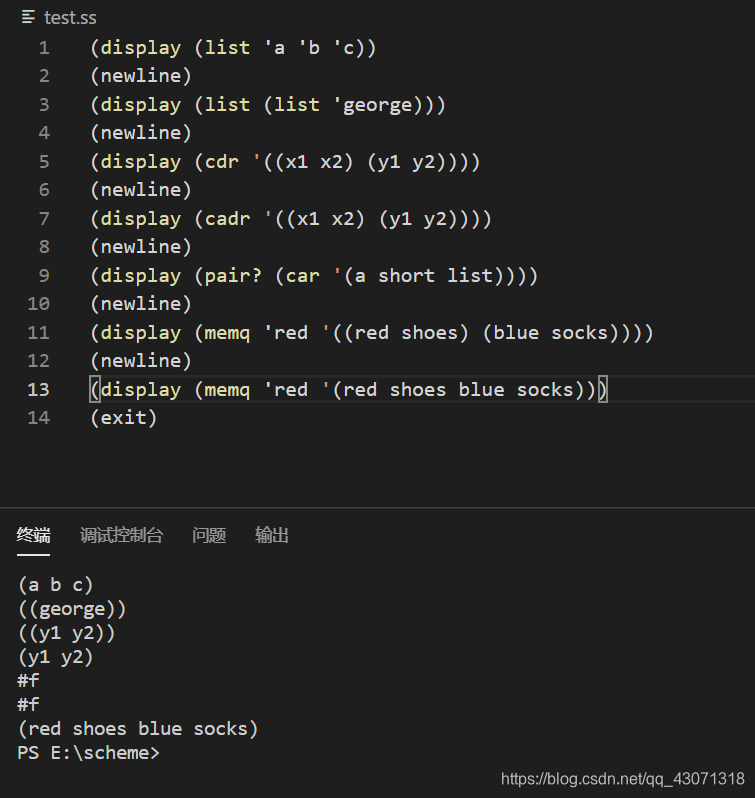
解释器在求值下面各个表达式时将打印出什么?

(list 'a 'b 'c)
(list (list 'george))
(cdr '((x1 x2) (y1 y2)))
(cadr '((x1 x2) (y1 y2)))
(pair? (car '(a short list)))
(memq 'red '((red shoes) (blue socks)))
(memq 'red '(red shoes blue socks))

解：

练习2.54
如果两个表包含着同样元素，这些元素也按同样顺序排列，那么就称这两个表equal?。例如:

(equal? '(this is a list) '(this is a list))

是真，而

(equa1? '(this is a list) '(this (is a) list))

是假。说得更准确些，我们可以从符号相等的基本eq?出发，以递归方式定义出equal?。a和b是equal?的，如果它们都是符号，而且这两个符号满足eq?；或者它们都是表，而且(car a)和(car b)相互equal?，它们的(cdr a)和(cdr b)也是equal?。请利用这一思路定义出equal?过程。
解：

(define (equal? a b)
    (cond ((and (not (pair? a)) (not (pair? b))) (eq? a b))
          ((and (pair? a) (pair? b))
           (and (eq? (car a) (car b))
                (equal? (cdr a) (cdr b))))
          (else false)))

尝试把上述过程直译为汉语：

（定义 （语句相等？ 甲 乙）
    （情况符合 （（与 （不 （成对？ 甲））（不 （成对？ 乙）））（元素相等？ 甲 乙））
             （（与 （成对？ 甲）（成对？ 乙））
              （与 （元素相等？ （前头的项 甲）（前头的项 乙））
                  （语句相等？ （后面的项 甲）（后面的项 乙））））
             （其它情况 不等）））;这最后一行的“不等”以后应该再进一步思考

练习2.55
Eva Lu Ator输入了表达式:

(car ’’ abracadabra)

令她吃惊的是解释器打印出的是quote。请解释这一情况。
解：
由于 ’ 实际是 quote 过程，即 'abracadabra 为 (quote abracadabra)，因此 (car ''abracadabra) 为 (car '(quote abracadabra))，会输出 quote。

2.实例：符号求导

考虑一个简化的求导程序，其处理的表达式都是由对于两个参数的加和乘运算构造起来的。对于这种表达式的求导可以通过下面几条归约规则完成：
$$\begin{array}{rl}\frac{dc}{dx}& =0当c是一个常量，或者一个与x不同的变量\\ \frac{dx}{dx}& =1\\ \frac{d(u+v)}{dx}& =\frac{du}{dx}+\frac{dv}{dx}\\ \frac{d(uv)}{dx}& =u(\frac{dv}{dx})+v(\frac{du}{dx})\end{array}$$
那为了能使用上述几条规则，用一下按愿望思维，我们需要下面这些抽象出来的小语句：

(variable? e)               e是变量吗？
(same-variable? v1 v2)      v1和v2是同一个变量吗？   
(sum? e)                    e是和式吗？ 
(addend e)                  e的被加数
(augend e)                  e的加数
(make-sum a1 a2)            构造起a1与a2的和式

(product? e)                e是乘式吗？
(multiplier e)              e的被乘数
(multiplicand e)            e的乘数
(make-product m1 m2)        构造起m1与m2的乘式

尝试把上述过程直译为汉语：

（是变量？ 整式）
（是同一个变量？ 甲 乙）
（是和式？ 整式）
（被加数 整式）
（加数 整式）
（构造和式 被加数 加数）

（是乘式？ 整式）
（被乘数 整式）
（乘数 整式）
（构造乘式 被乘数 乘数）

利用这些过程，以及判断表达式是否数值的基本过程number?，我们就可以将各种求导规则用下面的过程表达出来了：

(define (derive exp var)
    (cond ((number? exp) 0)
          ((variable? exp)
           (if (same-variable? exp var) 
               1 
               0))
          ((sum? exp)
           (make-sum (deriv (addend exp) var)
                     (deriv (augend exp) var)))
          ((product? exp)
           (make-sum
               (make-product (multiplier exp)
                             (deriv (multiplicand exp) var))
               (make-product (deriv (multiplier exp) var))
                             (multiplicand exp))))
          (else
           (error "unknown expression type -- DERIV" exp))))

尝试把上述过程直译为汉语：

(定义 (导数 表达式 变量)
    (情况符合 ((是数字? 表达式) 0)
             ((是单一变量? 表达式)
              (如果 (是同一个变量? 表达式 变量) 
                    1 
                    0))
             ((是和式? 表达式)
              (构造和式 (导数 (被加数 表达式) 变量)
                       (导数 (加数 表达式) 变量)))
             ((是乘式? 表达式)
              (构造和式
                 (构造乘式 (被乘数 表达式)
                          (导数 (乘数 表达式) 变量))
                 (构造乘式 (导数 (被乘数 表达式) 变量))
                          (乘数 表达式))))
          (其它情况
           (错误 "这个表达式至少在我们这个程序中不可导，不合法" 表达式))))

过程deriv里包含了一个完整的求导算法。因为它是基于抽象数据表述的，因此，无论我们如何选择代数表达式的具体表示，只要设计了一组正确的选择函数和构造函数，这个过程都可以工作。表示的问题是下面必须考虑的问题。

代数表达式的表示

我们可以设想出许多用表结构表示代数表达式的方法。例如，可以利用符号的表去直接反应代数的记法形式，将表达式ax+b表示为表(a * x + b)。然而，一种特别直截了当的选择，是采用Lisp里面表示组合式的那种带括号的前缀形式，也就是说，将ax+b表示为(+(*ax)b)。这样，我们有关求导问题的数据表示就是：

●变量就是符号，它们可以用基本谓词symbol?判断:

(define (variable? x) (symbol? x))

●两个变量相同就是表示它们的符号相互eq?:

(define (same-variable? v1 v2)
    (and (variable? v1) (variable? v2) (eq? v1 v2)))

●和式与乘式都构造为表:

(define (make-sum a1 a2) (list '+ al a2))
(define (make-product m1 m2) (list '* m1 m2))

●和式就是第一个元素为符号+的表:

(define (sum? x)
    (and (pair? x) (eq? (car x) '+)))

●被加数是表示和式的表里的第二个元素:

(define (addend s) (cadr s))

●加数是表示和式的表里的第三个元素:

(define (augend s) (caddr s))

●乘式就是第一个元素为符号 * 的表:

(define (product? x)
    (and (pair? x) (eq? (car x) '*)))

●被乘数是表示乘式的表里的第二个元素:

(define (multiplier p) (cadr p))

●乘数是表示乘式的表里的第三个元素:

(define (multiplicand p) (caddr p))

这样，为了得到一个能够工作的符号求导程序，我们只需将这些过程与deriv装在一起。现在让我们看几个表现这一程序的行为的实例：

(deriv '(+ x 3) 'x)
(+ 1 0)

(deriv '(* x y) 'x)
(+ (* x 0) (* 1 y))

(deriv '(* x y) 'x)
(+ (* x 0) (* 1 y))

(deriv '(* (* x y) (+ x 3)) 'x)
(+ (* (* x y) (+ 1 0))
   (* (+ (* x y) (* 1 y))
      (+ x 3)))

程序产生出的这些结果是对的，但是它们没有经过化简。我们确实有：
$$\frac{d(xy)}{dx}=x\cdot 0+1\cdot y$$
当然，我们也可能希望这一程序能够知道$x\cdot 0=0$, $1\cdot y=y$以及$0+y=y$。因此，第二个例子的结果就应该是简单的y。正如上面的第三个例子所显示的，当表达式变得更加复杂时，这一情况也可能变成严重的问题。

现在所面临的困难很像我们在做有理数首先时所遇到的问题:希望将结果化简到最简单的形式。为了完成有理数的化简，我们只需要修改构造函数和选择函数的实现。这里也可以采取同样的策略。我们在这里也完全不必修改deriv,只需要修改make-sum,使得当两个求和对象都是数时，make-sum求出它们的和返回。还有，如果其中的一个求和对象是0，那么make-sum就直接返回另一个对象。

(define (make-sum a1 a2)
    (cond ((=number? a1 0) a2)
          ((=number? a2 0) a1)
          ((and (number? a1) (number? a2)) (+ a1 a2))
          (else (list '+ a1 a2))))

尝试将上述过程直译为汉语：

（定义 （构造和式 被加数 加数）
    （情况符合）（（等于给定值？ 被加数 0）加数）
              （（等于给定值？ 加数 0）被加数）
              （（与 （是数字？ 被加数）（是数字？加数））（+ 被加数 加数））
              （其它情况 （序列 ‘+ 被加数 加数）））

在这个实现里用到了过程=number?，它检查某个表达式是否等于一个给定的数。

(define (=number? exp num)
    (and (number? exp) (= exp num)))

尝试将上述过程直译为汉语：

（定义 （等于给定值？ 表达式 值）
    （与 （是数字？ 表达式）（= 表达式 值）））

与此类似，我们也需要修改make-product，设法引进下面的规则：0与任何东西的乘积都是0，1与任何东西的乘积总是那个东西：

(define (make-product m1 m2)
    (cond ((or (=number? m1 0) (=number? m2 0)) 0)
          ((=number? m1 1) m2)
          ((=number? m2 1) m1)
          ((and (number? m1) (number? m2)) (* m1 m2))
          (else (list '* m1 m2))))

（定义 （构造乘式 被乘数 乘数）
    （情况符合）（（或 （等于给定值？ 被乘数 0）（等于给定值？ 乘数 0））0）
              （（等于给定值？ 被乘数 1）乘数）
              （（等于给定值？ 乘数 1）被乘数）
              （（与 （是数字？ 被乘数） （是数字？ 乘数）） （* 被乘数 乘数））
              （其它情况 （序列 ‘* 被乘数 乘数））））

下面是这一新过程版本对前面三个例子的结果：

(deriv '(+ x 3) 'x)
1

(deriv '(* x y) 'x)
y

(deriv '(* (* x y) (+ x 3)) 'x)
(+ (* x y) (* y (+ x 3)))

（导数 ‘（+ 线 3）’线）
1

（导数 ‘（* 线 面）’线）
面

（导数 ‘（* （* 线 面）（+ 线 3））’线）
（+ （* 线 面）（* 面 （+ 线 3）））

显然情况已经大大改观。但是，第三个例子还是说明，要想做出一一个程序，使它能将表达式做成我们都能同意的“最简单”形式，前面还有很长的路要走。代数化简是一个非常复杂的问题，除了其他各种因素之外，还有另一个根本性的问题:对于某种用途的最简形式，对于另一用途可能就不是最简形式。

练习2.56
请说明如何扩充基本求导规则，以便能够处理更多种类的表达式。例如，通过给程序deriv增加-一个新子句，并以适当方式定义过程exponentiation?、base、exponent和make-exponentiation的方式，实现下述求导规则(你可以考虑用符号**表示乘幂)：
$$\frac{d(u^n)}{dx}=n{u}^{n-1}(\frac{du}{dx})$$
请将如下规则也构造到程序里:任何东西的0次幂都是1，而它们的1次幂都是其自身。

解：

(define (** base exponent)
    (define (iter exponent r)
        (if (= exponent 0)
            r
            (iter (- exponent 1) (* r base))))
    (iter exponent 1))

(define (exponentiation? exp)
    (and (pair? exp) (eq? (car exp) '**)))
(define (=number? exp num)
    (and (number? exp) (= exp num)))
(define (make-exponentiation base exponent)
    (cond ((=number? exponent 0) 1)
          ((=number? exponent 1) base)
          ((and (number? base) (number? exponent)) (** base exponent))
          (else (list '** base exponent))))
(define (base exp)
    (cadr exp))
(define (exponent exp)
    (caddr exp))
(define (variable? x) (symbol? x))
(define (same-variable? v1 v2)
    (and (variable? v1) (variable? v2) (eq? v1 v2)))
(define (make-sum a1 a2)
  (cond ((=number? a1 0) a2)
        ((=number? a2 0) a1)
        ((and (number? a1) (number? a2)) (+ a1 a2))
        (else (list '+ a1 a2))))

(define (make-product m1 m2)
  (cond ((or (=number? m1 0) (=number? m2 0)) 0)
        ((=number? m1 1) m2)
        ((=number? m2 1) m1)
        ((and (number? m1) (number? m2)) (* m1 m2))
        (else (list '* m1 m2))))
(define (sum? x)
    (and (pair? x) (eq? (car x) '+)))
(define (addend s) (cadr s))
(define (augend s) (caddr s))
(define (product? x)
    (and (pair? x) (eq? (car x) '*)))
(define (multiplier p) (cadr p))
(define (multiplicand p) (caddr p))
(define (deriv exp var)
    (cond ((number? exp) 0)
          ((variable? exp)
           (if (same-variable? exp var) 
               1 
               0))
          ((sum? exp)
           (make-sum (deriv (addend exp) var)
                     (deriv (augend exp) var)))
          ((product? exp)
           (make-sum
               (make-product (multiplier exp)
                             (deriv (multiplicand exp) var))
               (make-product (deriv (multiplier exp) var)
                             (multiplicand exp))))
          ((exponentiation? exp)
               (make-product (exponent exp) 
                             (make-exponentiation (base exp) (- (exponent exp) 1))))
          (else
           (error "unknown expression type -- DERIV" exp))))
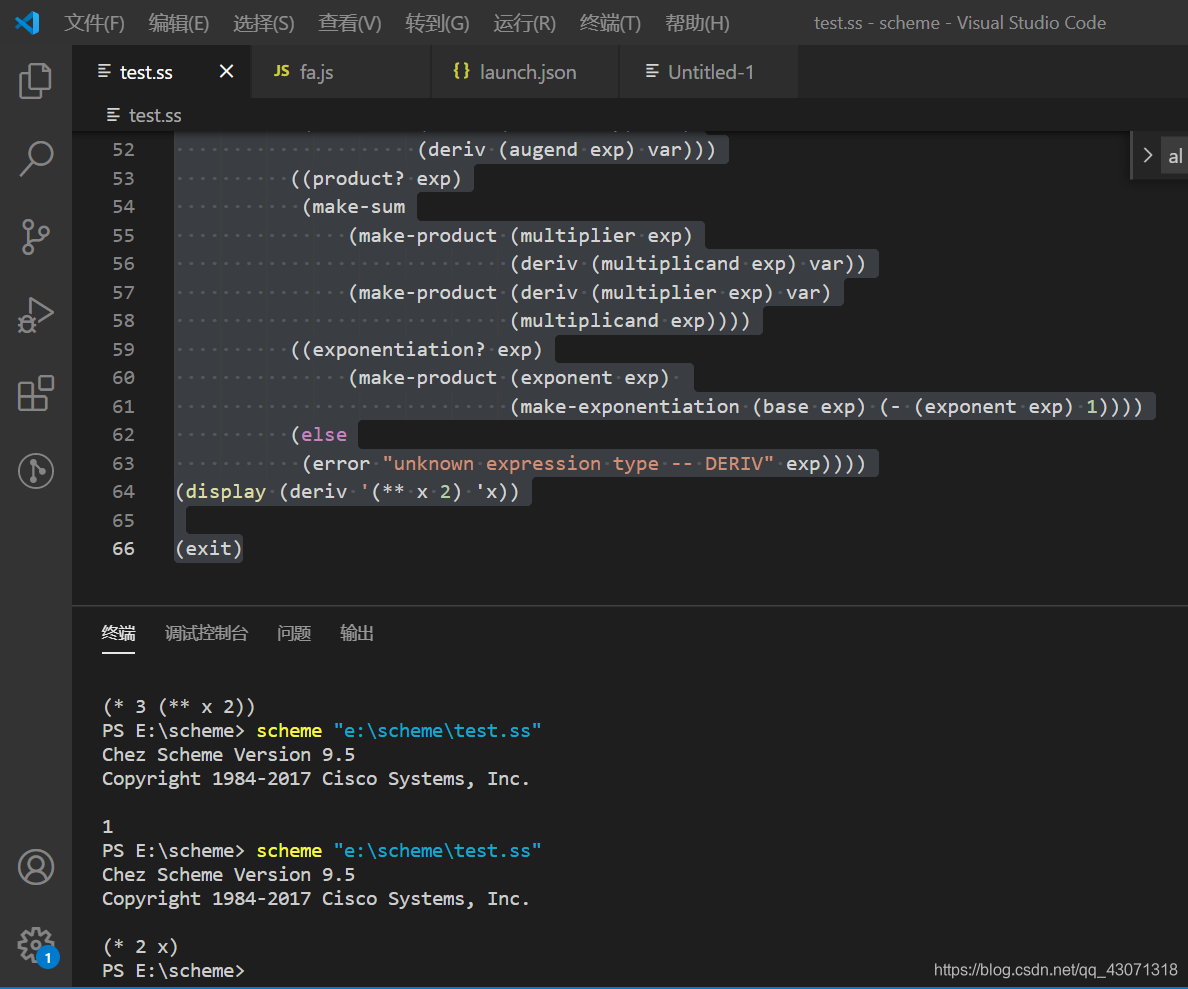
(display (deriv '(** x 2) 'x))

(exit)

这题我实在是忍不住想用汉语做变量名及函数名了：

(define (是数字？ 元) (number? 元))
(define (第一项 序列) (car 序列))
(define (第二项 序列) (cadr 序列))
(define (第三项 序列) (caddr 序列))
(define (成对？ 元) (pair? 元))
(define (同样？ 甲 乙) (eq? 甲 乙))
(define (是变量？ 表达式) (symbol? 表达式))
(define (是同一个变量？ 甲 乙) 
    (and (是变量？ 甲) (是变量？ 乙) (等于？ 甲 乙)))
(define (等于给定值？ 元 给定值)
    (and (是数字？ 元) (等于？ 元 给定值)))
(define (构造和式 被加数 加数)
    (cond ((等于给定值？ 被加数 0) 加数)
          ((等于给定值？ 加数 0) 被加数)
          ((and (是数字？被加数) (是数字？加数)) (+ 被加数 加数))
          (else (list '+ 被加数 加数))))
(define (构造乘式 被乘数 乘数)
    (cond ((等于给定值？ 被乘数 1) 乘数)
          ((等于给定值？ 乘数 1) 被乘数)
          ((or (等于给定值？ 被乘数 0) (等于给定值？ 乘数 0)) 0)
          ((and (是数字？ 被乘数) (是数字？ 乘数)) (* 被乘数 乘数))
          (else (list '* 被乘数 乘数))))
(define (构造指数式 底数 指数)
    (cond ((等于给定值？ 指数 1) 底数)
          ((等于给定值？ 指数 0) 1)
          ((and (是数字？ 底数) (是数字？ 指数)) (** 底数 指数))
          (else (list '** 底数 指数))))
(define (是和式？ 表达式)
    (and (成对？ 表达式) (同样？ (第一项 表达式) '+)))
(define (是乘式？ 表达式)
    (and (成对？ 表达式) (同样？ (第一项 表达式) '*)))
(define (是指数式？ 表达式)
    (and (成对？ 表达式) (同样？ (第一项 表达式) '**)))
(define (被加数 表达式)
    (第二项 表达式))
(define (加数 表达式)
    (第三项 表达式))
(define (被乘数 表达式)
    (第二项 表达式))
(define (乘数 表达式)
    (第三项 表达式))
(define (底数 表达式)
    (第二项 表达式))
(define (指数 表达式)
    (第三项 表达式))
(define (** 底数 指数)
    (define (乘方迭代器 指数 乘方结果)
        (if (= 指数 0) 
            乘方结果
            (乘方迭代器 (- 指数 1) (* 乘方结果 底数))))
    (乘方迭代器 指数 1))


(define (导数 表达式 变量)
    (cond ((是数字？ 表达式) 0)
          ((是变量？ 表达式)
           (if (是同一个变量？ 表达式 变量) 
               1 
               0))
          ((是和式？ 表达式)
           (构造和式 (导数 (被加数 表达式) 变量)
                    (导数 (加数 表达式) 变量)))
          ((是乘式？ 表达式)
           (构造和式
               (构造乘式 (乘数 表达式)
                        (导数 (被乘数 表达式) 变量))
               (构造乘式 (导数 (乘数 表达式) 变量)
                        (被乘数 表达式))))
          ((是指数式？ 表达式)
               (构造乘式 (指数 表达式) 
                        (构造指数式 (底数 表达式) (- (指数 表达式) 1))))
          (else
           (error "这个表达式在咱这不可导，不合法" 表达式))))
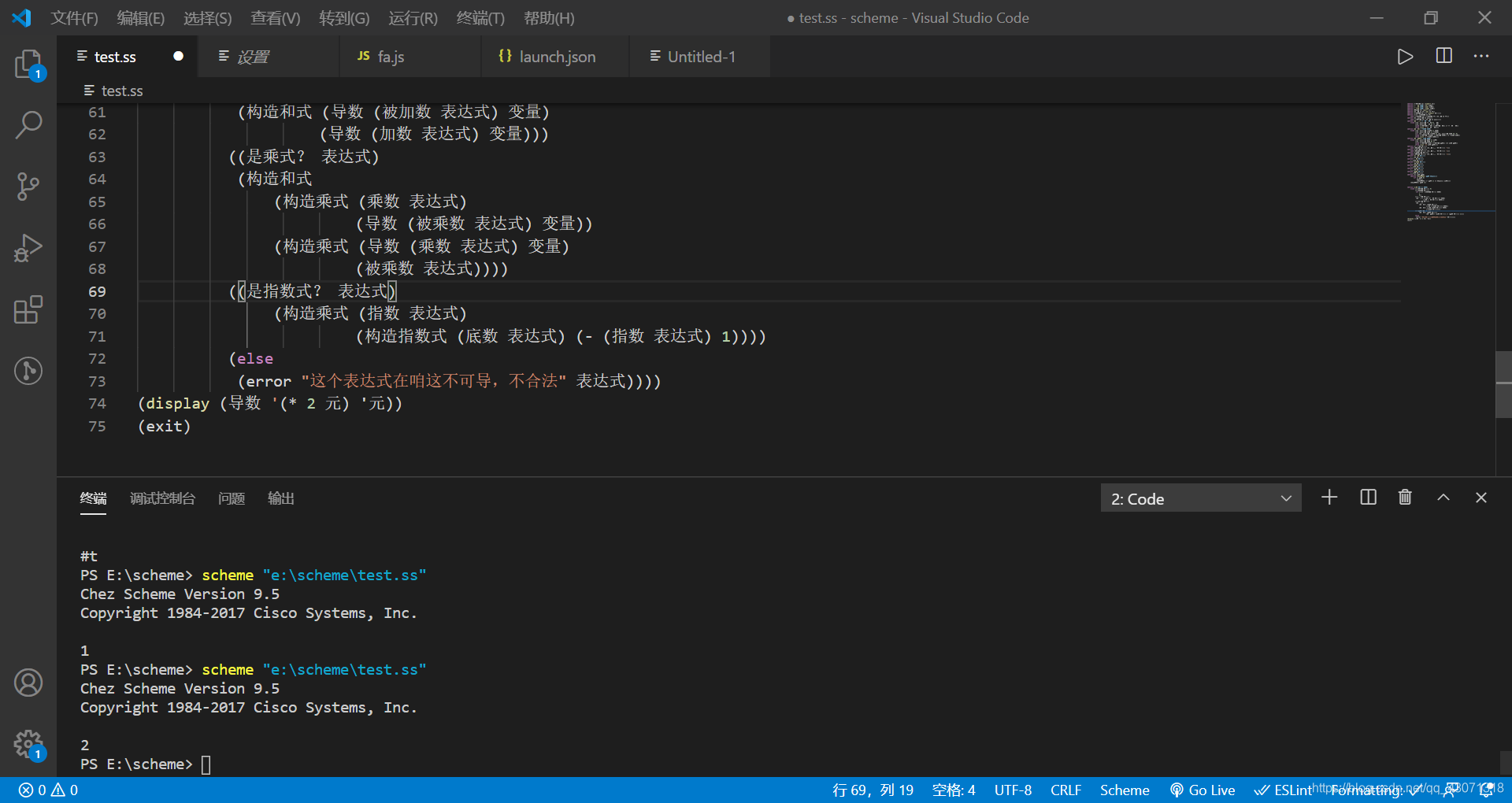
(display (导数 '(* 2 元) '元))
(exit)

练习2.57
请扩充求导程序，使之能处理任意项(两项或者更多项)的和与乘积。这样，上面的最后一个例子就可以表示为:

(deriv '(* x y (+ x 3)) 'x)

设法通过只修改和与乘积的表示，而完全不修改过程deriv的方式完成这一扩充。例如，让一个和式的addend是它的第一项，而其augend是和式中的其余项。

（未完待续。。。这节还有俩练习，回头再写吧，搂了一眼题目……嗯……还有答案，有点麻烦，以后再写吧）

3.实例：集合的表示

在前面的实例中，我们已经构造起两类复合数据对象的表示:有理数和代数表达式。在这两个实例中，我们都采用了某一种选择，在构造时或者选择成员时去简化(约简)有关的表示。除此之外，选择用表的形式来表示这些结构都是直截了当的。现在我们要转到集合的表示问题，此时，表示方式的选择就不那么显然了。实际上，在这里存在几种选择，而且它们相互之间在几个方面存在明显的不同。

非形式地说，一个集合就是一些不同对象的汇集。要给出一个更精确的定义，我们可以利用数据抽象的方法，也就是说，用一组可以作用于“集合”的操作来定义它们。这些操作是union-set，intersection-set, element-of-set?和adjoin-set。 其中element-of-set?是一个谓词，用于确定某个给定元素是不是某个给定集合的成员。adjoin-set以一个对象和一个集合为参数，返回一个集合，其中包含了原集合的所有元素，再加上刚刚加入进来的这个新元素。union-set计算出两个集合的并集，这也是一个集合，其中包含了所有属于两个参数集合之一的元素。intersection-set计算出两个集合的交集，它包含着同时出现在两个参数集合中的那些元素。从数据抽象的观点看，我们在设计有关的表示方面具有充分的自由，只要在这种表示上实现的上述操作能以某种方式符合上面给出的解释。

集合作为未排序的表

集合的一种表示方式是用其元素的表，其中任何元素的出现都不超过一次。这样，空集就用空表来表示。对于这种表示形式，element-of-set?类似于2.3.1节的过程memq，但它应该用equal?而不是eq?，以保证集合元素可以不是符号：

(define (element-of-set? x set)
    (cond ((null? set) false)
          ((equal? x (car set)) true)
          (else (element-of-set? x (cdr set)))))

尝试将上述过程直译为汉语：

（定义 （属于？ 元 集合）
    （情况符合 （（到空值了？ 集合） 不）
             （（相等？ 元 （前头的项 集合）） 是）
             （否则 （属于？ 元 （后面的项 集合）））））

利用它就能写出adjoin-set.如果要加人的对象已经在相应集合里，那么就返回那个集合；否则就用cons将这一对象加入表示集合的表里：

(define (adjoin-set x set)
    (if (element-of-set? x set)
        set
        (cons x set)))

尝试将上述过程直译为汉语：

（定义 （添加 元 集合）
    （如果 （属于？ 元 集合）
           集合
           （序对 元 集合）））

实现intersection-set时可以采用递归策略:如果我们已知如何做出set2与set1的cdr
的交集，那么就只需要确定是否应将set1的car包含到结果之中了，而这依赖于(car set1)是否也在set2里。下面是这样写 出的过程：

(define (intersection-set set1 set2)
    (cond ((or (null? set1) (null? set2)) '())
          ((element-of-set? (car set1) set2)
           (cons (car set1)
                 (intersection-set (cdr set1) set2)))
          (else (intersection-set (cdr set1) set2))))

尝试把上述过程直译为汉语：

（定义 （交集 集合甲 集合乙）
     （情况符合 （（或 （为空？ 集合甲）（为空？ 集合乙））‘（））
              （（属于？（前项 集合甲） 集合乙）
                （序对 （前项 集合甲）
                      （交集 （后面的项 集合甲） 集合乙）））
              （否则 （交集 （后面的项 集合甲） 集合乙））））

在设计一种表示形式时，有一件必须关注的事情是效率问题。为考虑这一问题，就需要考虑上面定义的各集合操作所需要的工作步数。因为它们都使用了element-of-set，这一操作的速度对整个集合的实现效率将有重大影响。在上面这个实现里，为了检查某个对象是否为一个集合的成员，element-of-set? 可能不得不扫描整个集合(最坏情况是这一元素恰好不在集合里)。因此，如果集合有n个元素，element-of - set?就可能需要n步才能完成。这样，这一操作所需的步数将以$\Theta (n)$的速度增长。adjoin-set使用了这个操作，因此它所需的步数也以$\Theta (n)$的速度增长。而对于intersection-set，它需要对set1的每个元素做一次element-of -set?检查，因此所需步数将按所涉及的两个集合的大小之乘积增长，或者说，在两个集合大小都为n时就是$\Theta (n^2)$。union-set 的情况也是如此。

练习2.59
请为采用未排序表的集合实现定义union-set操作。

解：

(define (union-set set1 set2)
    (cond ((or (null? set1) (null? set2)) '())
          ((not (element-of-set? (car set1) set2))
           (cons (car set1)
                 (union-set (cdr set1) set2)))
          (else (union-set (cdr set1) set2))))

尝试把上述过程直译为汉语：

（定义 （并集 集合甲 集合乙）
    （情况符合 （（或 （为空？ 集合甲）（为空？ 集合乙）） ‘（））
             （（不 （属于？ （前项 集合甲） 集合乙））
               （序对 （前项 集合甲）
                     （并集 （后面的项 集合甲） 集合乙）））
             （其它情况 （并集 （后面的项 集合甲） 集合乙））））

练习2.60
我们前面说明了如何将集合表示为没有重复元素的表。现在假定允许重复，例如，集合{1,2,3}可能被表示为表(2321322)。请为在这种表示上的操作设计过程element-of -set?. adjoin-set、 union-set 和intersection-set。与前面不重复表示里的相应操作相比，现在各个操作的效率怎么样?在什么样的应用中你更倾向于使用这种表示，而不是前面那种无重复的表示？

（以后会写的，这题不难）

集合作为排序的表

加速集合操作的一-种方式是改变表示方式，使集合元素在表中按照上升序排列。为此，我们就需要有某种方式来比较两个元素，以便确定哪个元素更大一些。 例如，我们可以按字典序做符号的比较，或者同意采用某种方式为每个对象关联一个唯一的数，在比较元素的时候就比较与之对应的数。为了简化这里的讨论，我们将仅仅考虑集合元素是数值的情况，这样就可以用>和<做元素的比较了。下面将数的集合表示为元素按照上升顺序排列的表。在前面第一种表示方式下，集合{1, 3, 6, 10}的元素在相应的表里可以任意排列，而在现在的新表示方式中，我们就只允许用表(1 3 6 10)。

从操作element-of-set?可以看到采用有序表示的一个优势：为了检查一个项的存在性，现在就不必扫描整个表了。如果检查中遇到的某个元素大于当时要找的东西，那么就可以断定这个东西根本不在表里：

(define (element-of-set? x set)
    (cond ((null? set) false)
          ((= x (car set)) true)
          ((< x (car set)) false)
          (else (element-of-set? x (cdr set)))))

尝试把上述过程直译为汉语：

（定义 （属于？ 元 集合）
    （情况符合 （（为空值？ 集合） 否）
             （（= 元 （前项 集合）） 是）
             （（< 元 （前项 集合）） 否）
             （其它情况 （属于？ 元 （后面的项 集合）））））

这样能节约多少步数呢?在最坏情况下，我们要找的项目可能是集合中的最大元素，此时所需步数与采用未排序的表示时一样。但在另一方面，如果需要查找许多不同大小的项，我们总可以期望，有些时候这一检索可以在接近表开始处的某一点停止，也有些时候需要检查表的一大部分。平均而言，我们可以期望需要检查表中的一半元素，这样，平均所需的步数就是大约n/2。这仍然是θ(n)的增长速度，但与前一实现相比，平均来说，现在我们节约了大约一半的步数(这一解释并不合理，因为前面说未排序表需要检查整个表，考虑的只是–种特殊情况：查找没有出现在表里的元素。如果查找的是表里存在的元素，即使采用未排序的表，平均查找长度也是表元素的一半。- -译者注)。（前面裘宗燕老师的注解牛逼啊！- -我注）

操作intersection-set的加速情况更使人印象深刻。在未排序的表示方式里，这一操作需要$\Theta (n^2)$的步数，因为对set1的每个元素，我们都需要对set2做一次完全的扫描。 对于排序表示则可以有一种更聪明的方法。我们在开始时比较两个集合的起始元素，例如x1和x2。如果x1等于x2，那么这样就得到了交集的一个元素，而交集的其他元素就是这两个集合的cdr的交集。如果此时的情况是x1小于x2，由于x2是集合set2的最小元素，我们立即可以断定x1不会出现在集合set2里的任何地方，因此它不应该在交集里。这样，两集合的交集就等于集合set2与set1的cdr的交集。与此类似，如果x2小于x1，那么两集合的交集就等于集合set1与set2的cdr的交集。下面是按这种方式写出的过程：

(define (intersection-set set1 set2)
    (if (or (null? set1) (null? set2))
        '()
        (let ((x1 (car set1)) ((x2 (car set2)))
          (cond ((= x1 x2)
                 (cons x1
                       (intersection-set (cdr set1)
                                         (cdr set2))))
                ((< x1 x2)
                 (intersection-set (cdr set1) set2))
                ((< x2 x1)
                 (intersection-set set1 (cdr set2))))))))

尝试将上述过程直译为汉语：

（定义 （交集 集合甲 集合乙）
    （如果 （或 （为空？ 集合甲）（为空？ 集合乙））
           ‘（）
          （命 （（甲首 （前头的项 集合甲）） （（乙首 （前头的项 集合乙）））
              （情况符合 （（= 甲首 乙首）
                         （序对 甲首
                              （交集 （后面的项 集合甲）
                                    （后面的项 集合乙））））
                        （（< 甲首 乙首）
                          （交集 （后面的项 集合甲）集合乙））
                        （（< 乙首 甲首）
                          （交集 甲首 （后面的项 集合乙））））））））

为了估计出这一过程所需的步数，请注意，在每个步骤中，我们都将求交集问题归结到更小集合的交集计算问题——去掉了set1和set2之一或者是两者的第一个元素。这样，所需步数至多等于set1与set2的大小之和，而不像在未排序表示中它们的乘积。这也就是$\Theta (n)$的增长速度，而不是$\Theta (n^2)$——这一加速非常明显，即使对中等大小的集合也是如此。

练习2.61
请给出采用排序表示时adjoin-set的实现。通过类似element-of-set?的方式说明，可以如何利用排序的优势得到一个过程，其平均所需的步数是采用未排序表示时的一半。

解：

(define (adjoin-set x set)
    (cond ((null? set) (list x))
          ((< (car set) x) (cons (car set) (adjoin-set x (cdr set))))
          ((= (car set) x) set)
          (else (cons x set))))

尝试将上述过程直译为汉语：

（定义 （添加 元 集合）
    （情况符合 （（为空？ 集合）（序列 元））
             （（< （前头的项 集合） 元）（序对 （前头的项 集合）（添加 元 （后面的项 集合））））
             （（= （前头的项 集合）元）集合）
             （其它情况 （序对 元 集合））））

如果是排好的序，最好的情况是刚排查到第一个元素就找到了元素是否该被添加以及该被添加在的位置，最坏的情况才是要排查到最后一个元素才知道，新来的元素大小是随机的，因此平均只需查找半程的集合，而对于为排序的集合，每次都需要排查整个集合，因此排序过的集合执行添加元素平均所需步数比未排序的少一半。

练习2.62
请给出在集合的排序表示上union-set的一个$\Theta (n)$实现。

解：

(define (union-set set1 set2)
    (cond ((null? set1) set2)
          ((null? set2) set1)
          (else
    		(let ((x1 (car set1)) (x2 (car set2)))
      			  (cond ((= x1 x2)
             			 (cons x1
                   			   (union-set (cdr set1)(cdr set2))))
            			((< x1 x2)
             			 (cons x1 
                   			   (union-set (cdr set1) set2)))
            			((> x1 x2)
             			 (cons x2
                   		 	   (union-set set1 (cdr set2)))))))))

尝试将上述过程直译为汉语：

（定义 （并集 集合甲 集合乙）
    （情况符合 （（为空？ 集合甲） 集合乙）
             （（为空？ 集合乙） 集合甲）
             （其它情况
    			（命 （（甲首 （前头的项 集合甲））（乙首 （前头的项 集合乙）））
        			  （情况符合 （（= 甲首 乙首）
                   				 （序对 甲首 （并集 （后面的项 集合甲）（后面的项 集合乙））））
                 				（（< 甲首 乙首）
                   				  （序对 甲首 （并集 （后面的项 集合甲）集合乙）））
                 				（（> 甲首 乙首）
                   				  （序对 乙首 （并集  集合甲 （后面的项 集合乙）））））））））

集合作为二叉树

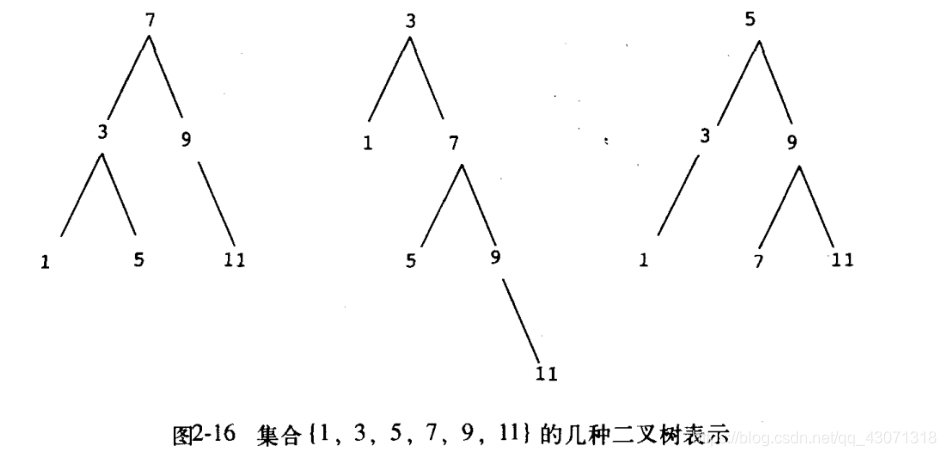
如果将集合元素安排成一棵树的形式，我们还可以得到比排序表表示更好的结果。树中每个结点保存集合中的一个元素，称为该结点的“数据项”，它还链接到另外的两个结点(可能为空)。其中“左边”的链接所指向的所有元素均小于本结点的元素，而“右边”链接到的元素都大于本结点里的元素。图2-16显示的是一棵表示集合的树。同一个集合表示为树可以有多种不同的方式，我们对一个合法表示的要求就是，位于左子树里的所有元素都小于本结点里的数据项，而位于右子树里的所有元素都大于它。

（注：这里也就是要把集合表示为平衡二叉树）

树表示方法的优点在于：假定我们希望检查某个数x是否在一个集合里，那么就可以用x与树顶结点的数据项相比较。如果x小于它，我们就知道现在只需要搜索左子树；如果x比较大，那么就只需搜索右子树。在这样做时，如果该树是“平衡的”， 也就是说，每棵子树大约是整个树的一半大， 那么，这样经过一步，我们就将需要搜索规模为n的树的问题，归约为搜索规模为n/2的树的问题。由于经过每个步骤能够使树的大小减小一半，我们可以期望搜索规模为n的树的计算步数以θ(log n)速度增长。在集合很大时，相对于原来的表示，现在的操作速度将明显快得多。

我们可以用表来表示树，将结点表示为三个元素的表：本结点中的数据项，其左子树和右子树。以空表作为左子树或者右子树，就表示没有子树连接在那里。我们可以用下面过程描述这种表示：

(define (entry tree) (car tree))
(define (left-branch tree) (cadr tree))
(define (right-branch tree) (caddr tree))
(define (make-tree entry left right)
    (list entry left right))

尝试将上述过程直译为汉语：

（定义 （根 树）（第一项 树））
（定义 （左分支 树）（第二项 树））
（定义 （右分支 树）（第三项 树））
（定义 （构建树 根 左 右）
    （序列 根 左 右））

现在，我们就可以采用上面描述的方式实现过程element-of-set?了：

(define (element-of-set? x set)
    (cond ((null? set) false)
          ((= x (entry set)) true)
          ((< x (entry set))
           (element-of-set? x (left-branch set)))
          ((> x (entry set))
           (element-of-set? x (right-branch set)))))

尝试将上述过程直译为汉语：

（定义 （属于？ 元 集合树）
    （情况符合 （（到空值了？ 集合树）不）
             （（= 元 （根 集合树））是）
             （（< 元 （根 集合树））
               （属于？ 元 （左分支 集合树）））
             （（> 元 （根 集合树））
               （属于？ 元 （右分支 集合树）））））

向集合里加入一个项的实现方式与此类似，也需要θ(log n)步数。为了加入元素x，我们需要将x与结点数据项比较，以便确定x应该加入右子树还是左子树中。在将x加入适当的分支之后，我们将新构造出的这个分支、原来的数据项与另一分支放到一起。如果x等于这个数据项，那么就直接返回这个结点。如果需要将x加入一个空子树，那么我们就生成一棵树，以x作为数据项，并让它具有空的左右分支。

添加一个元素到树中的子过程拆分出来差不多这三种情况：

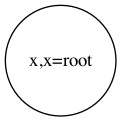
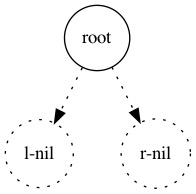
新元素在现有树中，就不用添加了，直接把现有树返回：

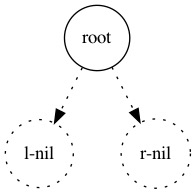
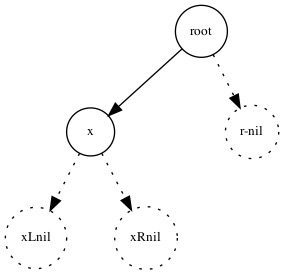
下面是这个过程：

(define (adjoin-set x set)
    (cond ((null? set) (make-tree x '() '()))
          ((= x (entry set)) set)
          ((< x (entry set))
           (make-tree (entry set)
                      (adjoin-set x (left-branch set))
                      (right-branch set)))
          ((> x (entry set))
           (make-tree (entry set)
                      (left-branch set)
                      (adjoin-set x (right-branch set))))))

尝试把上述过程直译为汉语：

（定义 （添加 元 集合树）
    （情况符合 （（为空值？ 集合树）（构建树 元 ‘（） ’（）））
             （（= 元 （根 集合树）） 集合树）
             （（< 元 （根 集合树））
               （构建树 （根 集合树）
                       （添加 元 （左分支 集合树））
                       （右分支 集合树）））
             （（> 元 （根 集合树））
               （构建树 （根 集合树）
                       （左分支 集合树）
                       （添加 元 （右分支 集合树））））））

我们在上面断言，搜索树的操作可以在对数步数中完成，这实际上依赖于树“平衡”的假设，也就是说，每个树的左右子树中的结点大致上一样多，因此每棵子树中包含的结点大约就是其父的一半。但是我们怎么才能确保构造出的树是平衡的呢？即使是从一棵平衡的树开始工作，采用adjoin-set加入元素也可能产生出不平衡的结果。因为新加入元素的位置依赖于它与当时已经在树中的那些项比较的情况。我们可以期望，如果“随机地”将元素加入树中，平均而言将会使树趋于平衡。但在这里并没有任何保证。例如，如果我们从空集出发，顺序将数值1至7加入其中，我们就会得到如图2-17所示的高度不平衡的树。在这个树里，所有的左子树都为空，所以它与简单排序表相比一点优势也没有。

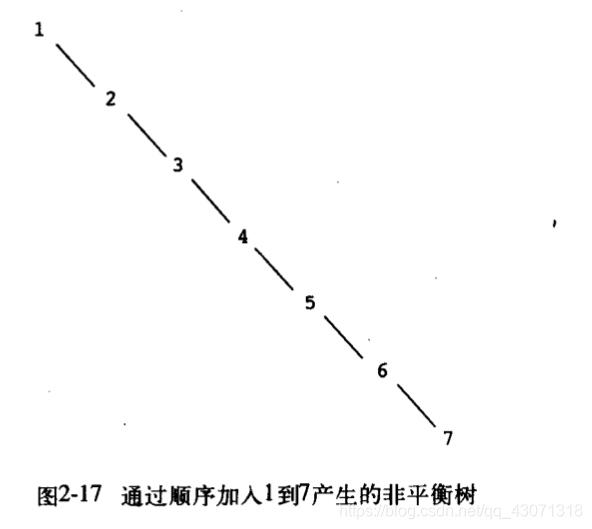
解决这个问题的一种方式是定义一个操作，它可以将任意的树变换为一棵具有同样元素的平衡树。在每执行过几次adjoin-set操作之后，我们就可以通过执行它来保持树的平衡。当然，解决这一问题的方法还有许多，大部分这类方法都涉及到设计一种新的数据结构，设法使这种数据结构上的搜索和插入操作都能够在θ(log n)步数内完成。

注：这种结构的例子如B树和红黑树。

练习2.63
下面两个过程都能将树变换为表：

(define (tree->list-1 tree)
    (if (null? tree)
        '()
        (append (tree->list1 (left-branch tree))
                (cons (entry tree)
                      (tree->list-1 (right-branch tree))))))
(define (tree->list-2 tree)
    (define (copy-to-list tree result-list)
        (if (null? tree)
            result-list
            (copy-to-list (left-branch tree)
                          (cons (entry tree)
                                (copy-to-list (right-branch tree)
                                              result-list))))))

（定义 （中序序列 树）
    （如果 （为空？ 树）
           ‘（）
           （合并 （中序序列 （左分支 树））
                 （序对 （根 树）
                       （中序序列 （右分支 树））））））
（定义 （中序序列 树）
    （定义 （拷贝至序列 树 结果序列）
        （如果 （到空值了？ 树）
               结果序列
              （拷贝至序列 （左分支 树）
                         （序对 （根 树）
                               （拷贝至序列 （右分支 树）
                                           结果序列））））））

a)这两个过程对所有的树都产生同样结果吗？如果不是，它们产生出的结果有什么不同？它们对图2-16中的那些树产生什么样的表？
b)将n个结点的平衡树变换为表时，这两个过程所需的步数具有同样量级的增长速度吗？如果不一样，哪个过程增长得慢一些？

解：
a) 都是同样的结果，返回的是“根，左，右”这样的中序序列，就是根会在中间。
b) 不一样，第一种的append过程会把复杂度提高n倍。

练习2.64
下面过程list->tree将一个有序表变换为一棵平衡二叉树。其中的辅助函数partial-tree以整数n和一个至少包含n个元素的表为参数，构造出一棵包含这个表的前n个元素的平衡树。由partial-tree返回的结果是一个序对(用cons构造)， 其car是构造出的树，其cdr是没有包含在树中那些元素的表。

(define (list->tree elements)
    (car (partial-tree elements (length elements))))
(define (partial-tree elts n)
    (if (= n 0)
        (cons '() elts)
        (let ((left-size (quotient (- n 1) 2)))
          (let ((left-result (partial-tree elts left-size)))
            (let ((left-tree (car left-result))
                  (non-left-elts (cdr left-result))
                  (right-size (- n (+ left-size 1))))
               (let ((this-entry (car non-left-elts))
                     (right-result (partial-tree (cdr non-left-elts)
                                   right-size)))
                  (let ((right-tree (car right-result))
                        (remaining-elts (cdr right-result)))
                    (cons (make-tree this-entry left-tree right-tree)
                          remaining-elts))))))))

尝试将上述过程直译为汉语：

（定义 （序列转为树 序列元素）
    （前项 （提取树 序列元素 （个数 序列元素））））
（定义 （提取树 所有元素 树大小）
    （如果 （= 树大小 0）
          （序对 ‘（） 所有元素）
          （命 （（左子树大小 （商 （- 树大小 1）2）））
            （命 （（提取左子树 （提取树 所有元素 左子树大小）））
              （命 （（左子树 （前项 提取左子树））
                    （非左子树元素 （后项 提取左子树））
                    （右子树大小 （- 树大小 （+ 左子树大小 1））））
                  （命 （（树根 （前项 非左子树元素））
                        （提取右子树 （提取树 （后面的项 非左子树元素）右子树大小）））
                      （命 （（右子树 （前项 提取右子树））
                            （剩余元素 （后面的项 提取右子树）））
                          （序对 （构建树 树根 左子树 右子树）
                                 剩余元素））））））））

a)请简要地并尽可能清楚地解释为什么partial-tree能完成工作。请画出将list->tree用于表(1 3 5 7 9 11)产生出的树。
b)过程list->tree转换n个元素的表所需的步数以什么量级增长?

解：
a)
对于一个 list，首先计算出构造左子树和右子树需要的结点数，然后用所需结点递归地调用 partial-tree 构造子树，最后用生成的子树和根结点构造树。list->tree 用于表 (1 3 5 7 9 11) 产生出的树为：

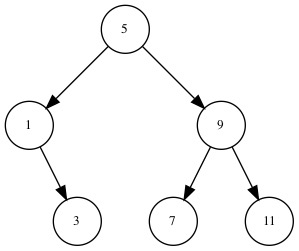
b)
partial-tree正好会把每个元素访问一遍，因此所需步数以$\Theta (n)$增长。

练习2.65
利用练习2.63和练习2.64的结果，给出对采用(平衡)二叉树方式实现的集合的union-set和intersection-set操作的$\Theta (n)$实现。

解：
首先，我得说，写这道题的时候我在想，scheme语言要如何应对多态的需求呢？能不能有一个union-set函数，对于传入的无论是树结构还是一般的表结构都能正确地给出结果呢？我现在还没有答案。

仅在这个题的情景下，我还是决定把这题要求的union-set和intersection-set命名为union-tree和intersection-tree吧，我觉得这样更可以明确其需要传入的数据结构以及返回的数据结构：

(define (make-tree entry left right)
    (list entry left right))
(define (left-branch tree)
    (cadr tree))
(define (right-branch tree)
    (caddr tree))
(define (entry tree)
    (car tree))
(define (intersection-set set1 set2)
   (if (or (null? set1) (null? set2)) 
       '()
       (let ((x1 (car set1)) (x2 (car set2)))
         (cond ((= x1 x2)
                (cons x1
                      (intersection-set (cdr set1)
                                        (cdr set2))))
               ((< x1 x2)
                (intersection-set (cdr set1) set2))
               ((> x1 x2)
                (intersection-set set1 (cdr set2)))))))
(define (union-set set1 set2)
    (cond ((null? set1) set2)
          ((null? set2) set1)
          (else 
               (let ((x1 (car set1)) (x2 (car set2)))
                (cond ((= x1 x2)
                        (cons x1
                              (union-set (cdr set1)(cdr set2))))
                      ((< x1 x2)
                        (cons x1
                              (union-set (cdr set1) set2)))
                      ((> x1 x2)
                        (cons x2
                              (union-set set1 (cdr set2)))))))))
(define (tree->list tree)
    (define (copy-to-list tree result-list)
        (if (null? tree)
            result-list
            (copy-to-list (left-branch tree)
                          (cons (entry tree)
                                (copy-to-list (right-branch tree)
                                              result-list)))))
    (copy-to-list tree '()))
(define (list->tree elements)
    (car (partial-tree elements (length elements))))
(define (partial-tree elts n)
    (if (= n 0)
        (cons '() elts)
        (let ((left-size (quotient (- n 1) 2)))
          (let ((left-result (partial-tree elts left-size)))
            (let ((left-tree (car left-result))
                  (non-left-elts (cdr left-result))
                  (right-size (- n (+ left-size 1))))
               (let ((this-entry (car non-left-elts))
                     (right-result (partial-tree (cdr non-left-elts)
                                   right-size)))
                  (let ((right-tree (car right-result))
                        (remaining-elts (cdr right-result)))
                    (cons (make-tree this-entry left-tree right-tree)
                          remaining-elts))))))))
(define (union-tree tree1 tree2)
    (list->tree (union-set (tree->list tree1) (tree->list tree2))))
(define (intersection-tree tree1 tree2)
    (list->tree (intersection-set (tree->list tree1) (tree->list tree2))))
(define tree1 (list->tree '(1 2 3 5 6 8 10 11)))
(define tree2 (list->tree '(2 4 6 8 11 13)))
(display (tree->list (union-tree tree1 tree2)))
(newline)
(display (tree->list (intersection-tree tree1 tree2)))
(exit)

那对于这题，我觉得我又可以开开心心地给出其中文命名的版本啦：

(define (第一项 序列) (car 序列))
(define (第二项 序列) (cadr 序列))
(define (第三项 序列) (caddr 序列))
(define (前项 序对) (car 序对))
(define (后项 序对) (cdr 序对))
(define (序对 前项 后项) (cons 前项 后项))
(define (个数 序列元素) (length 序列元素))
(define (长度 序列) (length 序列))
(define (元素个数 序列) (length 序列))
(define (前头的项 序列) (car 序列))
(define (后面的项 序列) (cdr 序列))
(define (到空值了？ 序列) (null? 序列))
(define (为空？ 序列) (null? 序列))
(define (商 被除数 除数) (quotient 被除数 除数))
(define (输出 内容) (display 内容))
(define (显示 内容) (display 内容))
(define (换行) (newline))
(define (退出) (exit))
(define (构建树 根 左子树 右子树)
    (list 根 左子树 右子树))
(define (左子树 树)
    (第二项 树))
(define (右子树 树)
    (第三项 树))
(define (根 树)
    (第一项 树))
(define (升序序列交集 集合甲 集合乙)
   (if (or (为空？ 集合甲) (为空？ 集合乙)) 
       '()
       (let ((甲首 (前头的项 集合甲)) (乙首 (前头的项 集合乙)))
         (cond ((= 甲首 乙首)
                (序对 甲首
                      (升序序列交集 (后面的项 集合甲)
                                   (后面的项 集合乙))))
               ((< 甲首 乙首)
                (升序序列交集 (后面的项 集合甲) 集合乙))
               ((> 甲首 乙首)
                (升序序列交集 集合甲 (后面的项 集合乙)))))))

(define (升序序列并集 集合甲 集合乙)
    (cond ((为空？ 集合甲) 集合乙)
          ((为空？ 集合乙) 集合甲)
          (else 
               (let ((甲首 (前头的项 集合甲)) (乙首 (前头的项 集合乙)))
                (cond ((= 甲首 乙首)
                       (序对 甲首
                             (升序序列并集 (后面的项 集合甲)(后面的项 集合乙))))
                      ((< 甲首 乙首)
                       (序对 甲首
                             (升序序列并集 (后面的项 集合甲) 集合乙)))
                      ((> 甲首 乙首)
                       (序对 乙首
                             (升序序列并集 集合甲 (后面的项 集合乙)))))))))
(define (树对应的中序序列 树)
    (define (中序遍历 树 结果序列)
        (if (到空值了？ 树)
            结果序列
            (中序遍历 (左子树 树)
                     (序对 (根 树)
                           (中序遍历 (右子树 树)
                                    结果序列)))))
    (中序遍历 树 '()))
(define (中序序列对应的树 序列元素)
    (前项 (树和剩余元素 序列元素 (个数 序列元素))))
(define (树和剩余元素 所有元素 树大小)
    (if (= 树大小 0)
        (序对 '() 所有元素)
        (let ((左子树大小 (商 (- 树大小 1) 2)))
          (let ((左子树和剩余元素 (树和剩余元素 所有元素 左子树大小)))
            (let ((左子树 (前项 左子树和剩余元素))
                  (非左子树元素 (后项 左子树和剩余元素))
                  (右子树大小 (- 树大小 (+ 左子树大小 1))))
              (let ((根 (前头的项 非左子树元素))
                    (右子树和剩余元素 (树和剩余元素 (后面的项 非左子树元素) 右子树大小)))
                (let ((右子树 (前项 右子树和剩余元素))
                      (剩余元素 (后项 右子树和剩余元素)))
                  (序对 (构建树 根 左子树 右子树) 剩余元素))))))))
(define (树的交集 树甲 树乙)
    (中序序列对应的树 (升序序列交集 (树对应的中序序列 树甲) (树对应的中序序列 树乙))))
(define (树的并集 树甲 树乙)
    (中序序列对应的树 (升序序列并集 (树对应的中序序列 树甲) (树对应的中序序列 树乙))))
(define 树甲 (中序序列对应的树 '(1 2 3 5 6 8 10 11)))
(define 树乙 (中序序列对应的树 '(2 4 6 8 11 13)))
(输出 (树对应的中序序列 (树的交集 树甲 树乙)))
(换行)
(输出 (树对应的中序序列 (树的并集 树甲 树乙)))

(退出)

集合与信息检索

我们考察了用表表示集合的各种选择，并看到了数据对象表示的选择可能如何深刻地影响到使用数据的程序的性能。关注集合的另一个原因是，这里所讨论的技术在涉及信息检索的各种应用中将会一次又一次地出现。

现在考虑一个包含大量独立记录的数据库，例如一个企业中的人事文件，或者一个会计系统里的交易记录。典型的数据管理系统都需将大量时间用在访问和修改所存的数据上，因此就需要访问记录的高效方法。完成此事的一种方式是将每个记录中的一部分当作标识key(键值)。所用键值可以是任何能唯一标识记录的东西。对于人事文件而言，它可能是雇员的ID编码。对于会计系统而言，它可能是交易的编号。在确定了采用什么键值之后，就可以将记录定义为一种数据结构，并包含key选择过程，它可以从给定记录中提取出有关的键值。

现在就可以将这个数据库表示为一个记录的集合。为了根据给定键值确定相关记录的位
置，我们用一个过程lookup，它以一个键值和一个数据库为参数，返回具有这个键值的记录，或者在找不到相应记录时报告失败。lookup的实现方式几乎与element-of-set?一模一样，如果记录的集合被表示为未排序的表，我们就可以用：

(define (lookup given-key set-of-records)
    (cond ((null? set-of-records) false)
          ((equal? given-key (key (car set-of-records)))
           (car set-of-records))
          (else (lookup given-key (cdr set-of-records)))))

尝试把上述过程直译为汉语：

（定义 （根据所给键值寻找 所给键值 数据记录）
    （情况符合 （（为空？ 数据记录） 无）
             （（等于？ 所给键值 （键 （前头的项 数据记录）））
               （前头的项 数据记录））
             （其它情况 （根据所给键值寻找 所给键值 （后面的项 数据记录）））））

不言而喻，还有比未排序表更好的表示大集合的方法。常常需要“随机访问”其中记录的信息检索系统通常用某种基于树的方法实现，例如用前面讨论过的二叉树。在设计这种系统时，数据抽象的方法学将很有帮助。设计师可以创建某种简单而直接的初始实现，例如采用未排序的表。对于最终系统而言，这种做法显然并不合适，但采用这种方式提供一个“一挥而就”的数据库，对用于测试系统的其他部分则可能很有帮助。然后可以将数据表示修改得更加精细。如果对数据库的访问都是基于抽象的选择函数和构造函数，这种表示的改变就不会要求对系统其余部分做任何修改。

练习2.66
假设记录的集合采用二叉树实现，按照其中作为键值的数值排序。请实现相应的lookup过程。

解：

(define (lookup given-key set-of-records)
    (cond ((null? set-of-records) false)
          ((equal? given-key (key (entry set-of-records))) (entry set-of-records))
          ((< given-key (key (entry set-of-records)))
           (lookup given-key (left-branch set-of-records)))
          ((> given-key (key (entry set-of-records)))
           (lookup given-key (right-branch set-of-records)))))

尝试将上述过程直译为汉语：

（定义 （找寻 所给键值 数据记录）
    （情况符合 （（到空值了？ 数据记录）无）
             （（等于？ 所给键值 （键 （根 数据记录））） （根 数据记录））
             （（< 所给键值 （键 （根 数据记录）））
               （找寻 所给键值 （左子树 数据记录）））
             （（> 所给键值 （键 （根 数据记录）））
               （找寻 所给键值 （右子树 数据记录）））））

4.实例：Huffman编码树

本节将给出一个实际使用表结构和数据抽象去操作集合与树的例子。这一应用是想确定一些用0和1 (二进制位) 的序列表示数据的方法。举例说，用于在计算机里表示文本的ASCII标准编码将每个字符表示为一个包含7个二进制位的序列，采用7个二进制位能够区分$2^7$种不同情况，即128个可能不同的字符。一般而言，如果我们需要区分n个不同字符，那么就需要为每个字符使用$lo{g}_2(n)$个二进制位。假设我们的所有信息都是用A、B、C、D、E、F、G和H这样8个字符构成的，那么就可以选择每个字符用3个二进制位，例如：

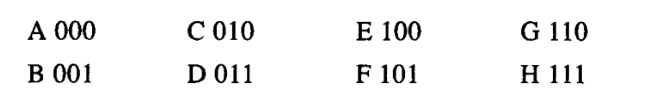
采用这种编码方式，消息：

BACADAEAFABBAAAGAH

将编码为54个二进制位

001000010000011000100000101000001001000000000110000111

像ASCII码和上面A到H编码这样的编码方式称为定长编码，因为它们采用同样数目的二进制位表示消息中的每一个字符。变长编码方式就是用不同数目的二进制位表示不同的字符，这种方式有时也可能有些优势。举例说，莫尔斯电报码对于字母表中各个字母就没有采用同样数目的点和划，特别是最常见的字母E只用一个点表示。一般而言，如果在我们的消息里，某些符号出现得很频繁，而另一些却很少见，那么如果为这些频繁出现的字符指定较短的码字，我们就可能更有效地完成数据的编码(对于同样消息使用更少的二进制位)。请考虑下面对于字母A到H的另一种编码：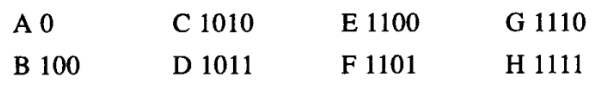
采用这种编码方式，上面的同样信息将编码为如下的串：

100010100101101100011010100100000111001111

这个串中只包含42个二进制位，也就是说，与上面定长编码相比，现在的这种方式节约了超过20%的空间。

采用变长编码有一个困难，那就是在读0/1序列的过程中确定何时到达了一个字符的结束。莫尔斯码解决这一问题的方式是在每个字母的点划序列之后用一个特殊的分隔符(它用的是一个间歇)。另一种解决方式是以某种方式设计编码，使得其中每个字符的完整编码都不是另一字符编码的开始一段(或称前缀)。这样的编码称为前缀码。在上面例子里，A编码为0而B编码为100,没有其他字符的编码由0或者100开始。

一般而言，如果能够通过变长前缀码去利用被编码消息中符号出现的相对频度，那么就能明显地节约空间。完成这件事情的一种特定方式称Huffman编码，这个名称取自其发明人David Huffman 。一个Huffman编码可以表示为一棵二叉树，其中的树叶是被编码的符号。树中每个非叶结点代表一个集合， 其中包含了这一结点之下的所有树叶上的符号。除此之外，位于树叶的每个符号还被赋予一个权重(也就是它的相对频度)，非叶结点所包含的权重是位于它之下的所有叶结点的权重之和。这种权重在编码和解码中并不使用。下面将会看到，在构造树的过程中需要它们的帮助。

图2-18显示的是上面给出的A到H编码所对应的Huffman编码树，树叶上的权重表明，这棵树的设计所针对的消息是，字母A具有相对权重8，B具有相对权重3，其余字母的相对权重都是1。

给定了一棵Huffman树，要找出任一符号的编码，我们只需从树根开始向下运动，直到到达了保存着这一符号的树叶为止，在每次向左行时就给代码加上一个0，右行时加上一个1。在确定向哪一分支运动时，需要检查该分支是否包含着与这一符号对应的叶结点，或者其集合中包含着这个符号。举例说，从图2-18中树的根开始，到达D的叶结点的方式是走一个右分支，而后一个左分支，而后是右分支，而后又是右分支，因此其代码为1011。

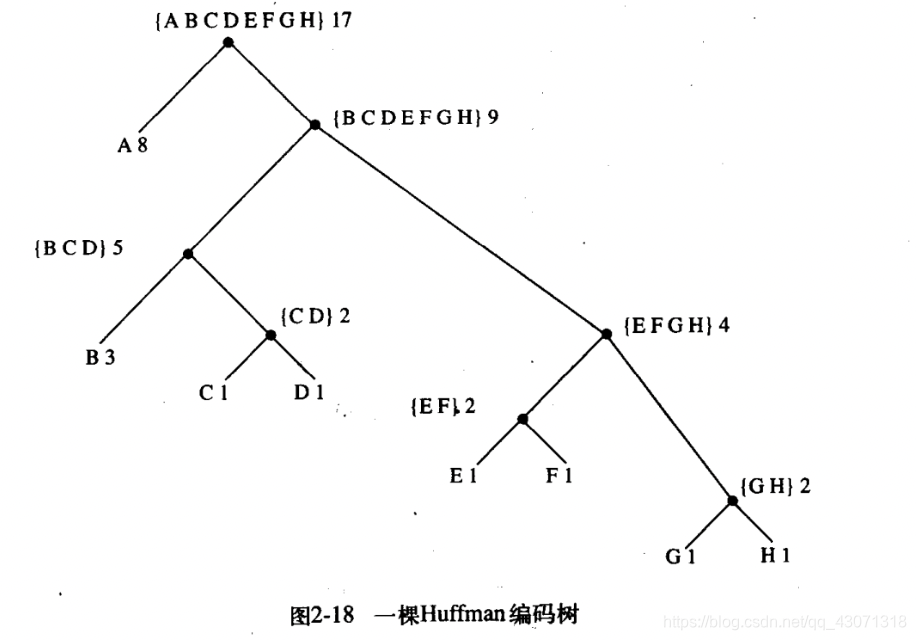
在用Huffman树做一个序列的解码时，我们也从树根开始，通过位序列中的0或1确定是移向左分支还是右分支。每当我们到达一个叶结点时，就生成出了消息中的一个符号。此时就重新从树根开始去确定下一个符号。例如，如果给我们的是上面的树和序列10001010.从树根开始，我们移向右分支（因为串中第一个位是1），而后向左分支(因为第二个位是0)，而后再向左分支(因为第三个位也是0)。这时已经到达B的叶，所以被解码消息中的第一个符号是B。现在再次从根开始，因为序列中下一个位是0，这就导致一次向左分支的移动，使我们到达A的叶。然后我们再次从根开始处理剩下的串1010，经过右左右左移动后到达了C。这样，整个消息也就是BAC。

生成Huffman树
给定了符号的“字母表”和它们的相对频度，我们怎么才能构造出“最好的”编码呢?换句话说，哪样的树能使消息编码的位数达到最少？Huffman给出了完成这件事的一个算法，并且证明了，对于符号所出现的相对频度与构造树的消息相符的消息而言，这样产生出的编码确实是最好的变长编码。我们并不打算在这里证明Huffman编码的最优性质，但将展示如何去构造Huffman树。

生成Huffman树的算法实际上十分简单，其想法就是设法安排这棵树，使得那些带有最低频度的符号出现在离树根最远的地方。这一构造过程从叶结点的集合开始，这种结点中包含各个符号和它们的频度，这就是开始构造编码的初始数据。现在要找出两个具有最低权重的叶，并归并它们，产生出一个以这两个结点为左右分支的结点。新结点的权重就是那两个结点的权重之和。现在我们从原来集合里删除前面的两个叶结点，并用这一新结点代替它们。随后继续这一过程，在其中的每一步都归并两个具有最小权重的结点，将它们从集合中删除，并用一个以这两个结点作为左右分支的新结点取而代之。当集合中只剩下一个结点时，这一过程终止，而这个结点就是树根。下面显示的是图2-18中的Huffman树的生成过程：

这一算法并不总能描述一棵唯一的树，这是因为，每步选择出的最小权重结点有可能不唯一。还有，在做归并时，两个结点的顺序也是任意的，也就是说，随便哪个都可以作为左分支或者右分支。

Huffman树的表示
在下面的练习中，我们将要做出一个使用Huffman树完成消息编码和解码，并能根据上面给出的梗概生成Huffman树的系统。开始还是讨论这种树的表示。

将一棵树的树叶表示为包含符号leaf、叶中符号和权重的表：

(define (make-leaf symbol weight)
    (list 'leaf symbol weight))

(define (leaf? object)
    (eq? (car object) 'leaf))

(define (symbol-leaf x) (cadr x))
(define (weight-eaf x) (caddr x))

尝试将上述过程直译为汉语：

（定义 （构造树叶 符号 权重）
    （序列 ‘叶 符号 权重））
（定义 （是树叶？ 结点）
    （同样？ （第一项 结点） ‘叶））
（定义 （叶上符号 树叶）（第二项 树叶））
（定义 （叶的权重 树叶）（第三项 树叶））

一棵一般的树也是一个表，其中包含-一个左分支、一个右分支、一个符号集合和一个权重。符号集合就是符号的表，这里没有用更复杂的集合表示。在归并两个结点做出一棵树时，树的权重也就是这两个结点的权重之和，其符号集就是两个结点的符号集的并集。因为这里的符号集用表来表示，通过2.2.1节的append过程就可以得到它们的并集：

(define (make-code-tree left right)
    (list left
          right
          (append (symbols left) (symbols right))
          (+ (weight left) (weight right))))

尝试将上述过程直译为汉语：

（定义 （构造编码树 左子树 右子树）
    （序列 左子树
          右子树
          （合并 （符号集合 左子树）（符号集合 右子树））
          （+ （权重 左子树）（权重 右子树））））

如果以这种方式构造，我们就需要采用下面的选择函数：

(define (left-branch tree) (car tree))

(define (right-branch tree) (cadr tree))

(define (symbols tree)
    (if (leaf? tree)
        (list (symbol-leaf tree))
        (caddr tree)))
        
(define (weight tree)
    (if (leaf? tree)
        (weight-leaf tree)
        (cadddr tree)))

（定义 （左子树 树）（第一项 树））
（定义 （左分支 树）（第一项 树））
（定义 （右子树 树）（第二项 树））
（定义 （右分支 树）（第二项 树））

（定义 （符号集合 树）
    （如果 （是树叶？ 树）
          （序列 （叶上符号 树））
          （第三项 树）））

（定义 （权重 树）
    （如果 （是树叶？ 树）
          （叶的权重 树）
          （第四项 树）））

在对树叶或者一般树调用过程symbols和weight时，它们需要做的事情有一点不同。这些不过是通用型过程(可以处理多于一种数据的过程)的简单实例，有关这方面的情况，在2.4节和2.5节将有很多讨论。

解码过程
下面的过程实现解码算法，它以一个0/1的表和一棵Huffman树为参数：

(define (decode bits tree)
    (define (decode-1 bits current-branch)
      (if (null? bits)
          '()
          (let ((next-branch
                 (choose-branch (car bits) current-branch)))
             (if (leaf? next-branch)
                 (cons (symbol-leaf next-branch)
                       (decode-1 (cdr bits) tree))
                 (decode-1 (cdr bits) next-branch)))))
     (decode-1 bits tree))
(define (choose-branch bit branch)
    (cond ((= bit 0) (left-branch branch))
          ((= bit 1) (right-branch branch))
          (else (error "bad bit -- CHOOSE-BRANCH" bit))))

尝试将上述过程直译为汉语：

（定义 （解码 编码序列 树）
    （定义 （执行解码 编码序列 当前分支）
       （如果 （到空值了？ 编码序列）
              ‘（）
              （命 （（下一分支 （选择分支 （前头的项 编码序列） 当前分支）））
                （如果 （是树叶？ 下一分支）
                      （序对 （叶上符号 下一分支）
                            （执行解码 （后面的项 编码序列） 树））
                      （执行解码 （后面的项 编码序列） 下一分支）））））
     （执行解码 编码序列 树））
     
（定义 （选择分支 码值 分支）
    （情况符合 （（= 码值 0）（左分支 分支））
              （（= 码值 1）（右分支 分支））
              （其它情况 （错误 “码值不合法 —— 选择分支” 码值））））

过程decode-1有两个参数，其中之一是包含二进制位的表，另一个是树中的当前位置。它不断在树里“向下”移动，根据表中下一个位是0或者1选择树的左分支或者右分支（这一工作由过程choose-branch完成)。一旦到达了叶结点，它就把位于这里的符号作为消息中的下一个符号，将其cons到对于消息里随后部分的解码结果之前。而后这一解码又从树根重新开始。请注意choose-branch里最后一个子句的错误检查，如果过程遇到了不是0/1的东西时就会报告错误。

带权重元素的集合
在树表示里，每个非叶结点包含着一个符号集合，在这里表示为一个简单的表。然而，上面讨论的树生成算法要求我们也能对树叶和树的集合工作，以便不断地归并一对一对的最小项。因为在这里需要反复去确定集合里的最小项，采用某种有序的集合表示会比较方便。

我们准备将树叶和树的集合表示为一批元素的表，按照权重的上升顺序排列表中的元素。下面用于构造集合的过程adjoin-set与练习2.61中描述的过程类似，但这里比较的是元素的权重,而且加入集合的新元素原来绝不会出现在这个集合里。

(define ((adjoin-set x set)
    (cond ((null? set) (list x))
              ((< (weight x) (weight (car set))) (cons x set))
              (else (cons (car set)
                                 (adjoin-set x (cdr set)))))))

尝试将上述过程直译为汉语：

（定义 （（添加 元素 集合）
    （情况符合 （（为空？ 集合）（序列 元素））
                       （（< （权重 元素）（权重 （前头的项 集合）））（序对 元素 集合））
                       （其它情况 （序对 （前头的项 集合）
                                                      （添加 元素 （后面的项 集合）））））））

下面过程以一个符号-权重对偶的表为参数，例如（(A 4) (B 2) (C 1) (D 1))，它构造出树叶的初始排序集合,以便Huffman算法能够去做归并：

(define (make-leaf-set pairs)
    (if (null? pairs)
        '()
        (let ((pair (car pairs)))
          (adjoin-set (make-leaf (car pair)
                                              (cadr pair))
                            (make-leaf-set (cdr pairs))))))

（定义 （构建树叶集合 符号-权重对偶表）
    （如果 （为空？ 符号-权重对偶表）
                  ‘（）
                  （命 （（符号-权重对偶 （前头的项 符号-权重对偶表）））
                      （添加 （构造树叶 （第一项 符号-权重对偶）
                                     （第二项 符号-权重对偶））
                             （构建树叶集合 （后面的项 符号-权重对偶表））））））

练习2.67
请定义一棵编码树和一个样例消息：

(define sample-tree
  (make-code-tree (make-leaf 'A 4)
                  (make-code-tree
                    (make-leaf 'B 2)
                    (make-code-tree (make-leaf 'D 1)
                                    (make-leaf 'C 1)))))
(define sample-message '(0 1 1 0 0 1 0 1 0 1 1 1 0))

尝试将上述过程直译为汉语：

（定义 样例树
  （构建编码树 （构造树叶 ‘A 4）
             （构建编码树
               （构建树叶 ‘B 2）
               （构建编码树 （构造树叶 ‘D 1）
                          （构造树叶 ‘C 1）））））
（定义 样例编码序列 ‘（0 1 1 0 0 1 0 1 0 1 1 1 0））

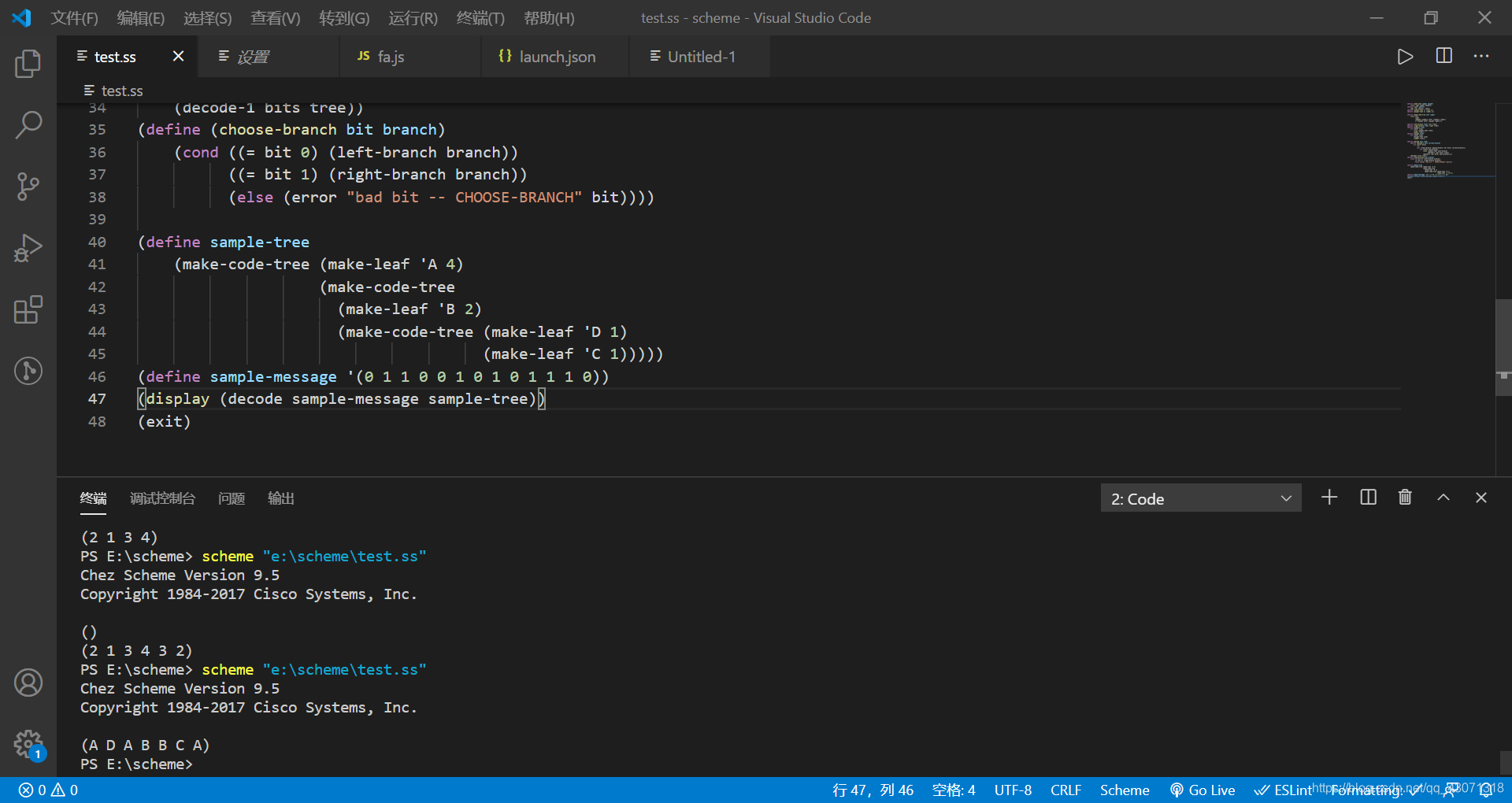
然后用decode完成该消息的编码，给出编码的结果。

解：

(define (make-leaf symbol weight)
    (list 'leaf symbol weight))
(define (leaf? object)
    (eq? (car object) 'leaf))
(define (symbol-leaf x) (cadr x))
(define (weight-leaf x) (caddr x))

(define (make-code-tree left right)
    (list left
          right
          (append (symbols left) (symbols right))
          (+ (weight left) (weight right))))

(define (left-branch tree) (car tree))
(define (right-branch tree) (cadr tree))
(define (symbols tree)
    (if (leaf? tree)
        (list (symbol-leaf tree))
        (caddr tree)))
(define (weight tree)
    (if (leaf? tree)
        (weight-leaf tree)
        (cadddr tree)))

(define (decode bits tree)
    (define (decode-1 bits current-branch)
        (if (null? bits)
            '()
            (let ((next-branch (choose-branch (car bits) current-branch)))
                (if (leaf? next-branch)
                    (cons (symbol-leaf next-branch)
                          (decode-1 (cdr bits) tree))
                    (decode-1 (cdr bits) next-branch)))))
    (decode-1 bits tree))
(define (choose-branch bit branch)
    (cond ((= bit 0) (left-branch branch))
          ((= bit 1) (right-branch branch))
          (else (error "bad bit -- CHOOSE-BRANCH" bit))))

(define sample-tree
    (make-code-tree (make-leaf 'A 4)
                    (make-code-tree
                      (make-leaf 'B 2)
                      (make-code-tree (make-leaf 'D 1)
                                      (make-leaf 'C 1)))))
(define sample-message '(0 1 1 0 0 1 0 1 0 1 1 1 0))
(display (decode sample-message sample-tree))
(exit)

(define (相同？ 甲 乙) (eq? 甲 乙))
(define (第一项 序列) (car 序列))
(define (第二项 序列) (cadr 序列))
(define (第三项 序列) (caddr 序列))
(define (第四项 序列) (cadddr 序列))
(define (到空值了？ 序列) (null? 序列))
(define (为空值？ 序列) (null? 序列))
(define (前头的项 序列) (car 序列))
(define (后面的项 序列) (cdr 序列))
(define (前项 序对) (car 序对))
(define (后项 序对) (cdr 序对))
(define (合并 甲序列 乙序列) (append 甲序列 乙序列))
(define (序对 前项 后项) (cons 前项 后项))
(define (构建序对 前项 后项) (cons 前项 后项))
(define (输出 内容) (display 内容))
(define (退出) (exit))

(define (构造树叶 符号 权重)
    (list '叶 符号 权重))
(define (是树叶？ 结点)
    (相同？ (第一项 结点) '叶))
(define (叶上符号 树叶) (第二项 树叶))
(define (叶的权重 树叶) (第三项 树叶))

(define (构建哈夫曼树 左分支 右分支)
    (list 左分支
          右分支
          (合并 (符号集 左分支) (符号集 右分支))
          (+ (权重 左分支) (权重 右分支))))

(define (左分支 哈夫曼树) (第一项 哈夫曼树))
(define (右分支 哈夫曼树) (第二项 哈夫曼树))
(define (符号集 哈夫曼树)
    (if (是树叶？ 哈夫曼树)
        (list (叶上符号 哈夫曼树))
        (第三项 哈夫曼树)))

(define (权重 哈夫曼树)
    (if (是树叶？ 哈夫曼树)
        (叶的权重 哈夫曼树)
        (第四项 哈夫曼树)))

(define (解码 零一序列 哈夫曼树)
    (define (执行解码 零一序列 当前分支)
        (if (到空值了？ 零一序列)
            '()
            (let ((下一分支 (选择分支 (第一项 零一序列) 当前分支)))
                (if (是树叶？ 下一分支)
                    (序对 (叶上符号 下一分支)
                          (执行解码 (后面的项 零一序列) 哈夫曼树))
                    (执行解码 (后面的项 零一序列) 下一分支)))))
    (执行解码 零一序列 哈夫曼树))
(define (选择分支 码值 当前分支)
    (cond ((= 码值 0) (左分支 当前分支))
          ((= 码值 1) (右分支 当前分支))
          (else (error "码值不是0或1" 码值))))

(define 样例哈夫曼树
    (构建哈夫曼树 (构造树叶 'A 4)
                 (构建哈夫曼树
                      (构造树叶 'B 2)
                      (构建哈夫曼树 (构造树叶 'D 1)
                                   (构造树叶 'C 1)))))
(define 消息序列 '(0 1 1 0 0 1 0 1 0 1 1 1 0))
(输出 (解码 消息序列 样例哈夫曼树))
(退出)

练习2.68
过程encode以一个消息和一棵树为参数，产生出被编码消息所对应的二进制位的表：

(define (encode message tree)
    (if (null? message)
        '()
        (append (encode-symbol (car message) tree)
                (encode (cdr message) tree))))

尝试将上述过程直译为汉语：

（定义 （编码 消息 哈夫曼树）
    （如果 （为空？ 消息）
           ‘（）
           （合并 （符号编码 （第一项 消息）哈夫曼树）
                 （编码 （后面的项 消息）哈夫曼树））））

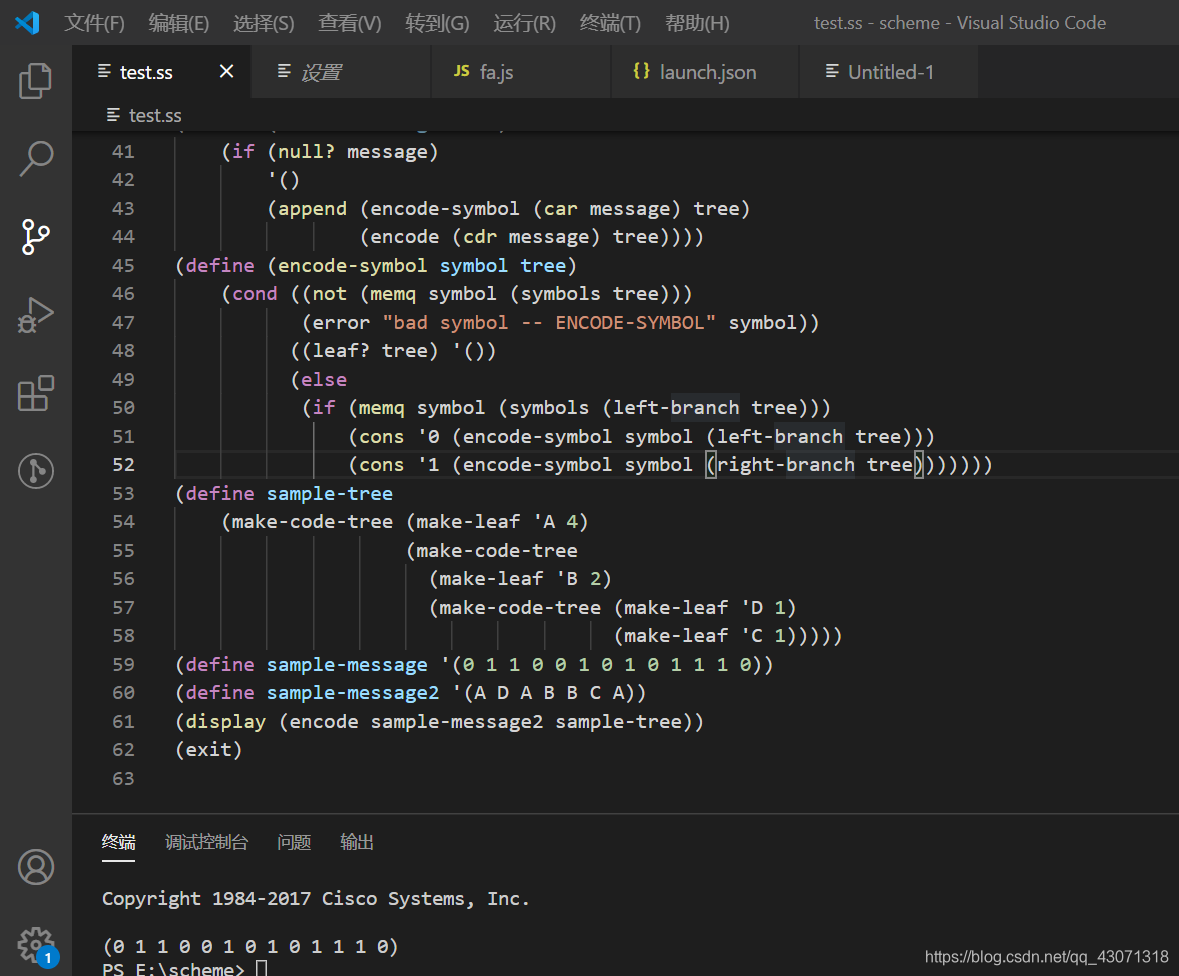
其中的encode-symbol是需要你写出的过程，它能根据给定的树产生出给定符号的二进制位表。你所设计的encode- symbol在遇到未出现在树中的符号时应报告错误。请用在练习2.67中得到的结果检查所实现的过程，工作中用同样一棵树，看看得到的结果是不是原来那个消息。

解：

(define (make-leaf symbol weight)
    (list 'leaf symbol weight))
(define (leaf? object)
    (eq? (car object) 'leaf))
(define (symbol-leaf x) (cadr x))
(define (weight-leaf x) (caddr x))

(define (make-code-tree left right)
    (list left
          right
          (append (symbols left) (symbols right))
          (+ (weight left) (weight right))))

(define (left-branch tree) (car tree))
(define (right-branch tree) (cadr tree))
(define (symbols tree)
    (if (leaf? tree)
        (list (symbol-leaf tree))
        (caddr tree)))
(define (weight tree)
    (if (leaf? tree)
        (weight-leaf tree)
        (cadddr tree)))

(define (decode bits tree)
    (define (decode-1 bits current-branch)
        (if (null? bits)
            '()
            (let ((next-branch (choose-branch (car bits) current-branch)))
                (if (leaf? next-branch)
                    (cons (symbol-leaf next-branch)
                          (decode-1 (cdr bits) tree))
                    (decode-1 (cdr bits) next-branch)))))
    (decode-1 bits tree))
(define (choose-branch bit branch)
    (cond ((= bit 0) (left-branch branch))
          ((= bit 1) (right-branch branch))
          (else (error "bad bit -- CHOOSE-BRANCH" bit))))

(define (encode message tree)
    (if (null? message)
        '()
        (append (encode-symbol (car message) tree)
                (encode (cdr message) tree))))
(define (encode-symbol symbol tree)
    (cond ((not (memq symbol (symbols tree)))
           (error "bad symbol -- ENCODE-SYMBOL" symbol))
          ((leaf? tree) '())
          (else
           (if (memq symbol (symbols (left-branch tree)))
               (cons '0 (encode-symbol symbol (left-branch tree)))
               (cons '1 (encode-symbol symbol (right-branch tree)))))))
(define sample-tree
    (make-code-tree (make-leaf 'A 4)
                    (make-code-tree
                      (make-leaf 'B 2)
                      (make-code-tree (make-leaf 'D 1)
                                      (make-leaf 'C 1)))))
(define sample-message '(0 1 1 0 0 1 0 1 0 1 1 1 0))
(define sample-message2 '(A D A B B C A))
(display (encode sample-message2 sample-tree))
(exit)

(define (相同？ 甲 乙) (eq? 甲 乙))
(define (第一项 序列) (car 序列))
(define (第二项 序列) (cadr 序列))
(define (第三项 序列) (caddr 序列))
(define (第四项 序列) (cadddr 序列))
(define (到空值了？ 序列) (null? 序列))
(define (为空值？ 序列) (null? 序列))
(define (前头的项 序列) (car 序列))
(define (后面的项 序列) (cdr 序列))
(define (前项 序对) (car 序对))
(define (后项 序对) (cdr 序对))
(define (合并 甲序列 乙序列) (append 甲序列 乙序列))
(define (序对 前项 后项) (cons 前项 后项))
(define (构建序对 前项 后项) (cons 前项 后项))
(define (包含 元 序列) (memq 元 序列))
(define (不 条件) (not 条件))
(define (错误 报错内容 参数) (error 报错内容 参数))
(define (输出 内容) (display 内容))
(define (退出) (exit))

(define (构造树叶 符号 权重)
    (list '叶 符号 权重))
(define (是树叶？ 结点)
    (相同？ (第一项 结点) '叶))
(define (到树叶了？ 树)
    (是树叶？ 树))
(define (叶上符号 树叶) (第二项 树叶))
(define (叶的权重 树叶) (第三项 树叶))

(define (构建哈夫曼树 左分支 右分支)
    (list 左分支
          右分支
          (合并 (符号集 左分支) (符号集 右分支))
          (+ (权重 左分支) (权重 右分支))))

(define (左分支 哈夫曼树) (第一项 哈夫曼树))
(define (右分支 哈夫曼树) (第二项 哈夫曼树))
(define (符号集 哈夫曼树)
    (if (是树叶？ 哈夫曼树)
        (list (叶上符号 哈夫曼树))
        (第三项 哈夫曼树)))

(define (权重 哈夫曼树)
    (if (是树叶？ 哈夫曼树)
        (叶的权重 哈夫曼树)
        (第四项 哈夫曼树)))

(define (解码 零一序列 哈夫曼树)
    (define (执行解码 零一序列 当前分支)
        (if (到空值了？ 零一序列)
            '()
            (let ((下一分支 (选择分支 (第一项 零一序列) 当前分支)))
                (if (是树叶？ 下一分支)
                    (序对 (叶上符号 下一分支)
                          (执行解码 (后面的项 零一序列) 哈夫曼树))
                    (执行解码 (后面的项 零一序列) 下一分支)))))
    (执行解码 零一序列 哈夫曼树))
(define (选择分支 码值 当前分支)
    (cond ((= 码值 0) (左分支 当前分支))
          ((= 码值 1) (右分支 当前分支))
          (else (error "码值不是0或1" 码值))))

(define (编码 消息 哈夫曼树)
    (if (到空值了？ 消息)
        '()
        (合并 (符号编码 (第一项 消息) 哈夫曼树)
              (编码 (后面的项 消息) 哈夫曼树))))
(define (符号编码 符号 哈夫曼树)
    (cond ((不 (包含 符号 (符号集 哈夫曼树)))
           (错误 "哈夫曼树中不包含这个符号" 符号))
          ((到树叶了？ 哈夫曼树) '())
          (else 
           (if (包含 符号 (符号集 (左分支 哈夫曼树)))
               (构建序对 '0 (符号编码 符号 (左分支 哈夫曼树)))
               (构建序对 '1 (符号编码 符号 (右分支 哈夫曼树)))))))
(define 样例哈夫曼树
    (构建哈夫曼树 (构造树叶 'A 4)
                 (构建哈夫曼树
                      (构造树叶 'B 2)
                      (构建哈夫曼树 (构造树叶 'D 1)
                                   (构造树叶 'C 1)))))
(define 零一序列 '(0 1 1 0 0 1 0 1 0 1 1 1 0))
(define 消息 '(A D A B B C A))
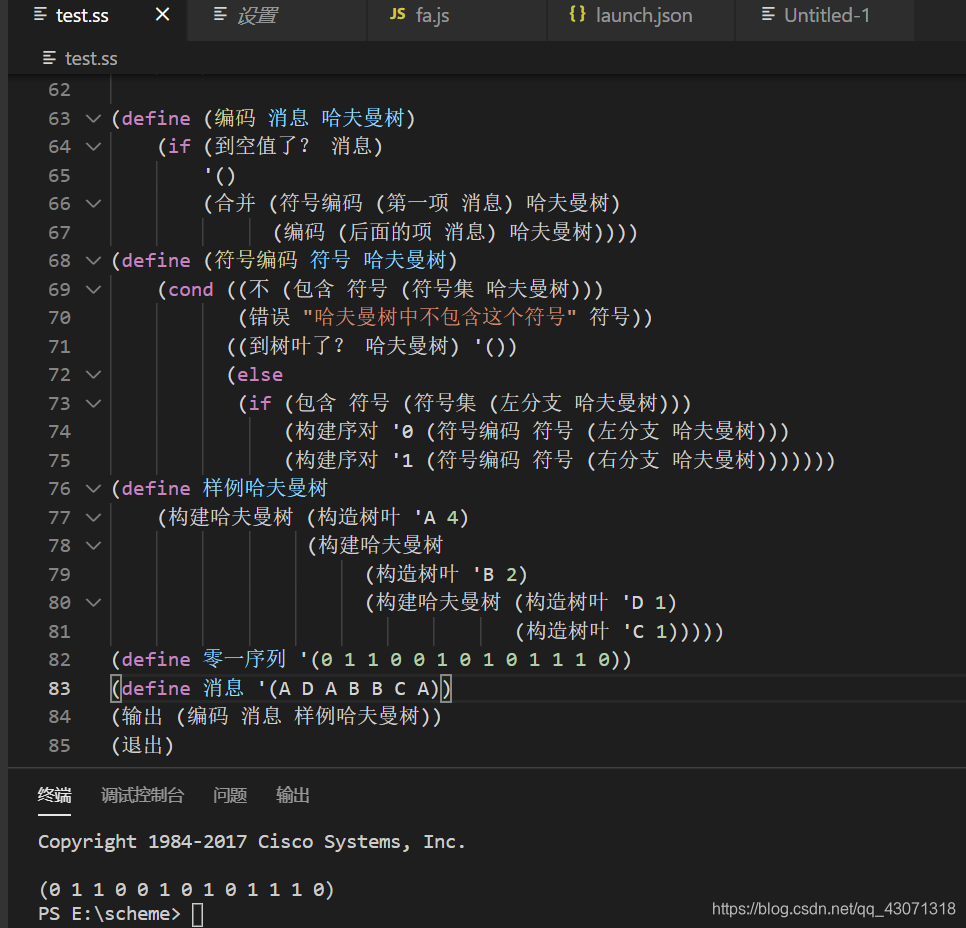
(输出 (编码 消息 样例哈夫曼树))
(退出)

练习2.69
下面过程以一个符号-频度对偶表为参数(其中没有任何符号出现在多于一个对偶中)，并根据Huffman算法生成出Huffman编码树。

(define (generate-huffman-tree pairs)
    (successive-merge (make-leaf-set pairs)))

其中的make-leaf-set是前面给出的过程，它将对偶表变换为叶的有序集，successive-merge是需要你写的过程，它使用make-code-tree反复归并集合中具有最小权重的元素，直至集合里只剩下一个元素为止。这个元素就是我们所需要的Huffman树。(这一过程稍微有点技巧性，但并不很复杂。如果你正在设计的过程变得很复杂，那么几乎可以肯定是在什么.地方搞错了。你应该尽可能地利用有序集合表示这一事实。)

解：

(define (make-leaf symbol weight)
  (list 'leaf symbol weight))

(define (leaf? object)
  (eq? (car object) 'leaf))

(define (symbol-leaf x) (cadr x))

(define (weight-leaf x) (caddr x))

(define (make-code-tree left right)
  (list left
        right
        (append (symbols left) (symbols right))
        (+ (weight left) (weight right))))

(define (left-branch tree) (car tree))

(define (right-branch tree) (cadr tree))

(define (symbols tree)
  (if (leaf? tree)
      (list (symbol-leaf tree))
      (caddr tree)))

(define (weight tree)
  (if (leaf? tree)
      (weight-leaf tree)
      (cadddr tree)))

(define (adjoin-set x set)
  (cond ((null? set) (list x))
        ((< (weight x) (weight (car set))) (cons x set))
        (else (cons (car set)
                    (adjoin-set x (cdr set))))))

(define (make-leaf-set pairs)
  (if (null? pairs)
      '()
      (let ((pair (car pairs)))
        (adjoin-set (make-leaf (car pair)
                               (cadr pair))
                    (make-leaf-set (cdr pairs))))))

(define (generate-huffman-tree pairs)
  (successive-merge (make-leaf-set pairs)))

(define (successive-merge tree-set)
  (if (= (length tree-set) 1)
      (car tree-set)
      (successive-merge (adjoin-set
                         (make-code-tree
                          (car tree-set) (cadr tree-set))
                         (cddr tree-set)))))

汉语命名版本：

(define (相同？ 甲 乙) (eq? 甲 乙))
(define (第一项 序列) (car 序列))
(define (第二项 序列) (cadr 序列))
(define (第三项 序列) (caddr 序列))
(define (第四项 序列) (cadddr 序列))
(define (到空值了？ 序列) (null? 序列))
(define (为空值？ 序列) (null? 序列))
(define (为空？ 序列) (null? 序列))
(define (元素个数 序列) (length 序列))
(define (前头的项 序列) (car 序列))
(define (后面的项 序列) (cdr 序列))
(define (前项 序对) (car 序对))
(define (后项 序对) (cdr 序对))
(define (第二项开始后面的项 序列) (cdr 序列))
(define (第一项后面的项 序列) (cdr 序列))
(define (第三项开始后面的项 序列) (cddr 序列))
(define (第二项后面的项 序列) (cddr 序列))
(define (合并 甲序列 乙序列) (append 甲序列 乙序列))
(define (序对 前项 后项) (cons 前项 后项))
(define (构建序对 前项 后项) (cons 前项 后项))
(define (包含 元 序列) (memq 元 序列))
(define (不 条件) (not 条件))
(define (错误 报错内容 参数) (error 报错内容 参数))
(define (输出 内容) (display 内容))
(define (退出) (exit))

(define (构造树叶 符号 权重)
    (list '叶 符号 权重))
(define (是树叶？ 结点)
    (相同？ (第一项 结点) '叶))
(define (到树叶了？ 树)
    (是树叶？ 树))
(define (叶上符号 树叶) (第二项 树叶))
(define (叶的权重 树叶) (第三项 树叶))

(define (构建哈夫曼树结构 左分支 右分支)
    (list 左分支
          右分支
          (合并 (符号集 左分支) (符号集 右分支))
          (+ (权重 左分支) (权重 右分支))))

(define (左分支 哈夫曼树) (第一项 哈夫曼树))
(define (右分支 哈夫曼树) (第二项 哈夫曼树))
(define (符号集 哈夫曼树)
    (if (是树叶？ 哈夫曼树)
        (list (叶上符号 哈夫曼树))
        (第三项 哈夫曼树)))

(define (权重 哈夫曼树)
    (if (是树叶？ 哈夫曼树)
        (叶的权重 哈夫曼树)
        (第四项 哈夫曼树)))

(define (解码 零一序列 哈夫曼树)
    (define (执行解码 零一序列 当前分支)
        (if (到空值了？ 零一序列)
            '()
            (let ((下一分支 (选择分支 (第一项 零一序列) 当前分支)))
                (if (是树叶？ 下一分支)
                    (序对 (叶上符号 下一分支)
                          (执行解码 (后面的项 零一序列) 哈夫曼树))
                    (执行解码 (后面的项 零一序列) 下一分支)))))
    (执行解码 零一序列 哈夫曼树))
(define (选择分支 码值 当前分支)
    (cond ((= 码值 0) (左分支 当前分支))
          ((= 码值 1) (右分支 当前分支))
          (else (error "码值不是0或1" 码值))))

(define (编码 消息 哈夫曼树)
    (if (到空值了？ 消息)
        '()
        (合并 (符号编码 (第一项 消息) 哈夫曼树)
              (编码 (第一项后面的项 消息) 哈夫曼树))))
(define (符号编码 符号 哈夫曼树)
    (cond ((不 (包含 符号 (符号集 哈夫曼树)))
           (错误 "哈夫曼树中不包含这个符号" 符号))
          ((到树叶了？ 哈夫曼树) '())
          (else 
           (if (包含 符号 (符号集 (左分支 哈夫曼树)))
               (构建序对 '0 (符号编码 符号 (左分支 哈夫曼树)))
               (构建序对 '1 (符号编码 符号 (右分支 哈夫曼树)))))))

(define (按权重插入 树 集合)
  (cond ((为空？ 集合) (list 树))
        ((< (权重 树) (权重 (第一项 集合))) (构建序对 树 集合))
        (else (构建序对 (第一项 集合)
                       (按权重插入 树 (第一项后面的项 集合))))))

(define (构建树叶集合 符号-频度对偶表)
  (if (到空值了？ 符号-频度对偶表)
      '()
      (let ((符号-频度对偶 (第一项 符号-频度对偶表)))
        (按权重插入  (构造树叶 (第一项 符号-频度对偶)
                             (第二项 符号-频度对偶))
                    (构建树叶集合 (第一项后面的项 符号-频度对偶表))))))

(define (生成哈夫曼树 符号-频度对偶表)
  (连续归并 (构建树叶集合 符号-频度对偶表)))

(define (连续归并 树集合)
  (if (= (元素个数 树集合) 1)
      (第一项 树集合)
      (连续归并 (按权重插入
                         (构建哈夫曼树结构
                          (第一项 树集合) (第二项 树集合))
                         (第二项后面的项 树集合)))))

(define 符号-频度对偶序列 '((A 4) (B 2) (C 1) (D 1)))
(输出 (生成哈夫曼树 符号-频度对偶序列))
(退出)

对于符号频度对偶序列“((A 4) (B 2) (C 1) (D 1)”执行构建树叶集合后，会得到：

((叶 D 1) (叶 C 1) (叶 B 2) (叶 A 4))

简化一下，把“叶”字省略，这个集合就是((D 1) (C 1) (B 2) (A 4))

（这么写纯属是我比较懒吧。。。感觉这么写足够分析了，一步步合并过程中，集合也不会变得很乱）

对上面这个初始叶子集合连续归并生成哈夫曼树的过程如下：

1.提取前两项，合并：

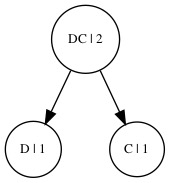
此时序列变为：
((B 2) (DC 2) (A 4))

2.提取前两项，合并：

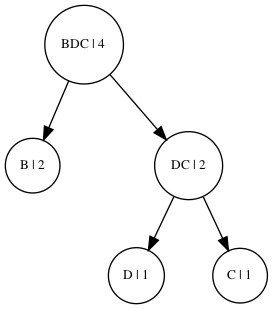
此时序列变为：
((A 4) (BDC 4) )

3.提取前两项，合并：

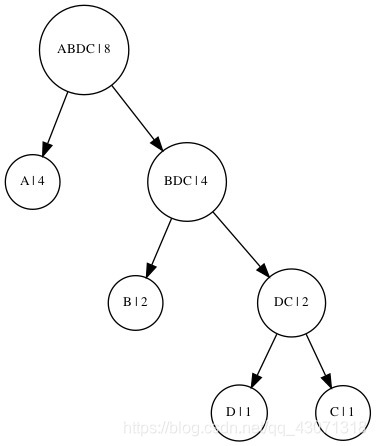
最终序列变为：((ABDC 8))

练习2.70
下面带有相对频度的8个符号的字母表，是为了有效编码20世纪50年代的摇滚歌曲中的词语而设计的。(请注意，“字母表”中的“符号”不必是单个字母。)

单词	频度
A	2
BOOM	1
NA	16
SHA	3
GET	2
JOB	2
YIP	9
WAH	1

请用(练习2.69 的) generate-huffman-tree过程生成对应的Huffman树，用(练习2.68的) encode过程编码下面的消息：

Get a job
Sha na na na na na na na na
Get a job
Sha na na na na na na na na
Wah yip yip yip yip yip yip yip yip yip
Sha boom

这一编码需要多少个二进制位?如果对这8个符号的字母表采用定长编码，完成这个歌曲的编码最少需要多少个二进制位?

解：

(define (相同？ 甲 乙) (eq? 甲 乙))
(define (第一项 序列) (car 序列))
(define (第二项 序列) (cadr 序列))
(define (第三项 序列) (caddr 序列))
(define (第四项 序列) (cadddr 序列))
(define (到空值了？ 序列) (null? 序列))
(define (为空值？ 序列) (null? 序列))
(define (为空？ 序列) (null? 序列))
(define (元素个数 序列) (length 序列))
(define (前头的项 序列) (car 序列))
(define (后面的项 序列) (cdr 序列))
(define (前项 序对) (car 序对))
(define (后项 序对) (cdr 序对))
(define (第二项开始后面的项 序列) (cdr 序列))
(define (第一项后面的项 序列) (cdr 序列))
(define (第三项开始后面的项 序列) (cddr 序列))
(define (第二项后面的项 序列) (cddr 序列))
(define (合并 甲序列 乙序列) (append 甲序列 乙序列))
(define (序对 前项 后项) (cons 前项 后项))
(define (构建序对 前项 后项) (cons 前项 后项))
(define (包含 元 序列) (memq 元 序列))
(define (不 条件) (not 条件))
(define (错误 报错内容 参数) (error 报错内容 参数))
(define (输出 内容) (display 内容))
(define (退出) (exit))

(define (构造树叶 符号 权重)
    (list '叶 符号 权重))
(define (是树叶？ 结点)
    (相同？ (第一项 结点) '叶))
(define (到树叶了？ 树)
    (是树叶？ 树))
(define (叶上符号 树叶) (第二项 树叶))
(define (叶的权重 树叶) (第三项 树叶))

(define (构建哈夫曼树结构 左分支 右分支)
    (list 左分支
          右分支
          (合并 (符号集 左分支) (符号集 右分支))
          (+ (权重 左分支) (权重 右分支))))

(define (左分支 哈夫曼树) (第一项 哈夫曼树))
(define (右分支 哈夫曼树) (第二项 哈夫曼树))
(define (符号集 哈夫曼树)
    (if (是树叶？ 哈夫曼树)
        (list (叶上符号 哈夫曼树))
        (第三项 哈夫曼树)))

(define (权重 哈夫曼树)
    (if (是树叶？ 哈夫曼树)
        (叶的权重 哈夫曼树)
        (第四项 哈夫曼树)))

(define (解码 零一序列 哈夫曼树)
    (define (执行解码 零一序列 当前分支)
        (if (到空值了？ 零一序列)
            '()
            (let ((下一分支 (选择分支 (第一项 零一序列) 当前分支)))
                (if (是树叶？ 下一分支)
                    (序对 (叶上符号 下一分支)
                          (执行解码 (后面的项 零一序列) 哈夫曼树))
                    (执行解码 (后面的项 零一序列) 下一分支)))))
    (执行解码 零一序列 哈夫曼树))
(define (选择分支 码值 当前分支)
    (cond ((= 码值 0) (左分支 当前分支))
          ((= 码值 1) (右分支 当前分支))
          (else (error "码值不是0或1" 码值))))

(define (编码 消息 哈夫曼树)
    (if (到空值了？ 消息)
        '()
        (合并 (符号编码 (第一项 消息) 哈夫曼树)
              (编码 (第一项后面的项 消息) 哈夫曼树))))
(define (符号编码 符号 哈夫曼树)
    (cond ((不 (包含 符号 (符号集 哈夫曼树)))
           (错误 "哈夫曼树中不包含这个符号" 符号))
          ((到树叶了？ 哈夫曼树) '())
          (else 
           (if (包含 符号 (符号集 (左分支 哈夫曼树)))
               (构建序对 '0 (符号编码 符号 (左分支 哈夫曼树)))
               (构建序对 '1 (符号编码 符号 (右分支 哈夫曼树)))))))

(define (按权重插入 树 集合)
  (cond ((为空？ 集合) (list 树))
        ((< (权重 树) (权重 (第一项 集合))) (构建序对 树 集合))
        (else (构建序对 (第一项 集合)
                       (按权重插入 树 (第一项后面的项 集合))))))

(define (构建树叶集合 符号-频度对偶表)
  (if (到空值了？ 符号-频度对偶表)
      '()
      (let ((符号-频度对偶 (第一项 符号-频度对偶表)))
        (按权重插入  (构造树叶 (第一项 符号-频度对偶)
                             (第二项 符号-频度对偶))
                    (构建树叶集合 (第一项后面的项 符号-频度对偶表))))))

(define (生成哈夫曼树 符号-频度对偶表)
  (连续归并 (构建树叶集合 符号-频度对偶表)))

(define (连续归并 树集合)
  (if (= (元素个数 树集合) 1)
      (第一项 树集合)
      (连续归并 (按权重插入
                         (构建哈夫曼树结构
                          (第一项 树集合) (第二项 树集合))
                         (第二项后面的项 树集合)))))

(define 符号-频度对偶序列 '((A 2) (NA 16) (BOOM 1) (SHA 3) (GET 2) (YIP 9) (JOB 2) (WAH 1)))
(define 50年代美国摇滚哈夫曼树 (生成哈夫曼树 符号-频度对偶序列))
(define 消息 '(GET A JOB 
SHA NA NA NA NA NA NA NA NA NA
GET A JOB 
SHA NA NA NA NA NA NA NA NA NA
WAH YIP YIP YIP YIP YIP YIP YIP YIP YIP
SHA BOOM))
(输出 (编码 消息 50年代美国摇滚哈夫曼树))
(退出)

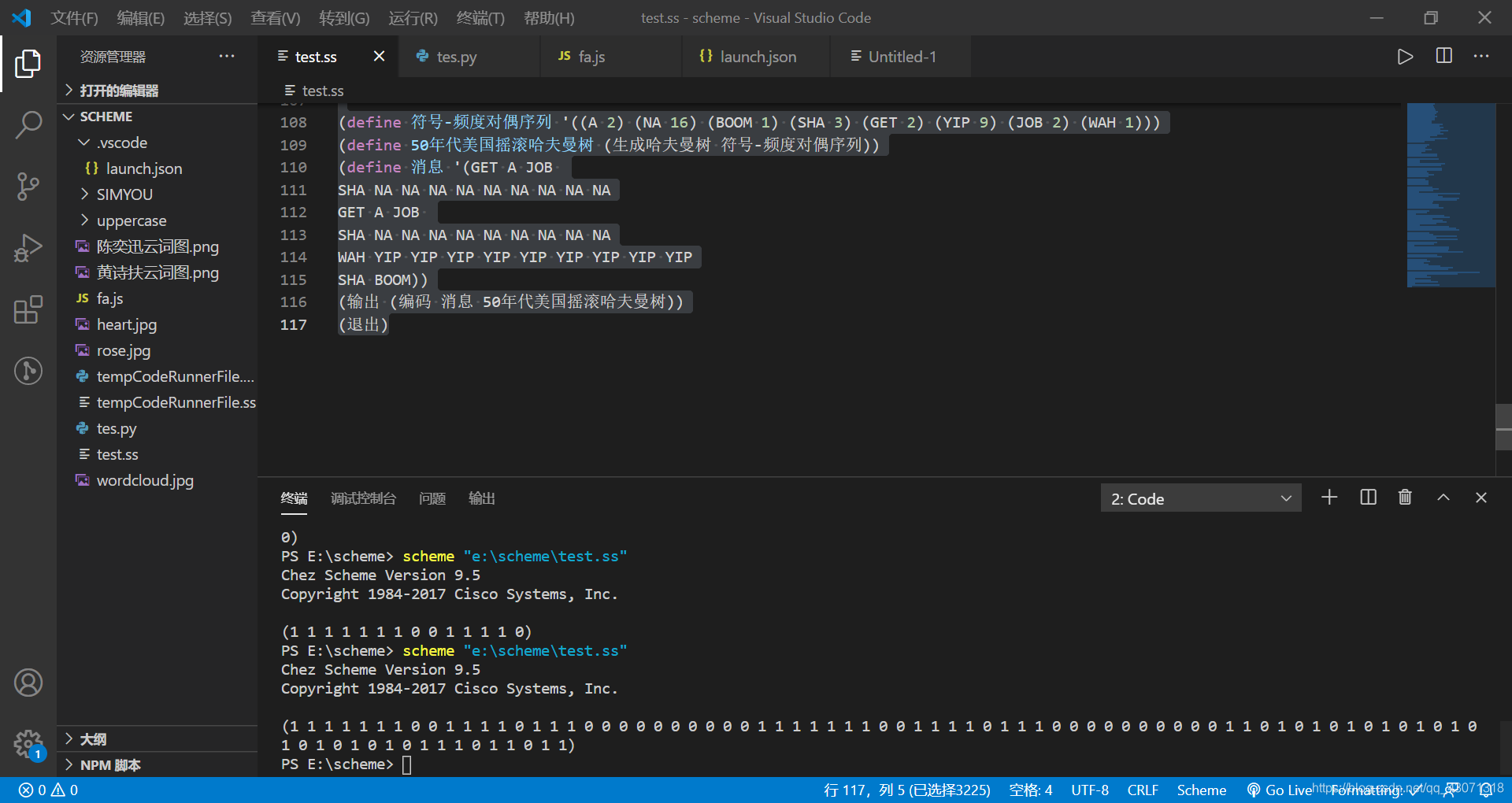
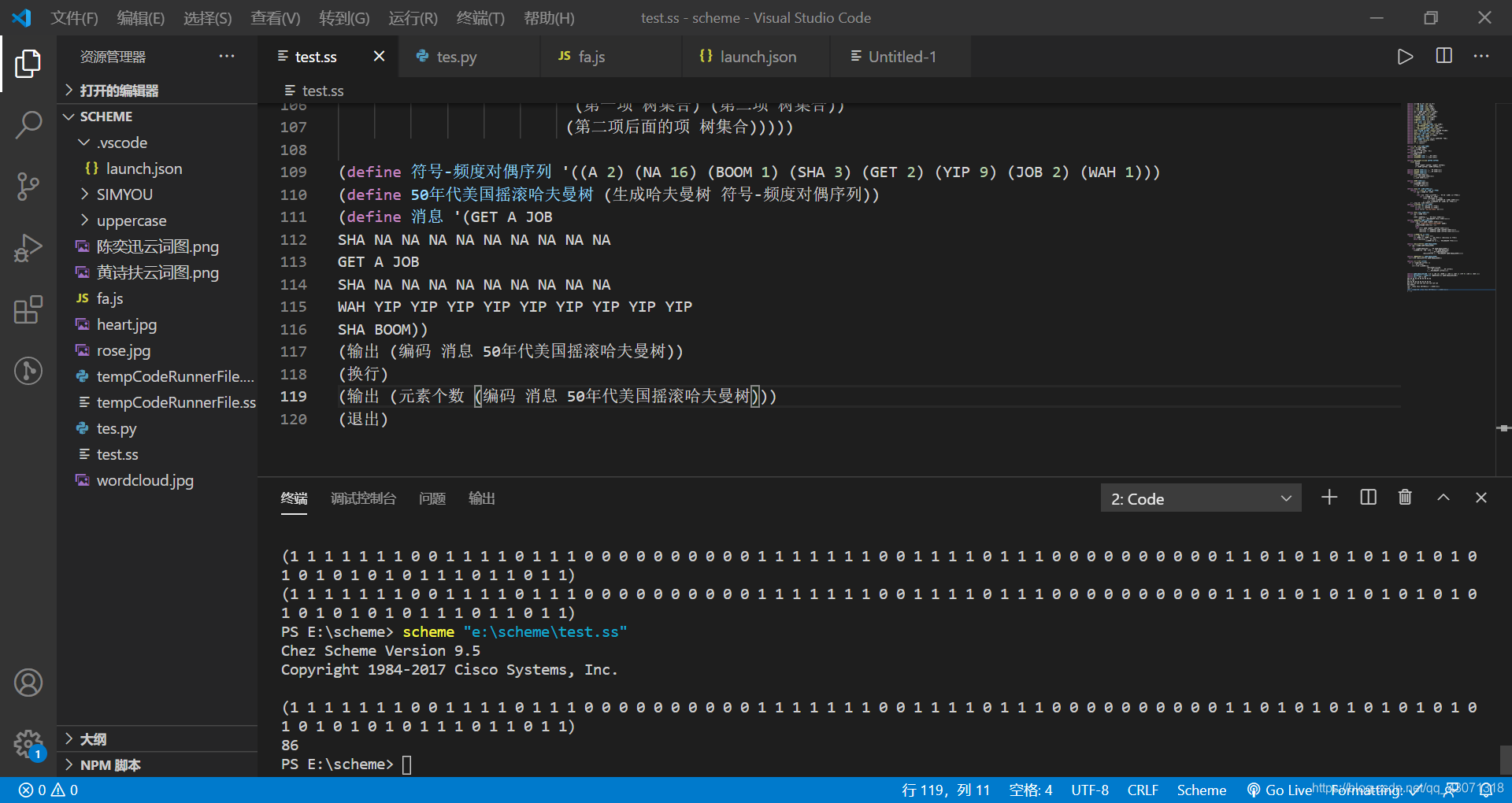
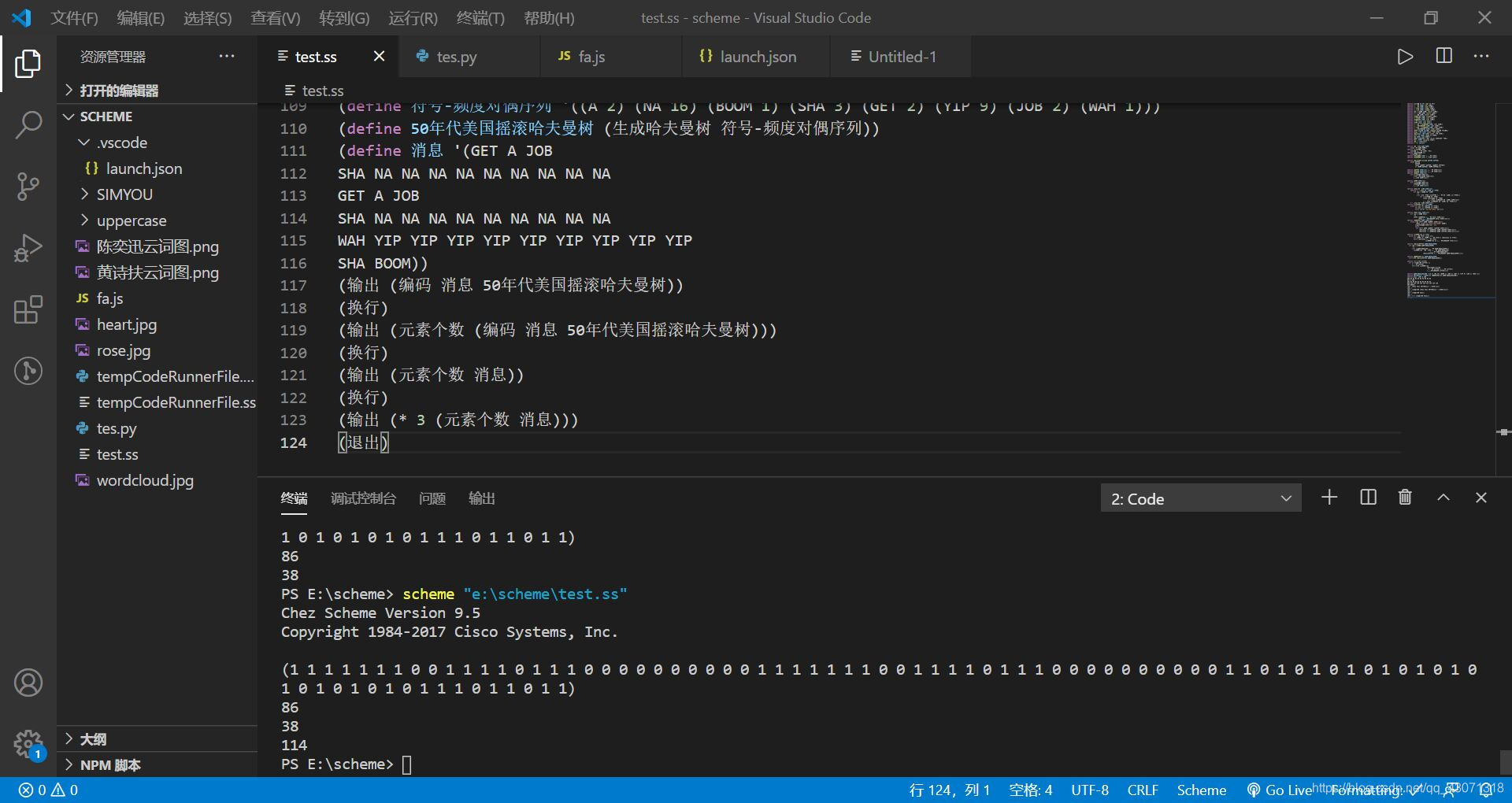
由上图可见一共用了86个二进制位；如果采用定长编码，一共8个单词，每个单词就是需要3位二进制位，一共38个单词，也就需要3 * 38 = 114位二进制位：

练习2.71
假定我们有一棵n个符号的字母表的Huffman树，其中各符号的相对频度分别是1，2，4，…，$2^{(n-1)}$。 请对n = 5和n= 10勾勒出有关的树的样子。对于这样的树(对于一般的n)，编码出现最频繁的符号用多少个二进制位？最不频繁的符号呢？

解：
对n=5，生成出的树的图像长这样：

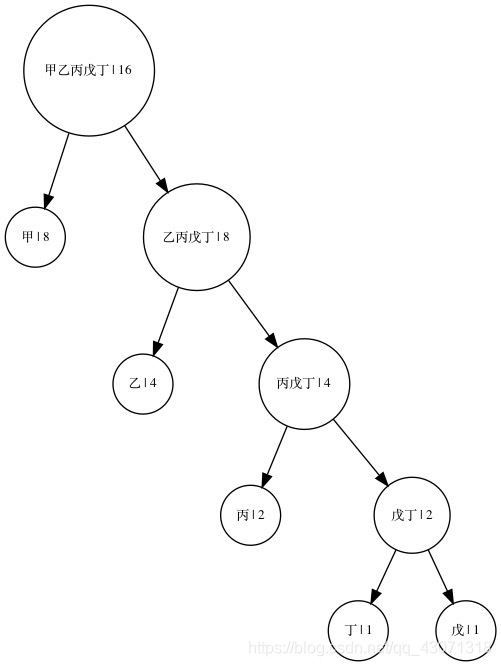
在有五个符号时，最频繁的符号编码需要一位，最不频繁的符号编码需要4位。

十个符号的脑补的出来……反正最频繁的符号编码需要一位，最不频繁的符号编码需要“个数-1”位。

练习2.72
考虑你在练习2.68中设计的编码过程。对于一个符号的编码，计算步数的增长速率是什么？请注意，这时需要把在每个结点中检查符号表所需的步数包括在内。一般性地回答这一问题是非常困难的。现在考虑一类特殊情况，其中的n个符号的相对频度如练习2.71所描述的。请给出编码最频繁的符号所需的步数和最不频繁的符号所需的步数的增长速度(作为n的函数)。

解：
判断符号在编码树中 Θ(𝑛)，树的平均深度 log(𝑛)，增长速率 Θ(𝑛log(𝑛))。

在 练习 2.71 中，最好的情况下，搜索深度为 1，最坏的情况为 𝑛−1，因此所需的步数分别为 Θ(𝑛)、Θ(𝑛2)。

参考文献：
[1] [美]Julie Sussman.计算机程序的构造和解释[M]. 裘宗燕译注.北京：机械工业出版社，1996.