线性回归

似然函数

概率表示为：P(x|θ)
是条件概率的表示方法，θ是前置条件，理解为在θ 的前提下，事件 x 发生的概率

似然表示为：L(x|θ)
理解为已知结果为 x ，参数为θ (似然函数里θ 是变量，这里说的参数是相对与概率而言的)对应的概率，即

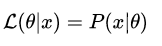
两者在数值上相等，但是意义并不相同。L(x|θ)是关于 θ 的函数，而P(x|θ) 则是关于 x 的函数，两者从不同的角度描述一件事情。

以伯努利分布（Bernoulli distribution，又叫做两点分布或0-1分布）为例：

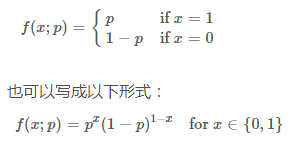
这里注意区分f(x;p) 与前面的条件概率的区别，引号后的 p 仅表示 f 依赖于 p 的值，p 并不是 f 的前置条件，而只是这个概率分布的一个参数而已，也可以省略引号后的内容。

从似然的角度出发，假设我们观测到的结果是 x=0.5x=0.5（即某一面朝上的概率是50%，这个结果可能是通过几千次几万次的试验得到的，总之我们现在知道这个结论），可以得到以下的似然函数：
与概率分布图不同的是，似然函数是一个(0, 1)内连续的函数，所以得到的图也是连续的，我们很容易看出似然函数的极值（也是最大值）在 p=0.5 处得到，通常不需要做图来观察极值，令似然函数的偏导数为零即可求得极值条件。

ps. 似然函数里的 p 描述的是硬币的性质而非事件发生的概率（比如 p=0.5 描述的是一枚两面均匀的硬币）。

让我们回到似然的定义，似然描述的是结果已知的情况下，该事件在不同条件下发生的可能性，似然函数的值越大，说明该发生事件的条件为p的可能性越大。

涉及到多个独立事件，在似然函数的表达式中通常都会出现连乘：

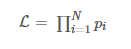
对多项乘积的求导往往非常复杂，但是对于多项求和的求导却要简单的多，对数函数不改变原函数的单调性和极值位置，而且根据对数函数的性质可以将乘积转换为加减式，这可以大大简化求导的过程：

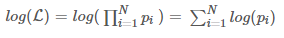
似然函数：https://blog.csdn.net/u014182497/article/details/82252456

高斯分布

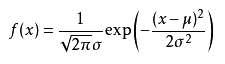
位置参数为μ、尺度参数为 σ

线性回归

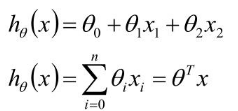
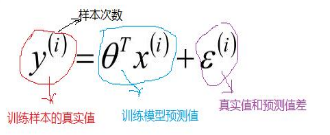
根据中心极限定律可以得到 ε 满足高斯分布的，u =0。



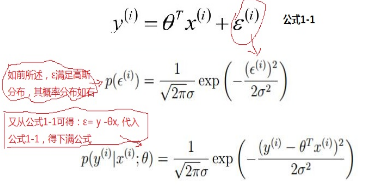
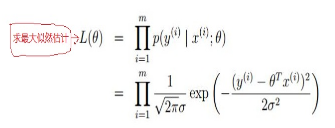
阶段性的总结：线性回归，根据大数定律和中心极限定律假定样本无穷大的时候，其真实值和预测值的误差ε 的加和服从u=0,方差=δ²的高斯分布且独立同分布，然后把ε =y-Øx 代入公式，就可以化简得到线性回归的损失函数。

第一种解法：

必须要满足可逆条件
第二种：梯度下降

逻辑回归

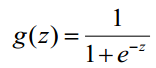
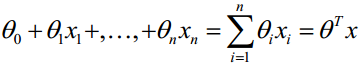
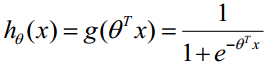
函数h（x）的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

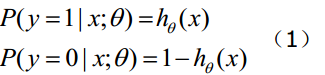
（1）综合起来：

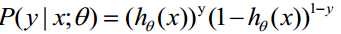
取似然函数：

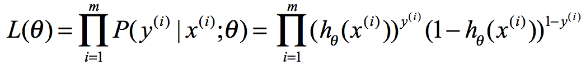
取对数：

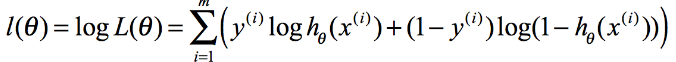
转化为梯度下降：

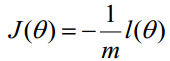
参考：https://blog.csdn.net/pakko/article/details/37878837

LR的归一化
值得一提的是求解LR模型过程中，每一个数据点对分类平面都是有影响的，它的影响力远离它到分类平面的距离指数递减。换句话说，LR的解是受数据本身分布影响的。在实际应用中，如果数据维度很高，LR模型都会配合参数的L1 regularization。

要说有什么本质区别，那就是两个模型对数据和参数的敏感程度不同，Linear SVM比较依赖penalty的系数和数据表达空间的测度，而（带正则项的）LR比较依赖对参数做L1 regularization的系数。但是由于他们或多或少都是线性分类器，所以实际上对低维度数据overfitting的能力都比较有限，相比之下对高维度数据，LR的表现会更加稳定，为什么呢？
因为Linear SVM在计算margin有多“宽”的时候是依赖数据表达上的距离测度(可以理解为度量标准,即在什么样的标准上计算gap的大小)的，换句话说如果这个测度不好（badly scaled，这种情况在高维数据尤为显著），所求得的所谓Large margin就没有意义了，这个问题即使换用kernel trick（比如用Gaussian kernel）也无法完全避免。所以使用Linear SVM之前一般都需要先对数据做normalization，(这里的normalization是对数据的归一化,注意区分之前的LR在类别不平衡的时候做的balancing)而求解LR（without regularization）时则不需要或者结果不敏感。
同时会有：feature scaling会使得gradient descent的收敛更好。
如果不归一化，各维特征的跨度差距很大，目标函数就会是“扁”的：

（图中椭圆表示目标函数的等高线，两个坐标轴代表两个特征）
这样feature scaling之后，在进行梯度下降的时候，梯度的方向就会偏离最小值的方向，走很多弯路。
如果归一化了，那么目标函数就“圆”了：

每一步梯度的方向都基本指向最小值，可以大踏步地前进。