算法背景
Tarjan算法是由Robert Tarjan(罗伯特·塔扬,不知有几位大神读对过这个名字) 发明的求有向图中强连通分量的算法。
预备知识点
有向图强连通分量:在有向图G中,如果两个顶点vi,vj间(vi>vj)有一条从vi到vj的有向路径,同时还有一条从vj到vi的有向路径,则称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通,称G是一个强连通图。有向图的极大强连通子图,称为强连通分量(strongly connected components)。
搜索树:将每个顶点只访问一次形成的树,如果图不连通就形成森林。
eg:

画成搜索树后

DFN[]数组,查找到当前节点的时间戳,这个数值是不能变的。
LOW[]数组,能够通过不在搜索树上的边回到最早的父节点的时间戳。不断的更新,使其一直是最小的。
visited[]数组,标记数组,如果标记代表这个节点在当前连通分量里面。后面提到的标记都是使用这个数组。
算法过程
通过dfs来递归查找子节点标记并压入栈s中,直到无法找到新的节点,然后判断LOW[v]是不是等于DFN[v]。为什么呢?上面说了LOW[v]是当前节点能够连通的最早的父节点,而DFN[v]是时间戳,也就是被深搜到的时间,那二者相等说明了这个点是一个强连通分量的根节点。
上面说到这条路已经走不下去了,那么就在v!=s.top()的条件下不断地pop,并且把标记取消,表明这个节点不在栈里面了。然后再回到上一层继续深搜。不断地进行下去
来一发图解

初始:ans = 0;
从1节点开始深搜 DFN[1] = LOW[1] = ++ans = 1
1搜索到2 DFN[2] = LOW[2] = ++ans = 2,如图

然后2节点深搜到3
所以DFN[3] = LOW[3] = ++ans = 3, 如图

3查找到6节点,所以
DFN[6] = LOW[6] = ++ans = 4, 如图
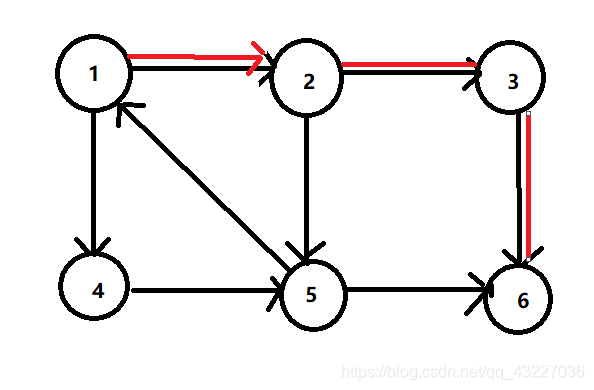
然后发现6节点是死路了,这时候判断发现DFN[6] == LOW[6], 所以直接输出6. 回退到3,判断LOW[3] 和LOW[6]的大小,发现LOW[3]小,所以LOW[3]不变,搜索发现也没有点了,再输出3。
回退到2,判断LOW[2]和LOW[3],LOW[2]小,所以LOW[2]值不变。
从2再次搜索到5
DFN[5] = LOW[5] = ++ans = 5, 如图
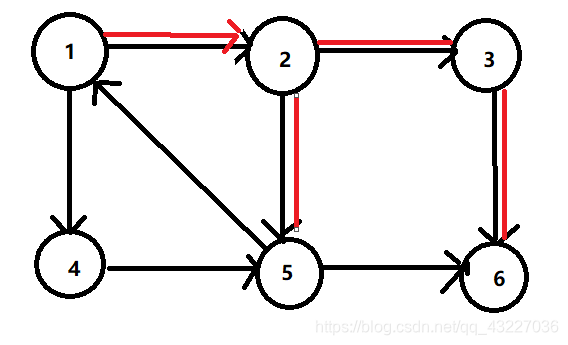
5先搜索到6,发现6的DFN值不为0,也就是已经搜索过了,然后又发现6并没有被标记过,那就说明这个节点属于其他连通分量,不再理它。
然后查找到了1,同样1的DFN值也不为0,但是1还在被标记的状态中,说明1属于当前这个连通分量。所以直接进行判断DFN[1]和LOW[5]的值谁的小。然后LOW[5]变为1,说明它现在不经过搜索树的父子边能够向上连通的最早的分量是1。
如图所示

这时候回退到2,然后判断LOW[2]和LOW[5]的值,更新LOW[2]值为1。2已经没可以搜索的点了,就判断LOW[2]和DFN[2]相不相等,不相等,证明2不是当前连通分量根节点,退回到1。
1又搜索到了4,DFN[4] = LOW[4] = ++ans = 6,
然后4搜索到了5,5的DFN值不为零并且5还在标记中。所以判断DFN[5]和LOW[4]的大小,修改LOW[4]为5。
回退到1,判断LOW[1]和LOW[4]的大小关系。然后判断LOW[1]和DFN[1]相不相等,发现相等,执行出栈操作。
整个过程搜索完毕。
代码实现
测试数据:
输入:
6 8
1 2
2 3
3 6
2 5
5 6
5 1
1 4
4 5
输出:
6
3
4 5 2 1
#include <iostream>
#include <vector>
#include <stack>
#include <cstring>
using namespace std;
const int MAX_V = 500001;
int DFN[MAX_V], visited[MAX_V], LOW[MAX_V];
int n, m;
struct edge
{
int to;
};
vector<edge>G[MAX_V];
void add_edge(int from, int to)
{
G[from].push_back((edge){to});
}
stack<int> s;
int ans = 0;
bool tarjan(int v)
{
s.push(v);
visited[v] = 1;
DFN[v] = LOW[v] = ++ans;
for (int i=0; i<G[v].size(); i++)
{
edge &e = G[v][i];
if (!DFN[e.to])
{
tarjan(e.to);
LOW[v] = min(LOW[v], LOW[e.to]);
}
else if (visited[e.to])
{
LOW[v] = min(LOW[v], DFN[e.to]);
}
}
if (DFN[v] == LOW[v])
{
int num = 0, temp;
do
{
num++;
temp = s.top();
cout << temp << " ";
s.pop();
visited[temp] = 0;
}while (v != temp);
cout << endl;
}
}
int main()
{
while (scanf("%d %d", &n, &m) && (n+m))
{
memset(visited, 0, sizeof(visited));
memset(DFN, 0, sizeof(DFN));
memset(LOW, 0, sizeof(LOW));
for (int i=1; i<=n; i++)
{
G[i].clear();
}
for (int i=0; i<m; i++)
{
int x, y;
scanf("%d %d", &x, &y);
add_edge(x, y);
}
for (int i=1; i<=n; i++)
{
if (!DFN[i])
{
tarjan(i);
}
}
}
return 0;
}
桥的判断
下面就到了我们的桥的判断,什么是桥呢?
如果一张无向图图去掉一条边后分成两个图,那这个边就是一个桥。
Eg:

显而易见边<4, 5>就是一个桥。
从图上我们能够直观的判断出一个边是不是桥,那怎么用tarjan算法去判断它是不是一个桥呢?
很简单,对于边<v, u>。只要满足 DFN[v] < LOW[u]就证明这条边是一个桥。为什么呢?根据两个数组的定义,LOW[u] > DFN[v]说明了u点在不通过<v, u>这条边的情况下,是无论如何也无法到达v点的。所以这两个点一定在两个连通分量里面,因此他们俩的边一定是一个桥。
由于这是一个无向图,我们一定会搜索到一个节点的父节点,我们又不能通过这条边来更新LOW值,这要怎么解决呢?
存图的时候把双向边存放在一起,也就是偶数如2,4,6,等位置放正向边,而3,5,7等位置放反向边, 并且2和3是互为反向边。在tarjan函数参数列表里多传一个参数,为父节点和当前节点边的值fa,当子节点搜索到一个点后,如果这个点被搜索过了,也就是DFN不为零了,进行判断i和fa的关系,如果i==fa^1的话,fa就是i的父节点,不理他。如果不是就更新LOW[v]的值。
对于^运算,能够快捷的判断这两条边是不是一对反向边。
如果n是偶数,那么n ^ 1的结果为n+1,。
如果n是奇数,那么n^1就是n-1。正好是一对一对的关系。
下面还是说一说存图的技巧吧,如果你看了上一个算法你会发现,我根本没有用到网上的head数组。就我个人理解而言,如果这个算法不需要边的作用,就使用上面的方法就行,简单易懂。
这个桥的判定就不一样了,总是用到边的关系,就需要我们使用head数组进行存图的边值,也就是给每条边一个编号。具体head数组怎么用呢?看代码。
在add_edge函数中是这样写的
void add_edge(int from, int to)
{
G[++len].to = to;
G[len].next = head[from];
Head[from] = len;
}
在具体的查找图的算法中是这样使用的
for (int i=head[v]; i; i=G[i].next)
接下来就是查找桥的算法了。
#include <iostream>
#include <cstring>
using namespace std;
const int MAX_V = 1005;
int DFN[MAX_V], LOW[MAX_V], head[MAX_V*MAX_V], bridge[MAX_V*MAX_V];
int len = 1, ans = 0;
struct edge
{
int y, next, cost;
}G[MAX_V*MAX_V];
void add_edge(int from, int to)
{
G[++len].y = to;
G[len].next = head[from];
head[from] = len;
}
void tarjan(int v, int v_bridge)
{
DFN[v] = LOW[v] = ++ans;
for (int i=head[v]; i; i=G[i].next)
{
int to = G[i].y;
if (!DFN[to])
{
tarjan(to, i);
LOW[v] = min(LOW[v], LOW[to]);
if (DFN[v] < LOW[to])
{
bridge[i] = bridge[i^1] = 1;
}
}
else if (i != (v_bridge^1))
{
LOW[v] = min(LOW[v], DFN[to]);
}
}
}
int main()
{
int n, m;
cin >> n >> m;
for (int i=0; i<m; i++)
{
int x, y;
cin >> x >> y;
add_edge(x, y);
add_edge(y, x);
}
for (int i=1; i<=n; i++)
{
if (!DFN[i])
{
tarjan(i, 0);
}
}
for (int i=2; i<len; i+=2)
{
if (bridge[i])
{
cout << G[i^1].y << " " << G[i].y << endl;
}
}
return 0;
}
对于上图例子
输入:
8 9
1 2
2 3
3 4
4 1
4 5
5 6
6 7
7 8
8 5
输出:
4 5
例题
一道桥判断的题。
地址
题目大意
在赤壁战役中,曹操被诸葛亮和周瑜击败。但是他不会放弃。曹操的部队仍不擅长水战,因此他想出了另一个主意。他在长江上建了许多岛屿,在这些岛屿的基础上,曹操的军队可以轻松地攻击周瑜的部队。曹操还修建了连接各岛的桥梁。如果所有岛屿都通过桥梁连接起来,那么曹操的军队可以很方便地在这些岛屿之间部署。周瑜不能忍受,所以他想摧毁一些草桥,以使一个或多个岛屿与其他岛屿分开。但是周瑜只有诸葛亮留下的一颗炸弹,所以他只能摧毁一座桥。周瑜必须派人携带炸弹摧毁这座桥。桥梁上可能会有警卫。轰炸队的士兵人数不得少于桥梁的守卫人数,否则任务将失败。请至少弄清楚周瑜必须派多少士兵来完成离岛任务。
解题思路
很明显就是用桥判断来进行做题,但需要注意的是,如果给出的图不是一个完整的图,直接输出0,如果桥上一个敌人也没有,输出1,因为至少有一个人要去炸桥。不要去掉重边,没说两座岛之间只允许有一座桥。
AC代码
#include <iostream>
#include <cstring>
#define mem(a) memset(a, 0, sizeof(a))
using namespace std;
const int MAX_V = 1005;
int DFN[MAX_V], LOW[MAX_V], head[MAX_V*MAX_V], bridge[MAX_V*MAX_V];
int len = 1, ans = 0;
struct edge
{
int y, next, cost;
}G[MAX_V*MAX_V];
void add_edge(int from, int to, int cost)
{
G[++len].y = to;
G[len].next = head[from];
G[len].cost = cost;
head[from] = len;
}
void tarjan(int v, int v_bridge)
{
DFN[v] = LOW[v] = ++ans;
for (int i=head[v]; i; i=G[i].next)
{
int to = G[i].y;
if (!DFN[to])
{
tarjan(to, i);
LOW[v] = min(LOW[v], LOW[to]);
if (DFN[v] < LOW[to])
{
bridge[i] = bridge[i^1] = 1;
}
}
else if (i != (v_bridge^1))
{
LOW[v] = min(LOW[v], DFN[to]);
}
}
}
int main()
{
ios::sync_with_stdio(false);
int n, m;
while (cin >> n >> m && (n+m))
{
ans = 0, len = 1;
mem(DFN);
mem(LOW);
mem(head);
mem(bridge);
for (int i=0; i<m; i++)
{
int x, y, cost;
cin >> x >> y >> cost;
add_edge(x, y, cost);
add_edge(y, x, cost);
}
int temp = 0;
for (int i=1; i<=n; i++)
{
if (!DFN[i])
{
temp++;
tarjan(i, 0);
}
}
if (temp > 1)
{
cout << 0 << endl;
}
else
{
int minnum = 0x3f3f3f3f;
bool flag = true;
for (int i=2; i<len; i+=2)
{
if (bridge[i] && G[i].cost < minnum)
{
minnum = G[i].cost;
flag = false;
}
}
if (!flag)
{
if (minnum != 0)
cout << minnum << endl;
else
cout << 1 << endl;
}
else
cout << "-1" << endl;
}
}
return 0;
}
割点判断
什么是割点呢?在一个无向图中,如果有一个顶点集合,删除这个顶点集合以及这个集合中所有顶点相关联的边以后,图的连通分量增多,就称这个点集为割点集合。如果某个割点集合只含有一个顶点X(也即{X}是一个割点集合),那么X称为一个割点。
割点是怎么判断的呢?上面我们知道了桥的判断方法是LOW[to] > DFN[from],根据割点的定义可以知道它是可以回到回到父节点的,所以就是LOW[to] >= DFN[from]。对于割点来说不用担心重边以及父节点问题,因为这并不影响它作为割点的性质,那么在DFN[to]不等于0时就可以直接更新LOW[from]值。需要注意的是,如果from节点是搜索树根节点的话,会至少有两个节点满足条件,所以需要判断一下
割点是不需要边的关系的,直接使用最开始的vector存图就可以了。
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
const int MAX_V = 100005;
bool cut[MAX_V];
int DFN[MAX_V], LOW[MAX_V];
int len = 1;
struct edge
{
int to;
};
vector<edge> G[MAX_V];
void add_edge(int from, int to)
{
G[from].push_back((edge){to});
}
int ans = 0;
int root;
void tarjan(int v)
{
DFN[v] = LOW[v] = ++ans;
int flag = 0;
for (int i=0; i<G[v].size(); i++)
{
int to = G[v][i].to;
if (!DFN[to])
{
tarjan(to);
LOW[v] = min(LOW[to], LOW[v]);
if (LOW[to] >= DFN[v])
{
flag++;
if (flag > 1 || v != root)
cut[v] = true;
}
}
else
{
LOW[v] = min(LOW[v], DFN[to]);
}
}
}
int main()
{
int n, m;
cin >> n >> m;
for (int i=0; i<m; i++)
{
int x, y;
cin >> x >> y;
add_edge(x, y);
add_edge(y, x);
}
for (int i=1; i<=n; i++)
{
if (!DFN[i])
{
root = i;
tarjan(i);
}
}
int num = 0;
for (int i=1; i<=n; i++)
{
if (cut[i])
{
num++;
}
}
cout << num << endl;
for (int i=1; i<=n; i++)
{
if (cut[i])
{
cout << i << " ";
}
}
return 0;
}
例题
洛谷3388
比较简单就不打ac代码了。
























 582
582

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








