《算法导论》算法分析 5种渐近记号 Θ O o Ω ω

当输入规模足够大，使得运行时间只与增长量级有关时，需要研究算法的渐近效率。也就是，当输入规模无限增加时，在极限中，算法的运行时间如何随着输入规模的变大而增加。本文中所用插图来自《算法导论》。

不同的记号从不同的方面来刻画一个算法的运行效率。将插入排序的最坏运行时间刻画为下式：

f(n) = an²+bn+c，其中 a,b,c为常量，n为输入规模。下面针对插入排序最坏运行时间f(n) 来展开讨论
根据与 f(n) 的大小关系，可分为 “==”, “>=” “>” “<=” “<” 共5种记号，分别为 ：

• Θ（西塔） “==”
• O （大o） “>=”
• o（小欧）">"
• Ω（大欧米伽）"<="
• ω（小欧米伽）“<“

1、Θ（西塔）渐近紧确界

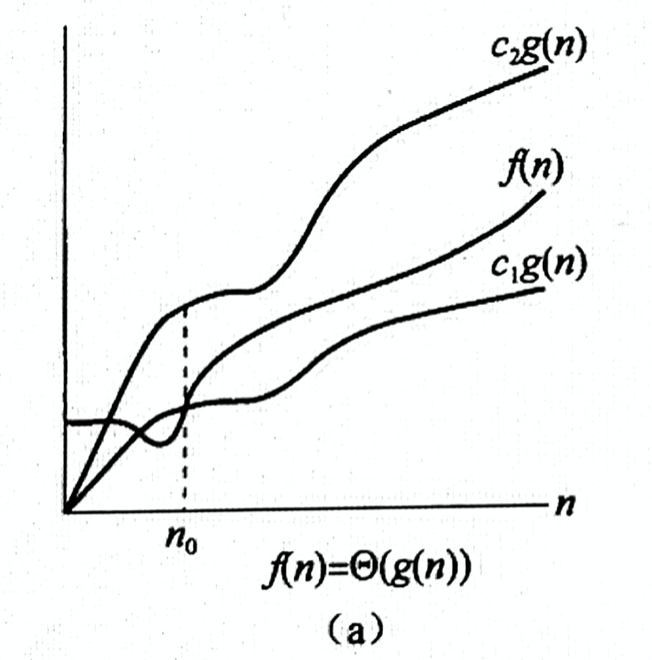
c₁，c₂为某个正常量，当n大于某一值时满足 0 <= c₁g(n) <= f(n) <= c₂g(n)，

插入排序最坏运行时间刻画为下式：f(n) = an²+bn+c

最坏运行时间：T(n) == Θ(g(n)) == Θ(n²)。一个渐近正函数的低阶项在确定渐近确界时可以被忽略，因为对很大的 n，它们是无足轻重的，当 n 较大时，高阶项的一个很小的部分足以支配所有的低阶项。

如下图所示：

2、O （大o）上界

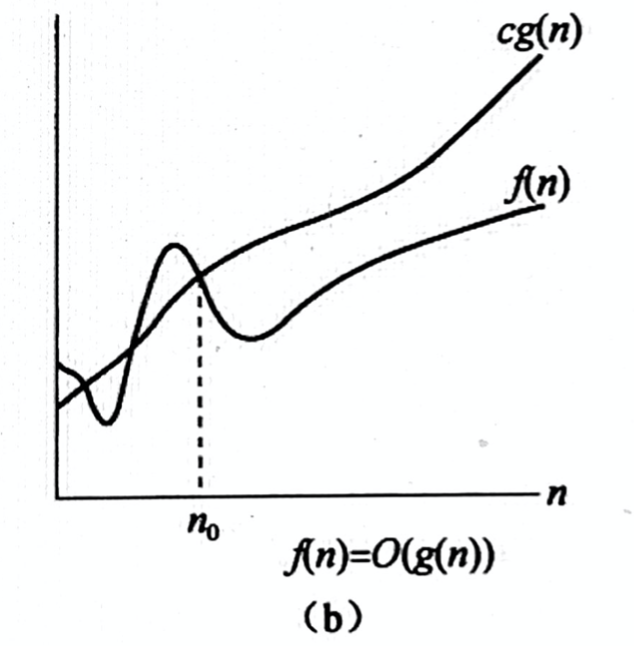
c为某个正常量，当n大于某一值时满足 cg(n) <= f(n)

插入排序最坏运行时间刻画为下式：f(n) = an²+bn+c

最坏运行时间 T(n) == O(g(n)) == O(n²)

如下图所示：

3、o（小欧）非渐近紧确的上界

任意正常量 c ，当 n 大于某w一值时，满足 **f(n)>cg(n) **

例如某个算法运行时间刻画为下式： f(n) = 2n

算法运行时间：T(n) == o(g(n)) == o(n²)

O 和 o 的区别：

f(n) = O(g(n))， 0 =< f(n) <= cg(n) 对某个大于 0 的常量 c 决定。

f(n) = o(g(n))， 0 =< f(n) <= cg(n) 对于所有大于 0 的常量 c成立。

4、Ω（大欧米伽）下界

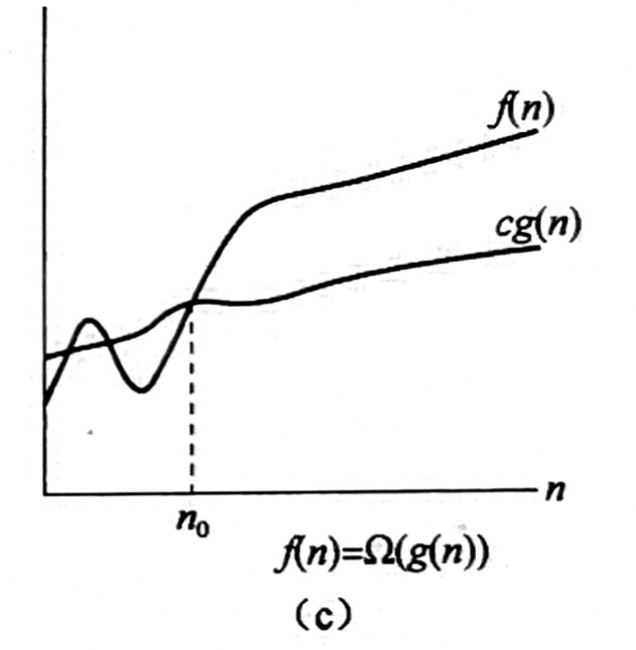
O 记号提供了一个函数的渐近上界，Ω记号提供了渐近下界。

c 为某个正常量，当 n 大于某个值时，满足 0< c(g(n)) < f(n)

算法运行时间：T(n) == o(g(n)) == o(n²)

5、ω（小欧米伽）非渐近紧确的下界

ω 记号 和 Ω 记号 的关系类似于 o 记号和 O 记号的关系。

对任意的正常量 c，当 n 大于某个值时，满足 0 < cg(n) < f(n)

算法运行时间：**T(n) == o(g(n))