Python实现Lasso回归

前言

最近刚还接触到Lasso，之前总是听到，但是从来没用过。他的数学原理不再赘述，主要以应用为主。

熟悉的图

我们通常在文章中看到的使用Lasso回归，通常会看到两个图：

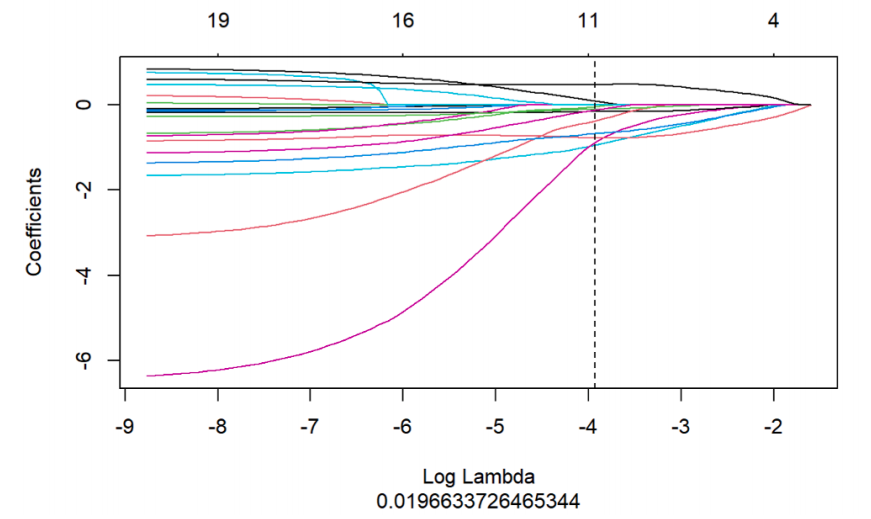
1. Lasso正则化路径图

这个图的意义：观察各个特征随着正则化强度（alpha）变化的过程
图中横坐标是alpha的log值，纵坐标是每个特征的标准化系数，每一条彩色的曲线表示一个特征系数的变化路径，垂直的虚线是最佳的正则化强度位置

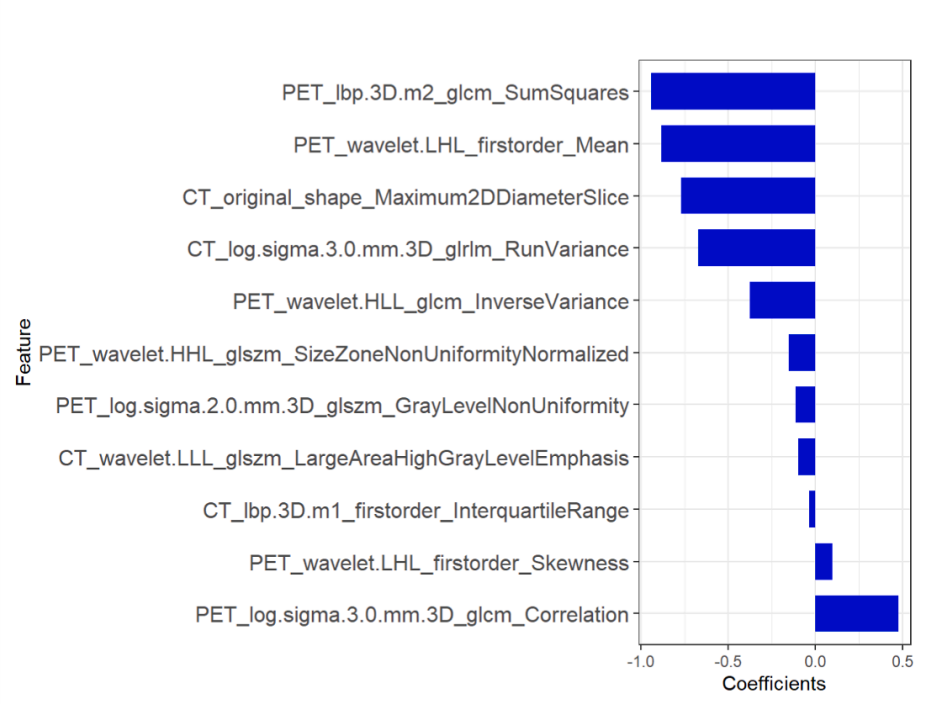
2. Lasso特征系数分布图

这个图的意义：从众多特征中，选择对模型最关键的几个特征，有点像SHAP可视化特征重要性
该图仅可视化了重要性较高的几个特征，可以将所有特征做可视化处理。（可以使用柱状图可视化重要特征，也可使用散点图将所有特征可视化处理，并标注重要特征）

python实现过程

1. Lasso正则化路径图

## 导入库
# coding=utf-8
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Lasso, LassoCV
from sklearn.linear_model import lasso_path
import warnings

warnings.filterwarnings('ignore')
# 配置全局样式
plt.style.use('seaborn-v0_8-darkgrid')
plt.rcParams['font.family'] = 'Microsoft YaHei'  # 中文字体支持
# 读取数据
url = rf'E:\Sci-Python\Characters.csv'
df = pd.read_csv(url,encoding='utf-8')
basic_info = ['Name', 'INFO_PatientName']
df = df.drop(basic_info, axis=1)
df = df.fillna(0)	# nan处理
x = df.drop('label', axis=1)  # becareful inplace= False
y = df['label']

# 数据标准化
scaler = StandardScaler()
x_scaled = scaler.fit_transform(x)

# 设置100个候选alpha值（对数均匀分布）
alpha_lasso = np.logspace(-4, 0, 100)
# 使用5折交叉验证Lasso
lasso_cv = LassoCV(alphas=alpha_lasso, cv=5, max_iter=1000, random_state=42)
lasso_cv.fit(x_scaled, y)
# 打印最佳alpha值
print(f"{character_kind}特征的最佳alpha值: {lasso_cv.alpha_:.6f}")

# 正则化路径（显示alpha如何影响特征系数）
# 计算正则化路径
alphas, coefs, _ = lasso_path(x_scaled, y, alphas=alpha_lasso)
# 绘制正则化路径
plt.figure(figsize=(12, 9))
for i in range(coefs.shape[0]):
    plt.plot(np.log10(alphas), coefs[i], label=x.columns[i])
plt.axvline(np.log10(lasso_cv.alpha_), color='k', linestyle='--',)
plt.title(f"Lasso Regularization Path",pad=20,fontsize=14)
plt.xlabel(f"Log10(alpha)\n\nOptimal alpha:{lasso_cv.alpha_:.6f}",fontsize=10)
plt.ylabel("Coefficient Value",fontsize=10)
plt.grid(alpha=0.5)
plt.tight_layout()
plt.savefig(f'E:\Sci-Python\Result\Figures\Lasso正则化路径',dpi=300)

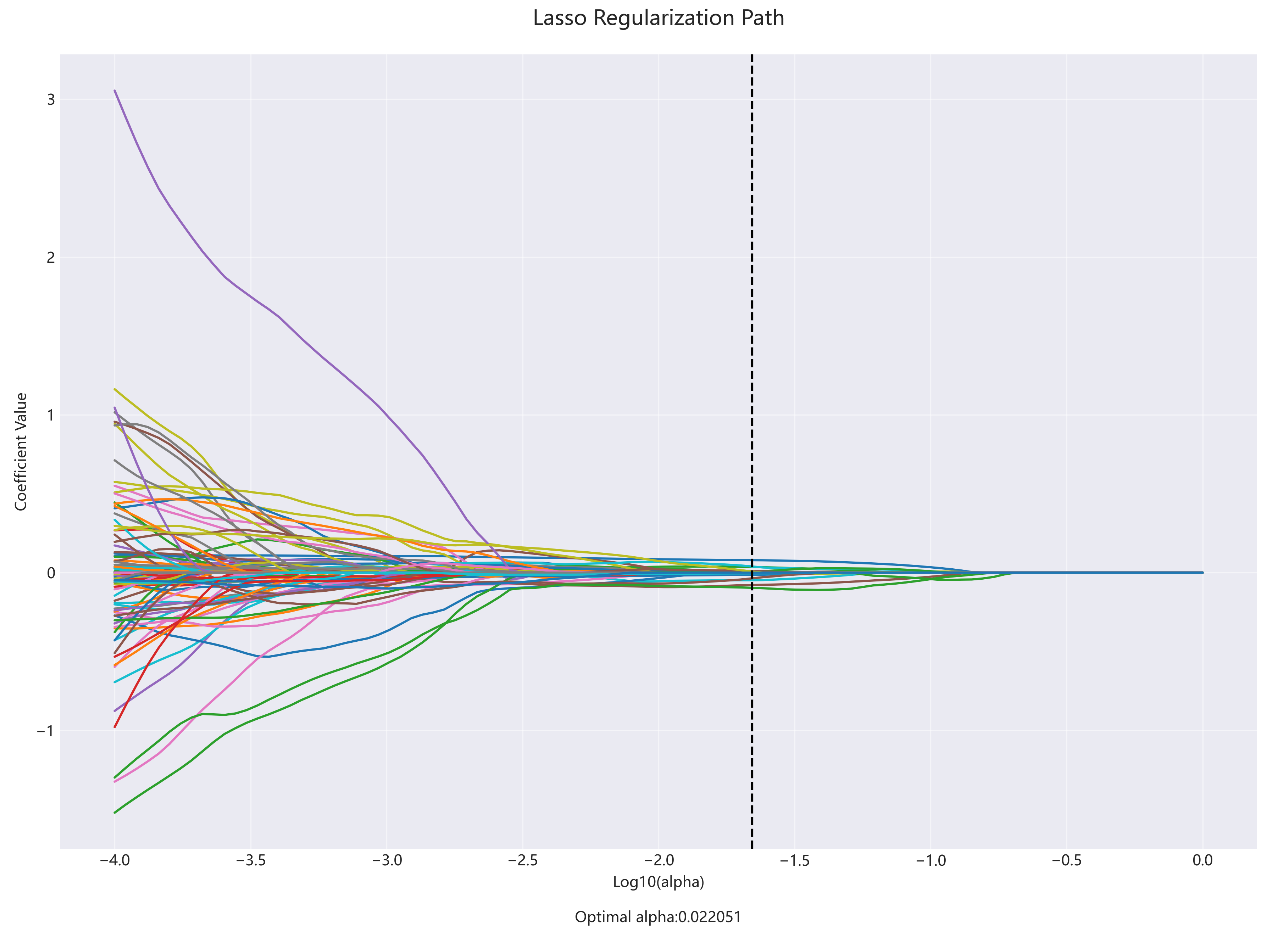
注：
1. Lasso无法处理表格中nan的数据，所以在进行Lasso回归之前一定要先检查数据中是否存在nan，如果存在先处理再进行后续

2. Lasso特征系数分布图（以散点图为例）

# coding=utf-8
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import Lasso, LassoCV
from sklearn.linear_model import lasso_path
import warnings

warnings.filterwarnings('ignore')
# 配置全局样式
plt.style.use('seaborn-v0_8-darkgrid')
plt.rcParams['font.family'] = 'Microsoft YaHei'  # 中文字体支持
# 读取数据
url = rf'E:\Sci-Python\Characters.csv'
df = pd.read_csv(url,encoding='utf-8')
basic_info = ['Name', 'INFO_PatientName']
df = df.drop(basic_info, axis=1)
df = df.fillna(0)	# nan处理
x = df.drop('label', axis=1)  # becareful inplace= False
y = df['label']

# 数据标准化
scaler = StandardScaler()
x_scaled = scaler.fit_transform(x)

# 设置100个候选alpha值（对数均匀分布）
alpha_lasso = np.logspace(-4, 0, 100)
# 使用5折交叉验证Lasso
lasso_cv = LassoCV(alphas=alpha_lasso, cv=5, max_iter=1000, random_state=42)
lasso_cv.fit(x_scaled, y)
# 打印最佳alpha值
print(f"{character_kind}特征的最佳alpha值: {lasso_cv.alpha_:.6f}")
# 使用最佳alpha训练Lasso模型
best_lasso = Lasso(alpha=lasso_cv.alpha_, max_iter=1000)
best_lasso.fit(x_scaled, y)

feature_names = x.columns
coef = best_lasso.coef_

# 5. 绘制特征系数分布图
plt.figure(figsize=(12, 9))
# 创建不同颜色的点：非零系数为红色，零系数为蓝色
colors = ['#f5a78c' if abs(c) > 1e-5 else '#59c1d6' for c in coef]      # 设置点的颜色
sizes = [abs(c)*10000 if abs(c) > 1e-5 else 5 for c in coef]            # 设置点的大小
edge = ['none' if abs(c) > 1e-5 else 'k' for c in coef]                 # 设置点的边缘
# 绘制所有特征系数的散点
plt.scatter(range(len(coef)), coef, c=colors, s=sizes, edgecolor=edge)
# 标注所有非零系数的特征
for i, (name, c) in enumerate(zip(feature_names, coef)):
    if abs(c) > 1e-5:  # 判断系数是否非零
        # 根据系数正负调整标注位置
        # vertical_offset = 0.13 if c > 0 else -0.13
        plt.annotate(name,  # 标注的名称
                    xy=(i, c),# 标注点的坐标
                    xytext=(0, 18 * np.sign(c)),  # 标注文字的坐标，因为下面选择的是offset，所以此处的设置是相对于上面的xy点的坐标进行的便宜，可以看出只进行了垂直偏移
                    textcoords='offset points',
                    ha='center',va='center',
                    fontsize=10,
                    bbox=dict(boxstyle='round,pad=0.2', fc='#f5a78c', alpha=0.25),
                    # arrowprops=dict(arrowstyle='->', color='black', alpha=0.7)
                     )
# 设置图表元素
plt.title('Lasso Feature Coefficients',pad=20, fontsize=14)
plt.xlabel('Feature Index', fontsize=10)
plt.ylabel('Coefficient Value', fontsize=10)
plt.grid(alpha=0.5)
plt.tight_layout()
plt.savefig(rf'E:\Sci-Python\Result\Figures\LassoFeatureCoefficients.png',dpi=300)

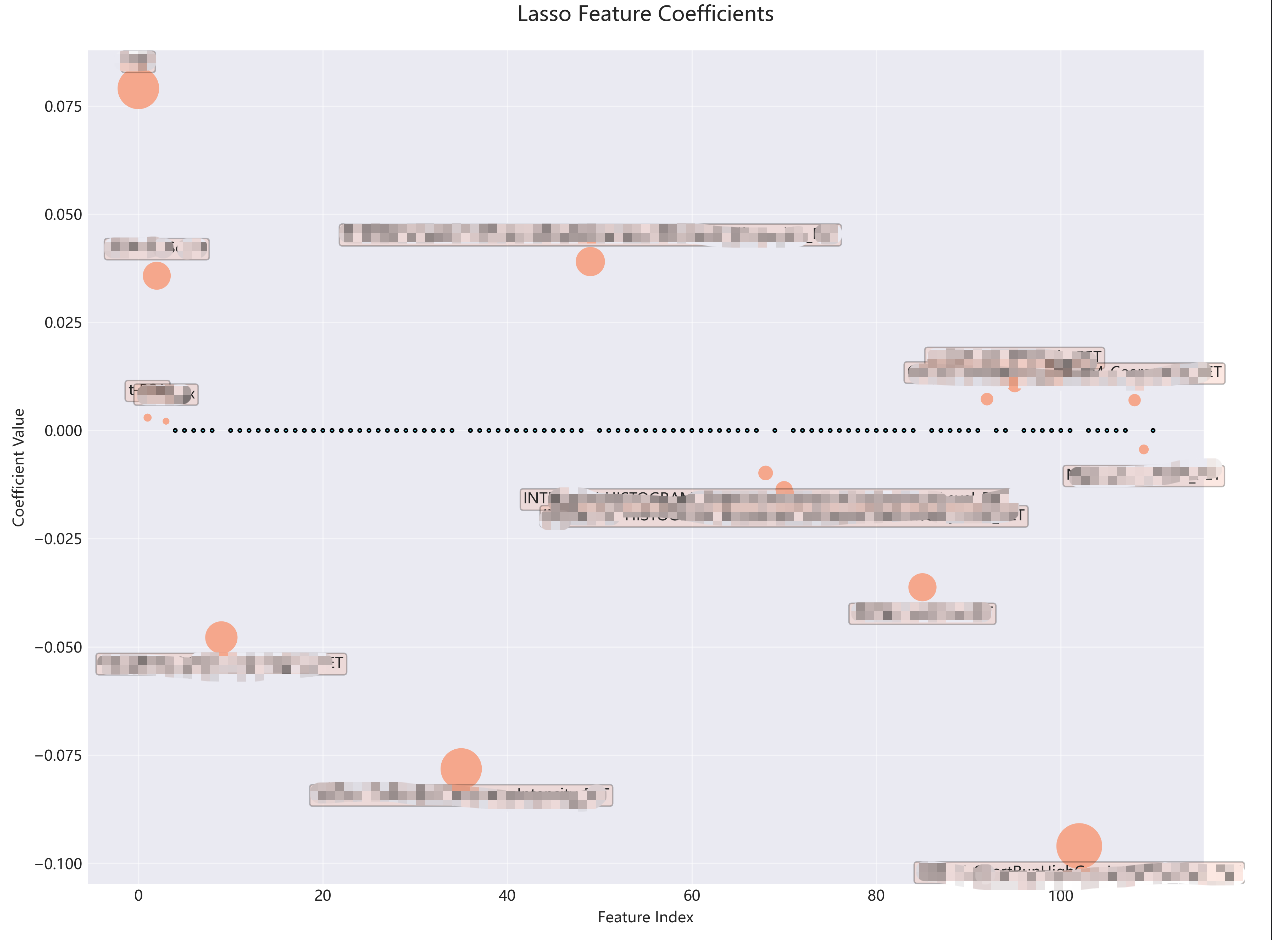
注
1. 马赛克的地方是重要特征的名称
2. 绘制scatter散点图的颜色，点的大小，还有点的样式都可以改变
后续还会分享一些基本的小技能。期待着吧~