前言
切比雪夫是俄国超级有名的,土生土长的数学家,其比较出名的贡献有:切比雪夫多项式和切比雪夫大数定律。本文说切比雪夫多项式。
参考视频:切比雪夫多项式。
多项式函数

而且一般说某一个函数是多项式函数的时候,我们还会说其是多少次的,比如一次函数就是1次。
切比雪夫多项式
其表达式如下:

有人一脸懵逼,函数中有cos的东西,竟然最终会是x的多项式?这其实一点也不奇怪,为什么呢?个人觉得是因为x的定义域很古怪,从而这和三角函数会有千丝万缕的关系。你看下面的例子, n = 2 , x = c o s θ n=2,x=cos\theta n=2,x=cosθ,不看中间那个,即左边等于右边,右边就是 2 x 2 − 1 2x^2-1 2x2−1,左边就是 c o s 2 a r c c o s x cos2arccosx cos2arccosx,妙吧。

现在,我们要证明,对于任意n,右边都会是
c
o
s
θ
cos\theta
cosθ的多项式。

温馨提示,左边那个式子肯定是有实部和虚部的,我们要找到的就是会被
i
2
=
−
1
i^2=-1
i2=−1抵消的那些实部,从而我们可以发现,左边实部=
c
o
s
θ
cos\theta
cosθ的多项式=右边实部=
c
o
s
n
θ
cosn\theta
cosnθ。
我们继续证明一个小东西,即不但
c
o
s
n
θ
cosn\theta
cosnθ是
c
o
s
θ
cos\theta
cosθ的n次多项式,而且系数是
2
n
−
1
2^{n-1}
2n−1。
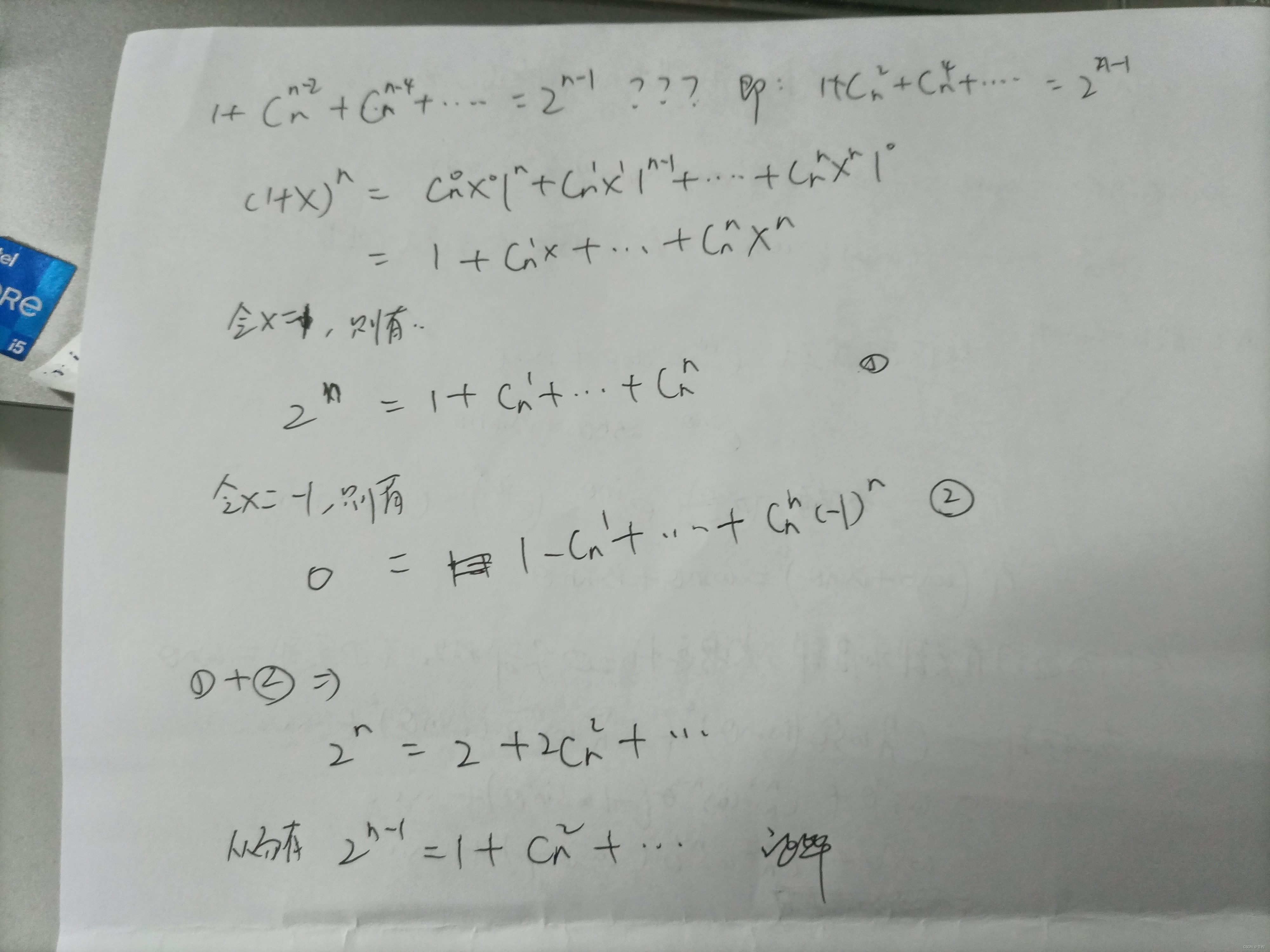
这就证明完了。
性质
递推式
我们知道,当n取不同数的时候,得到不同次数的切比雪夫多项式。但是由于三角函数性质贼多,所以相邻的3个切比雪夫多项式存在如下关系:
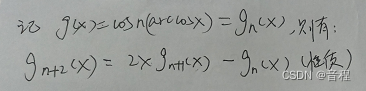
完整证明如下,归根到底是三角函数的性质多


























 1135
1135

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










