【论文阅读】Contract and Lyapunov Optimization-Based Load Scheduling and Energy Management for UAV Chargin

论文基本信息

《Contract and Lyapunov Optimization-Based Load Scheduling and Energy Management for UAV Charging Stations》
《基于契约和Lyapunov优化的无人机充电站负荷调度和能量管理》
IEEE TRANSACTIONS ON GREEN COMMUNICATIONS AND NETWORKING, VOL. 5, NO. 3, SEPTEMBER 2021

摘要

如今，大量的民用无人机（uav）越来越多地应用于我们的日常应用中。然而，由于其资源有限，有许多种类的无人机需要提高其续航能力。为了使无人机高效运行，有必要安排有充电要求的无人机。本文采用传统充电站基础上的可再生能源生产和存储设备，尽可能减少配电网的购电量。提出了一种基于李雅普诺夫优化算法的在线无人机充电调度算法和充电站能量管理算法。同时，利用契约理论设计了信息不对称情况下的最优充电策略。因此，可以最大限度地利用当地的可再生能源，并可以降低电力购买成本。通过激励系统，用户可以在低高峰时间自发充电，避免了电网过载和高能源成本的风险。仿真结果表明，该算法可以提高充电站操作人员的工作效率，使用户可以避免在高峰时间进行充电，且仅利用实时信息对无人机进行调度。与其他算法相比，该方案可以在确保充电站长期运行的同时，为运营商带来良好的收入。

1.引言

无人驾驶飞行器（uav）是近年来发展非常快的技术。此外，随着5G的快速发展和无人机相关法规[1]、[2]、[3]的不断改进，越来越多的无人机被部署在不同的领域和应用[4]。单架无人机的效率较低，因此无人机逐渐倾向于聚集。在现代控制技术下，集群无人机可以有序地执行相同的目标。随着控制、通信、智能调度等技术的快速发展，集群无人机不再仅用于军事行动。在农业领域，集群无人机可以喷洒农药，并调查不同的农业目的，如保险。在公用事业领域，集群无人机可用于电力检测、火灾探测等方面。此外，集群无人机还广泛应用于物流、运输、救灾、艺术性能等领域。对于集群无人机，高效充电对于提高其生存能力和延长其[5]寿命至关重要。

为了使无人机的充电更加方便，可以在许多地方建立充电站，但这些充电站没有合理规划的充电活动会对电网[6]、[7]产生不利影响，不能及时为无人机提供充电服务。在没有约束的情况下，无人机的充电行为是自发的和随机的，这将进一步加剧峰谷差和功率波动。在某些情况下，它甚至会超过电网的可调范围，从而干扰电网的稳定运行。因此，需要制定相关的策略来调整无人机[8]的充电时间。另一方面，充电站也引入了可再生能源，以减少从电网购买的电量。这不仅可以降低电力成本，而且有利于减峰负荷，从而有效地提高了电力系统[9]的安全性和经济性能。然而，可再生能源是间歇性的和不确定性的，这些因素可能会在实际给无人机充电时带来许多挑战。这个大量的充电需求不仅会影响电网，还会给运营商带来严峻的挑战。为了保持长期的服务，充电站需要满足自身的盈利能力，保持充电站的稳定性，从而使到达的无人机能够及时充电。一般调度需要当前和未来无人机的充电信息，这增加了在线调度的难度，容易导致信息泄漏[10]、[11]。因此，运营商需要提供一种在线调度策略，既能满足无人机的充电要求，又能优化充电站的运行成本。

在无人机充电的有序调度方面，[12]和[13]已经进行了相关研究，考虑无人机为移动负荷，并制定了相关规定。[14]的研究设计了一种基于拍卖的机制来控制多无人机设置下的充电时间表。在[15]中，Hassija等人提出了一种调度算法，针对具有优化临界性和任务期限约束的无人机。Lin等[16]提出了一种无人机的充电再分配机制，该机制可以通过提高充电能量、降低移动成本和传感成本来提高能源效率。虽然这些算法已经实现了充电无人机的有序调度，但它们并没有考虑到运营商利润的增长。

为了进一步提高运营商的利润，降低与电网连接相关的风险，运营商可以通过协调所提供的服务和差异定价，制定良好的激励计划，并指导无人机在低高峰时间[17]自动充电。在之前的工作中，[18]和[19]发展了一个在激励机制方面非常合适的契约理论，特别是在信息不完整的情况下（例如，操作者只能知道用户偏好的分布，而不知道用户的具体选择）。例如，Zhou等人提出了一种基于凸凹过程的服务器招聘契约优化算法，旨在使具有非对称信息[20]的操作员的期望效用最大化。在[21]中，提出了一种契约理论的方法来解决蜂窝网络中D2D通信的激励问题，从而有效地鼓励用户的参与，并比其他机制增加蜂窝网络的容量。在[22]的研究中，Zhou等人提出了一种有效的激励机制，鼓励服务器利用契约理论共享其剩余的计算资源。基于合同理论，纳米川等[23]提出了现场电价策略，以确保电网安全运行。契约理论在[24]管理领域也有许多应用。Gao等人[25]通过优化合同的设计，将能源费率与服务需求相匹配，使运营商的利润最大化。Zhou等[26]研究了在信息不完整的情况下，每个消费者可以根据自己的类型（即私人信息）选择自己的数据计划。上述研究在考虑增加运营商利润的同时，没有考虑收费调度的问题。

除了适当的激励计划外，可再生能源还可以减少用电量，减少充电站的电量。在[27]的研究中，Leithon等人提出了一种由可再生能源（RE）驱动的物联网（IoT）节点的任务调度策略。尽管可再生能源存在随机性和不确定性，但可再生能源在充电方面也有实际应用，如巴塞罗那的风力充电站和韦斯特波特[28]市中心的带屋顶太阳能充电板的充电站。针对可再生能源发电的随机问题，李雅普诺夫优化技术[29]已应用于智能电网[30]、[31]、[32]中能源系统的相关研究。在[33]中，研究人员证明了李亚普诺夫优化技术可以解决可再生能源供应的不确定性。

针对上述文献在无人机调度中的局限性，本文采用李亚普诺夫漂移优化理论，处理在线调度和可再生能源管理问题。该理论在排队网络中广泛应用于排队网络，可以在保证排队网络稳定性的同时，优化平均功率、吞吐量等性能指标。在以往的工作中，李亚普诺夫优化也被应用于充电调度。[34]的研究提出了一种基于事件触发的在线能量管理算法。采用李雅普诺夫优化方法调度家庭可控负荷。在[35]中，Zhou等人采用李亚普诺夫优化方法研究了充电过程，提高了充电服务质量。此外，与之前提出的无人机充电调度相比，本文提出的调度方法可以仅基于当前信息进行决策，而不预测相关变量，减少了不必要的计算。本文的主要贡献如下。

1. 设计了一种基于合同的激励方案，在调整运营利润最大化的同时，调整无人机的充电时间，以降低峰值。在信息不完整的情况下，可以得到最优的费率-价格契约。
2. 采用李雅普诺夫优化技术处理可再生能源管理和无人机调度，在保证充电队列稳定性的基础上，可以进一步获得更高的运营利润。
3. 仿真结果证实了该合同提高营业利润的可行性。通过无人机的合理调度，实现可再生能源的充分利用，保证充电队列的稳定性。与其他方案相比，证明了该方案的优越性。

本文的其余部分的安排如下。在第二节中介绍了该系统模型。在第三节中，给出了问题的公式。该问题的分解和求解方法见第四节。在第五节中，我们分析了仿真结果和算法的性能。最后，在第六节中得出了结论。本文给出的主要数学符号见表一。

2.系统模型

我们将讨论在图1所示的情况下，无人机的充电调度问题。该图首先展示了集群无人机运行的场景，如农林检测、数据收集、环境监测等。为了保证无人机能够及时充电，将在无人机作业区建立大量的充电站。不同类型的无人机在时间段t上上传自己的充电需求和期望价格，通过比较得到最佳充电价格和充电率，然后由运营商将其分配到合适的充电桩进行充电。本节主要介绍了充电网络系统的模型，该系统由充电桩、与充电站相连的储能装置、有充电要求的无人机的随机到达组成。

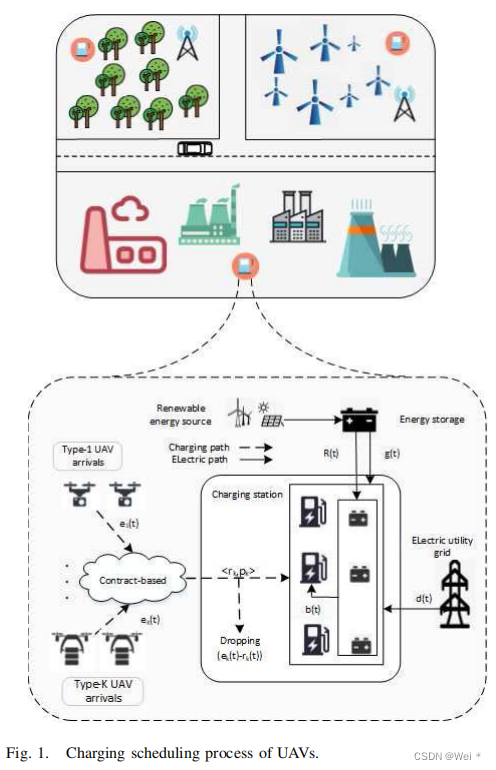
A. Distribution Network and Charging Station Model

在本节中，让i∈{1,2，…，N }表示第i个充电桩，其中N为充电桩总数，k∈{1,2，…，K}表示第k个无人机，其中K是中央管理系统可以接收的最大用户数。第k架无人机的能量需求被写为ek (t)∈[0，emax]。

为尽量减少充电站与电网连接的负面影响，每个电站都配备了可再生能源发电机。然而，可再生能源是不可预测的和间歇性的，所以在本节中，每个充电站都携带可充电电池来存储可再生能源。可再生能源相关设备的前期投入成本是一个常数，与本文的优化无关，因此可以忽略。设gi (t)∈[0，gmax]为生产速率第i个充电堆的新能源。新能源首先被提供给无人机进行充电，其余的则被充电进入电池。设Bi (t)∈[0，Bmax]为第i个充电桩的当前电池能级。

设ri (t)∈[0、ri，max]为第i个充电桩的充电速率。在每个时间段内充电进入无人机的能量首先由可再生能源直接提供。如果可再生能源没有用完，它将被充满电池。设Ri (t)为每个时间段充电堆电池的新能源，则Ri (t)∈[0，min{Ri，max，(gi(t)−ri(t)+}]，其中(x) +ˆ=max{0，x}。如果充电率高于可再生能源产生率，则电池不充电，而（ri (t)−gi (t)）+为电网或电池提供的能量。假设di (t)∈[0，dmax]是第i个充电桩从配电网购买的能量，bi (t)是第i个电池提供给无人机的能量，其中bi (t)∈[0、Bi (t)]、bi (t)∈（0、Bi、max]。满足了无人机充电的能量平衡

式中，gi (t)为第i充电堆新能源的产生率，（ri (t)−gi (t)）+为电网或电池提供的能量，bi (t)为第i电池提供给无人机的能量。（d是充电桩需要向电网购买的，r是充给AUV的，g是充电桩自己产的，b是用充电桩之前存储的给无人机充的电）

由于电价是实时的，所以用c (t)表示运营商在时间段t内购买电力的单位成本，c (t)的范围为[Cmin，Cmax]。

B. UAVs’ Charging Request and Guidance Model

为了引导无人机，需要建立充电桩与无人机之间的连接。无人机上传自己的充电请求，操作员通过计算得到合理的决策，并将引导计划发送给无人机。Wk，i (t)∈{0,1}描述了第k架无人机与第i架充电桩之间的关系。Wk，i (t)=1表示第k个无人机指向第i个充电桩，否则两者之间没有相关性。根据实际情况，在同一时间段t内，无人机必须且只能分配到一个充电桩上，即：

除了无人机的能量需求外，还有实际的充电率。根据无人机的指导，我们有

式中，rk (t)为无人机k的充电率。

下面，根据合同设计根据特定的价格匹配不同的收费费率。根据已知的收费率，可以得到相应的收费价格。由于收费率的不同，每个收费桩都有不同的利润。所以设pi (t)为收费桩的收入，即，

式中，pk (t)为无人机k的充电价格。

C. User Model

对于无人机用户来说，人们总是渴望快速充电和相应的低价格。但事实是，快速收费肯定会花费更多的钱，所以用户在收费时必须在价格和费率之间进行权衡。为了量化价格和费率之间的关系，我们引入了θk来表示用户k对收费率[16]的偏好类型。每个θk对应于一组关联策略<rk (t)，pk (t)>，k∈{1,2，…，K}。这意味着，如果θk类型的收费率为rk (t)，则应支付给运营商的费用为pk (t)。

为了使用户更好地配合方案，应在相关策略中加入用户的条件激励。也就是话说，用户的条件激励可以通过他们对收费率和差价的偏好来实现。简单地说，这意味着喜欢低价的用户将在低高峰时段收费，而想要在高峰时段快速收费的用户将支付更多的费用。

不同的收费率会带来不同的用户体验。因此，根据用户对收费率的偏好，θ表示为用户满意度每增加一个单位费率的增加。当θ越大时，用户对满意度的需求就越大。假设用户满意度与收费率成正比。由于对数效用函数可以更好地表示用户的分布比例而没有较大的偏差，因此用户k的满意度函数可以定义为随收费率单调增加的函数，即：

D. Battery and Charging Demand Queue Model

对于第i个充电桩，电池的能量态Bi (t)应满足以下式

其中，bi (t)表示通过充电堆i从电池中提取的能量，Ri (t)表示可再生能源被充电到电池中的速率。

你对电池的能量也有限制，这个限制是

这个公式表明，电池可以提供的能量和电池的容量是有限制的，后续的算法将满足这一约束。

为了保持充电站的持续工作，运营商需要制定适当的调度方案，以保持无人机的充电需求不受积压的影响。无人机的请求时刻都是随机的，因此引入一个虚拟需求队列来描述充电请求和能量供应之间的关系。将时间段t中对充电桩i的需求记为Qi (t)，那么我们可以得到以下队列

式中，ek (t)表示用户k的能量需求，${\sum }_{k=1}^K{W}_{k,i}(t)e_k(t)$为到达充电桩i的能量需求，ri (t)为充电桩i的实际充电率。该队列的稳定性的定义如下。（公式（8）的意思是——减去t完成的，加上t新来的需求）

定义1：一个类似于Qi（t + 1）= max{Qi (t)−m (t)，0} + a (t)的离散时间队列，如果满足，则是强稳定的

其中E{Q(ι)}表示队列Q(ι)的期望。

在Neely的工作[36]中，如果队列是强稳定的，那么系统必须是稳定的。另外，强稳定队列必须满足系统处理能力m (t)和随机到达能力a (t)的稳定速率，即：

3. PROBLEM FORMULATION

本文的目标是最大化运营商的时间平均利润，满足电池和稳定的队列需求的约束。

根据上面的(5)项，我们可以得到用户的效用函数

式中，为用户满意度与价格之间的比例系数。在正常情况下，取=1，用(5)替换到（11）得到

从用户的角度来看，只有当相关性策略满足以下两个约束条件时，用户的动机才能得到保证。这两个约束在激励机制设计[18]，[24]。

定义2 (IR：个人合理性）：用户的效用必须是非负的，即，

定义3（IC：激励兼容性）：与其他策略相比，用户所选择的相关性策略必须是最合适、最有效的，即：

运营商的利润是用户的费用减去运营商从电网购买电力的费用，即：

那么运营商平均利润为

因此，经营者的利润最大化可以总结如下。

问题P1的目标是使运营商的利益最大化。在问题P1中，电池的充放电被及时耦合。也就是说，电池当前的充放电状态将对未来产生影响。这将增加在线调度的计算量，并在实践中得到广泛的应用。因此，为了放宽Bi (t)的稳定性约束，可以将问题P1放宽为

问题P2根据公式（10）放宽了队列Bi (t)的约束，使电池的充放电不再受过去时间的限制。假设问题P1的最优解是P1∗，那么P1∗必须满足P2的约束。虽然P2的解不是最好的，但它也可以解决问题P1。可行解与最优解之间的差异将在定理1中显示出来。让我们先解决问题P2。

4.PROBLEM DECOMPOSITION AND SOLUTION

A. Simplification and Decomposition of the Problem

解决问题P2存在很大的困难，例如一次充电桩的充电完成程度会影响下一次的充电进度。此外，关于收费的信息是随机的。为了实现在线实时调度，需要将问题进行简化，并将其分为几个子问题来解决。

为了满足关于Bi (t)的约束(7)，并确保电池提供给无人机的充电功率不超过自己的极限，有必要将Bi (t)转换为另一种形式，类似于[22]，Bi(t)的转换版本设置为$H_i(t)=B_i(t)-V{C}_{max}-r_{i,max}$，其中V是稍后介绍的控制参数。因此我们有

一个新的虚拟队列被构造为Θ(t) =（Q1(t)，…，QN (t)、H1(t)，…，HN (t)）。

分别定义李雅普诺夫函数和李雅普诺夫漂移如下

将运营商的利润合并为利亚普诺夫漂移器，以保持网络的稳定，使运营商的利润最大化。因此，所考虑的问题可以转化为贪婪地最小化漂移加惩罚，即：

其中，−E{Upro (t)|Θ(t)}为惩罚项，V为控制参数，用于衡量操作员的利润和队列的稳定性。

由于上面的方程包含了对队列Qi (t)和Hi (t)的稳定性的约束，因此可以将问题P2更改为

在问题P3中，V是一个可调参数，以平衡运营商的收入和充电系统的稳定性。它从公式（21）可以看出，问题P3包含了属于时隙t + 1的变量，这使得直接解决问题变得困难。所以我们需要在（22）中找到一个漂移加惩罚的上界。

通过(8)和（19）两边的平方，我们可以得到

此外，我们还可以得到

然后通过对（26）和（27）的求和，我们得到了

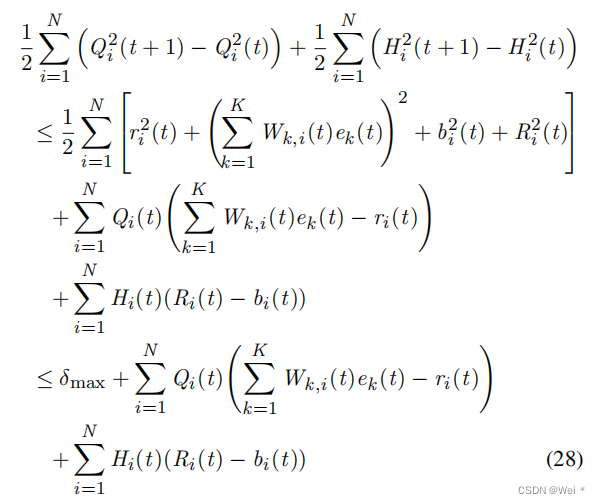
其中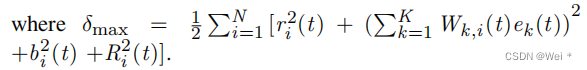

通过将问题P3的（28）、（15）和约束(1)和(4)替换入（22），我们可以得到

因此，最小化（22）中的漂移加惩罚函数可以转换为最小化公式（29）的右侧。

定理1：设置E{L[Θ(0)]} <∞，并定义U∗来表示期望的最优解。假设存在有界正实数V、B、γ，因此对于任意时间段t的队列积压，李亚普诺夫漂移加惩罚函数满足

我们可以有

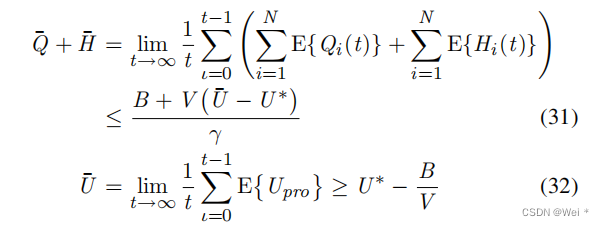
证明：见附录A.1。根据（30），P3可以简化为

问题P4可以转化为两个子问题P5和P6，即合同设计问题和充电桩选择问题。问题P5（即公式（33）中的第三项）考虑设计一种收费策略，以使运营商的利润最大化。问题P6（即公式（33）中的第一项和第二项）描述了无人机的调度问题，以维持充电站的长期运行和平衡电池能量的问题。问题P6可以进一步细分为关于无人机调度问题的P6(a)和关于能源管理问题的P6(b)。

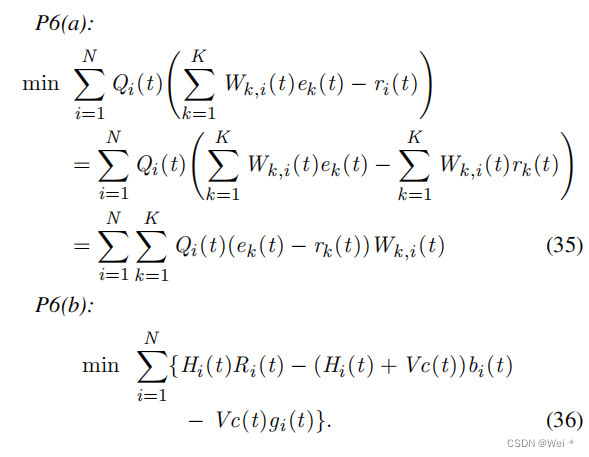
B. Solving Sub-Problems

本节将详细介绍解决P5和P6的过程。P6的解与P5的结果密切相关，具体关系如下所示。

5.仿真结果 SIMULATION AND PERFORMANCE ANALYSIS

6.总结

提出了一种基于李雅普诺夫优化的无人机充电方案，该方案既能保证用户主动参与调度，又能提高运营商的收入，使充电站长期使用不拥堵。每个充电站都有可再生的生产和存储设备，以减少购买成本的电力。利用李雅普诺夫优化和合同理论为无人机提供在线充电指导，同时可以充分利用各充电桩的现有能量。该算法不需要过去的信息，大大减少了信息收集的差异和不必要的计算。该算法为无人机提供实时充电指导，并为低效率站点制定能源管理计划。仿真结果表明，该算法能在提高运营商收入的同时，满足无人机的充电需求。此外，该算法时间复杂度低，计算资源较少。

补充

无人机随机到达去充电桩充电，要维持充电桩的稳定运行，同时最大化充电桩运行商的利益。（这个角度考虑还蛮有意思的）