本文分享了作者考软件设计师的经验，强调了C语言、数据结构和设计模式的重要性。文章介绍了考试结构，上午题侧重数据结构、UML流程图、设计模式和软件开发模型，下午题涉及数据库、算法题和设计模式题。作者推荐了学习资源，如MOOC课程，并提倡通过真题练习、记录笔记和归总知识点来备考。
软设知识点记录
以下是我个人考软件设计师的一些经验，本人一共考了两次软件设计师，第一次下午题查三分，第二次成绩还没出，虽然没什么悬念，这里分享一下我考软件设计师的一些经验分享
需要知识储备
- C语言
- Java或C++
- 数据结构
- 没了
考试结构
- 上午题
- 数据结构知识
- uml流程图
- 设计模式
- 软件开发模型
- 杂七杂八
- 下午题
- 数据库（类似阅读理解，找不同）
- 一到三题都是阅读理解，答案基本在文中都能找出来
- 算法题
- 设计模式题
学习方法
学习方法有很多种，但是绝对不推荐买软官网卖的书
本人使用的方法
-
直接真题，哪题不懂搜哪题，记录笔记，归纳知识点，因为考点比较杂，记录到一定时间时要对笔记进行归总，哪些笔记属于同一个知识点，到时复习时又个联想记录方便，也有助于记忆
-
完善基础
- C语言
- 最好先学个C，不想学C，想速成考证的，也不是不行，就算下午题第四题不写，一分不拿，光靠其他几题也是可能通过的，不过会增加之后的学习难度，和对数据结构知识理解的难度作为基础学习对于往后学习也有帮助
- C学习资源推荐MOOC中国大学，选个国家精品看就行，学到 结构类型、指针、链表差不多够用了
- 中国大学MOOC 程序设计入门——C语言 翁恺
- 数据结构
- 大部分数据机构的课程都是使用C语言来讲解的，C有基础后，数据结构就是一种思想，虽然软件设计师考的比较浅，但是如果想进行往后的学习，敲一敲代码还是比较有必要的，整门课程学习
- 数据结构资源推荐 MOOC ，数据结构 浙江大学的也是国家精品
- 中国大学MOOC 数据结构 浙江大学
- Java
- Java是下午题最好拿分的，只要五个空，拿满就15分，性价比最高的题目，第六题要结合设计模式一同理解作答，光靠找技巧不容易哪满分，找技巧得分应该不会超过9分，要拿满只要学完Java基础后多理解一个设计模式就行
- 资源推荐MOOC Java核型技术初级看到38p差不多了
- 设计模式，菜鸟教程，理解为主，从整体看，从结构看到细节，到数据流走向
- 中国大学MOOC Java核心技术 浙江大学
- 菜鸟教程 设计模式
- C语言
-
使用51CTO小程序刷题，这个是比较实用的，直接刷题，哪题不懂，学哪题，还可以加入学习群一起学习，不理解的发到群上，虽然基本也没什么用，但是群上吹吹水放松一下还是很不错的
-
买课，针对考试的课程有很多，我买了51CTO的课，选一个便宜的，上午100的视频，下午99的视频，就算零基础，有充分的方法，少走弯路一次过软件设计师完全不是问题，不推荐买几千的课程，没必要
我还记录了很多很多笔记在OneNote，都是个人自然语言描述有需要可以联系我
以下都是我考前复习的一些随笔
数据结构
- 挂在右子树上
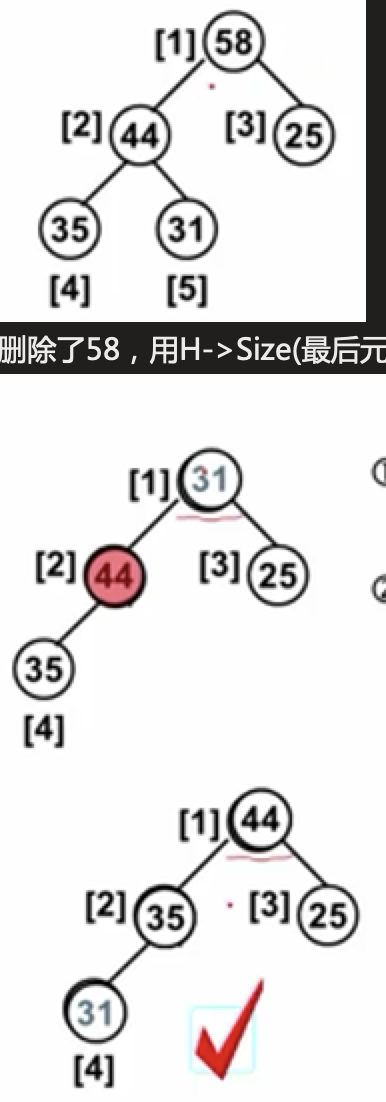
- 最小堆，哈夫曼树，霍夫曼树，最优二叉树
- 提高编码效率
- 图的遍历；
- DFS深度优先遍历
- BFS广度优先遍历
杂项记录
- 计算执行时间，取指，分析，执行，100条
- 顺序方式，（取指+分析+执行）*100
- 流水线方式（取指+分析+执行）*1+（分析+执行） * 99
- 系统总线
- 地址
- 数据
- 控制
- 系统初始化过程，按照自底向上可分为
- 片级初始化
- 板级初始化
- 系统级初始化
- 以软件初始化为主
- 主要进行操作系统初始化
- 加载设备驱动
- 建立内存
- 加载初始化其他软件模块
- 创建程序应用环境，将控制权交给应用程序
- 嵌入式操作系统
- 微型化
- 可定制
- 实时性
- 可靠性
- 易移植性
动态规划：
01背包问题：
- 要求装尽价值尽可能多的物品，求最大价值
- 在背包中和不在背包中，0和1
- 数据流图平衡：任何一个数据流子图必须与它上一层父图的某个加工对应，二者的输入数据流和输出数据流必须保持一致，此即父图与子图的平衡，父图与子图平衡中，数据流的数目和名称可以完全相同，也可以在数目上不相等，但是借助数据字典中数据流描述，确定父图中的数据流是由子图中几个数据流合并而成的，也即子图是对父图中加工和数据流进行分解
结构化分析一般包括以下工具：
- 数据流图（Data Flow Diagram ）
- 数据字典（Data Dictionary）
- 结构化语言
- 判定表
- 判定🌲
用例之间的关系：
- 包含
- 扩展
- 泛化
命名冲突：
- 两个属性名相同，但是分别属于两个不同的关系模式，可以通过“关系名.属性名“区别。
活动图和状态图的区别：
-
活动图主要描述行为的动作
-
状态图主要描述行为的结果
第四题
01背包问题
-
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-boJlKirk-1604904857994)(…/…/…/Library/Application Support/typora-user-images/image-20201030181720107.png)]
-
C是一个二维数组保存最优的装包方案
-
递归式
- i=0 没有物品， T=0 背包容量为零的时候，价值为0
- T<w[i]，如果第i个物品的重量比背包容量大了，第 i 件物品无法装入背包，所以，当前的最大价值就是i-1个物品时的最大价值
- i>0 T>=w[i] 还有物品，并且 背包容量能装下第i个物品，装入物品时背包容量会减少，
- c[i-1] [ T-w[i] ]
- 当前物品是w[i]，装入后是T-w[i]
- 对应的前 i-1 个物品的价值加上第i个物品的价值的总和
- 对比c[i-1] [T] 不装这个物品的总和进行对比，选出最大值
- c[i-1] [ T-w[i] ]
-
c[ i ] [ j ] 表示i个物品在背包容量为 j 的情况下最优装包方案能获得的最大价值
-
采用大方法是，动态规划设计方法，动态规划和分治法大差别就是会保存中间结果
-
采用大是自底向上的方式，要求出第六个物品的最优解需要求出前五个物品的最优解
代码实现
-
#include<stdio.h> #include<math.h> #define N 6 #define maxT 1000 int c[N][maxT]={ 0}; //c[i][j]：表示前i个物品在背包容量为j的情况下最优装包方案所能获得的最大价值 int Max_Value(int v[N],int w[N],int i,int j){ int temp; if (c[i][j] != -1) { //初始化时把值全部设置为了-1，如果不是-1，说明已经对这个值进行了更改，将保存的值返回，返回当前价值 return c[i][j]; } if (i == 0 || j == 0) { c[i][j] = 0; //没有物品 和 背包容量为 0 的时候，对应的第i件物品的，重量为j的物品，价值为0 //当c[0][j]的值一定为0， //要考虑在前 i 件物品中拿取，就要考虑i-1件物品中拿取的最优情况 ，价值才有可能是最大的，前面拿取的都不是最大的，后面拿取的自然也不是最优的，都需要是最优的事，依次往前推，保证每次拿取的都是最优的，这是递归的思想，在求解 i 时，先求解 i-1，求解 i-1 时先求解 i-1-1 。。。。 //当递推到 i 件时候，要考虑物品时拿还是不拿，如何收益才是最大的 //拿的了和拿不了，j<w[i]是拿不了的 //能拿的情况要考虑拿了之后收益是否更大，拿这件物品需要花费的w[i],除去这w[i] 的子问题应该是c[i-1][j-w[i]]，j是会变化的，j是原来的可用空间，拿取之后克可用空间变少，j减去w[i]加上第i个物品的价值，对比不放入第i个物品的价值，选个最大的价值返回 } else { //在程序实现时直接不用考虑放不进去的情况 c[i][j] = Max_Value(v, w, i - 1, j); // if(__(2)__){ if (j >= w[i]) { //可用空间大于物品重量 // temp = __(3)__; temp = Max_Value(v, w, i - 1, j - w[i]) + v[i]; //选择放还是不放 if (c[i][j] < temp) { //新加入的值比原有的价值大，进行更新 // __(4)__; c[i][j] = temp; } } } return c[i
最低0.47元/天 解锁文章
扫一扫
703
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
