文章目录
1. 图相关概念
-
图可以用
(V,E)来表示,V表示顶点的集合,E表示边的集合 -
图分为有向图和无向图
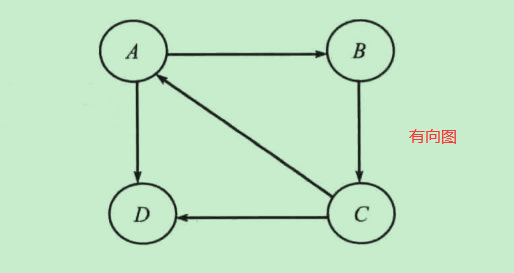
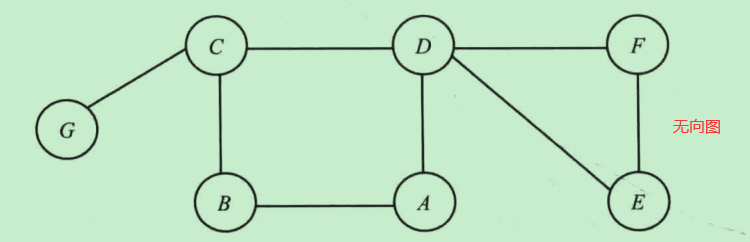
-
无环图称为树,树是不包含环的连通图
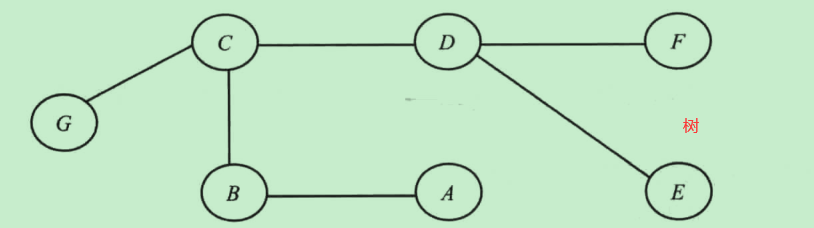
-
自环:一条连接顶点及自身的边
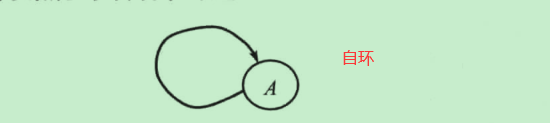
-
平行边:连接两条相同顶点对的边

-
顶点的度:关联该顶点的边的数目(有向图分为入度和出度)
-
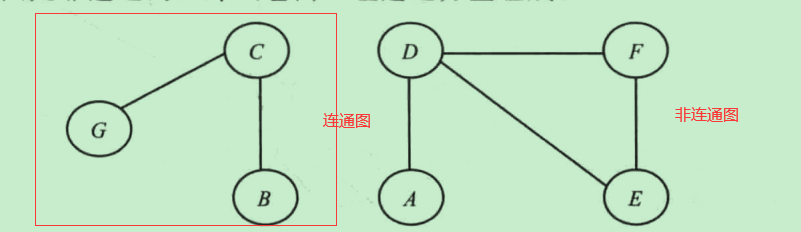
连通图:图中的每一对顶点都有路径相连
-
非连通图有一组连通分量组成
-
森林是一组不相交的树的集合
-
连通图的生成树:含有图中的n个顶点,n-1条边
-
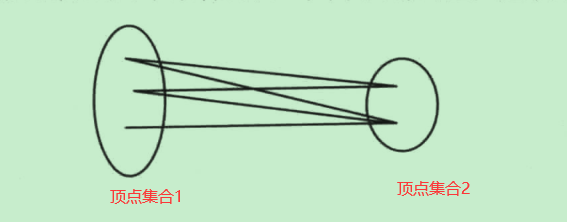
二分图:顶点被分为两个集合,所有边的两个顶点来自不同集合
-
加权图:给图中的每条边赋值一个权重
2. 图的表示方法
2.1 邻接矩阵
假设图中有V个顶点,则邻接矩阵是一个V*V大小的二维矩阵
- 对于无权图而言:如果顶点i和顶点j相邻,则设置
adj[i][j]为1或者true,不相邻则设置为0或者false - 对于加权图而言:如果顶点i和顶点j相邻,则设置
adj[i][j]为实际权值, 不相邻则设置为无穷大值
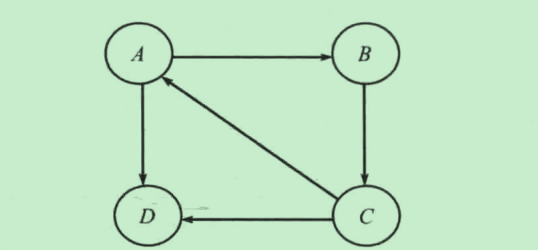

邻接矩阵适用于稠密图
2.2 邻接表
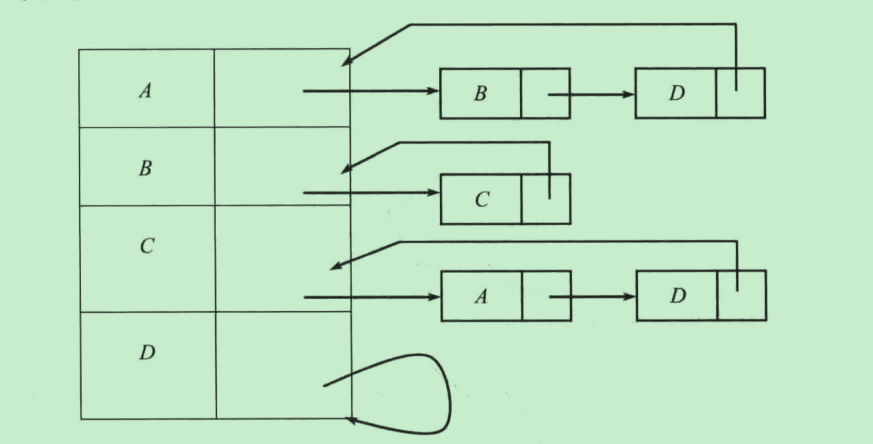
- 与某个节点v相连的节点存放在v的邻接表中
- 链表中的节点顺序会影响后续的算法执行顺序
无权图的邻接表示例:
//创建邻表表示无权值图
ArrayList<Integer> []adj=new ArrayList[8];
for(int i=0;i<8;i++)
adj[i]=new ArrayList<>();
adj[0].addAll(Arrays.asList(2,4));
adj[1].addAll(Arrays.asList(3));
adj[2].addAll(Arrays.asList(7));
adj[3].addAll(Arrays.asList(6));
........
........
adj[7].addAll(Arrays.asList(3,5));
加权图的邻接表示例1:
class Node{
int v;
double weight;
//省略构造方法
}
ArrayList<Node> []adj=new ArrayList[8];
for(int i=0;i<8;i++)
adj[i]=new ArrayList<>();
adj[0].add(new Node(1,0.25));//0-1这条边之间的权值是0.25
.......
.......
//邻接表中的节点元素是Node类型
加权图的邻接表示例2:
Edge edges[]=new Edge[16];
edges[0]=new Edge(0, 7, 0.16);
edges[1]=new Edge(2, 3, 0.17);
edges[2]=new Edge(1, 7, 0.19);
edges[3]=new Edge(0, 2, 0.26);
edges[4]=new Edge(5, 7, 0.28);
edges[5]=new Edge(1, 3, 0.29);
edges[6]=new Edge(1, 5, 0.32);
edges[7]=new Edge(2, 7, 0.34);
edges[8]=new Edge(4, 5, 0.35);
edges[9]=new Edge(1, 2, 0.36);
edges[10]=new Edge(4, 7, 0.37);
edges[11]=new Edge(0, 4, 0.38);
edges[12]=new Edge(6, 2, 0.40);
edges[13]=new Edge(3, 6, 0.52);
edges[14]=new Edge(6, 0, 0.58);
edges[15]=new Edge(6, 4, 0.93);
ArrayList<Edge> []G=new ArrayList[8];
for(int i=0;i<G.length;i++)
{
G[i]=new ArrayList<>();
}
for(Edge edge:edges)
{
int u=edge.u;
int v=edge.v;
G[u].add(edge);
//G[v].add(edge); 如果是无向图则打开这条注释
}
//1. 先创建边
//2. 将邻接表中的链表元素换成Edge类型
2.3 边的列表
使用个列表保存所有的边,缺点在于要访问某个顶点v的相邻顶点需要检查图中的所有边
示例:
class Edge{
int u;
int v;
double weight;
public Edge(int u,int v,double weight)
{
this.u=u;
this.v=v;
this.weight=weight;
}
@Override
public String toString() {
return "Edge [u=" + u + ", v=" + v + ", weight=" + weight + "]";
}
}
Edge edges[]=new Edge[16];
edges[0]=new Edge(0, 7, 0.16);
edges[1]=new Edge(2, 3, 0.17);
edges[2]=new Edge(1, 7, 0.19);
edges[3]=new Edge(0, 2, 0.26);
edges[4]=new Edge(5, 7, 0.28);
edges[5]=new Edge(1, 3, 0.29);
edges[6]=new Edge(1, 5, 0.32);
edges[7]=new Edge(2, 7, 0.34);
edges[8]=new Edge(4, 5, 0.35);
edges[9]=new Edge(1, 2, 0.36);
edges[10]=new Edge(4, 7, 0.37);
edges[11]=new Edge(0, 4, 0.38);
edges[12]=new Edge(6, 2, 0.40);
edges[13]=new Edge(3, 6, 0.52);
edges[14]=new Edge(6, 0, 0.58);
edges[15]=new Edge(6, 4, 0.93);
2.4 3种表示图的方式的比较

3. 图的遍历
3.1 深度优先遍历
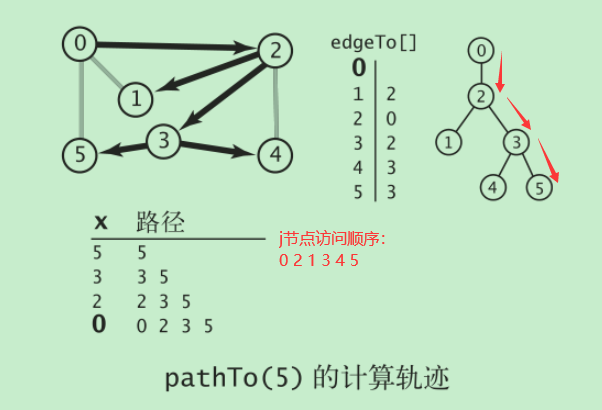
深度优先搜索(DFS)。它使用一个 boolean 数组来记录和起点连通的所有顶点。递归方法会标记给定的顶点并调用自己来访问该顶点的相邻顶点列表中所有没有被标记过的顶点。如果图是连通的,每个邻接链表中的元素都会被检查到
boolean []marked; 标记数组,标记某个节点是否被访问过
int []edgeTo; 保存遍历路径的数组,edge[u]=v标示在遍历路径中,v是u的前继节点,v—>u
int s; s表示起点
一个例子:
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
public class DFSDemo {
boolean []marked;
int []edgeTo;
int s;
public DFSDemo(ArrayList<Integer> [] adj,int s)
{
marked=new boolean[adj.length];
edgeTo=new int[adj.length];
this.s=s;
dfs(adj,s);
}
public void dfs(ArrayList<Integer> [] adj,int v)
{
marked[v]=true;
for(int w:adj[v])
{
if(!marked[w])
{
edgeTo[w]=v;
dfs(adj,w);
}
}
}
public LinkedList<Integer> pathTo(int v)
{
LinkedList<Integer> st=new LinkedList<>();
//使用栈这种数据结构 因为路径是回溯的 从目的节点反推回源节点 使用栈使得上面的元素是前面的节点
for(int x=v;x!=s;x=edgeTo[x])
st.push(x);
st.push(s);//最后添加出发节点
return st;
}
public static void main(String[] args) {
//创建邻表表示图
ArrayList<Integer> []adj=new ArrayList[6];
for(int i=0;i<6;i++)
adj[i]=new ArrayList<>();
adj[0].addAll(Arrays.asList(2,1,5));
adj[1].addAll(Arrays.asList(0,2));
adj[2].addAll(Arrays.asList(0,1,3,4));
adj[3].addAll(Arrays.asList(5,4,2));
adj[4].addAll(Arrays.asList(3,2));
adj[5].addAll(Arrays.asList(3,0));
DFSDemo dfs=new DFSDemo(adj, 0);
for(int i=0;i<=5;i++)
{
System.out.println(dfs.pathTo(i));
}
}
}
3.2 广度优先遍历
- 对于从 s 可达的任意顶点 v,广度优先搜索都能找到一条从 s 到 v 的最短路径(没有
其他从 s 到 v 的路径所含的边比这条路径更少,DFS不一定能找到最优解)
一个例子:
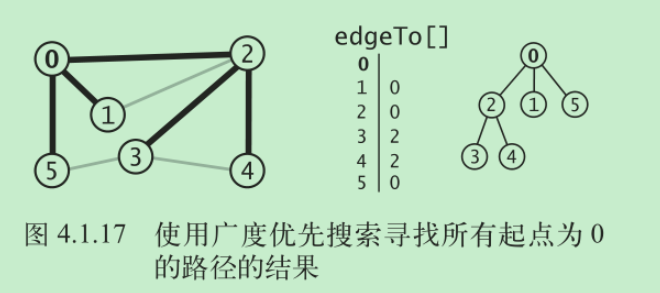
- 顶点 0 被加入队列,然后循环开始搜索
- 从队列中删去顶点0并将它的相邻顶点2、1 和 5 加入队列中,标记它们并分别将它们在 edgeTo[] 中的值设为 0
- 从队列中删去顶点 2 并检查它的相邻顶点 0 和 1,发现两者都已经被标记。将相邻的顶点 3
和 4 加入队列,标记它们并分别将它们在 edgeTo[] 中的值设为2 - 从队列中删去顶点 1 并检查它的相邻顶点 0 和 2,发现它们都已经被标记了
- 从队列中删去顶点 5 并检查它的相邻顶点 3 和 0,发现它们都已经被标记了
- 从队列中删去顶点 3 并检查它的相邻顶点 5、4 和 2,发现它们都已经被标记了
- 从队列中删去顶点 4 并检查它的相邻顶点 3 和 2,发现它们都已经被标记了
import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;
public class BFSDemo {
boolean []marked;
int []edgeTo;
int s;
public BFSDemo(ArrayList<Integer> [] adj,int s)
{
marked=new boolean[adj.length];
edgeTo=new int[adj.length];
this.s=s;
bfs(adj,s);
}
public void bfs(ArrayList<Integer> [] adj,int s)
{
Queue<Integer> q=new LinkedList<>();
q.offer(s);
marked[s]=true;
while(!q.isEmpty())
{
int v=q.poll();
for(int w:adj[v])
{
if(!marked[w])
{
edgeTo[w]=v;
marked[w]=true;
q.offer(w);
}
}
}
}
public LinkedList<Integer> pathTo(int v)
{
LinkedList<Integer> st=new LinkedList<>();
//使用栈这种数据结构 因为路径是回溯的 从目的节点反推回源节点 使用栈使得上面的元素是前面的节点
for(int x=v;x!=s;x=edgeTo[x])
st.push(x);
st.push(s);//最后添加出发节点
return st;
}
public static void main(String[] args) {
ArrayList<Integer> []adj=new ArrayList[6];
for(int i=0;i<6;i++)
adj[i]=new ArrayList<>();
adj[0].addAll(Arrays.asList(2,1,5));
adj[1].addAll(Arrays.asList(0,2));
adj[2].addAll(Arrays.asList(0,1,3,4));
adj[3].addAll(Arrays.asList(5,4,2));
adj[4].addAll(Arrays.asList(3,2));
adj[5].addAll(Arrays.asList(3,0));
BFSDemo dfs=new BFSDemo(adj, 0);
for(int i=0;i<=5;i++)
{
System.out.println(dfs.pathTo(i));
}
}
}
3.3 DFS与BFS的比较
- DFS的内存消耗远远小于BFS,DFS不需要存储每一层孩子节点的指针
- DFS类似于树的前序遍历,BFS类似于树的层次遍历
- DFS查找的速度较快
- 如果查找的答案所在的高度较低(靠近树的顶端)—BFS
- 如果查找的答案所在的高度较深(靠近树的底端)—DFS
4. 拓扑排序
拓扑排序是对有向无环图中顶点的排序,对于任意一条边,箭头开始处的节点排在箭头结束处的节点前面,一个有向无环图中的拓扑序列可能不唯一
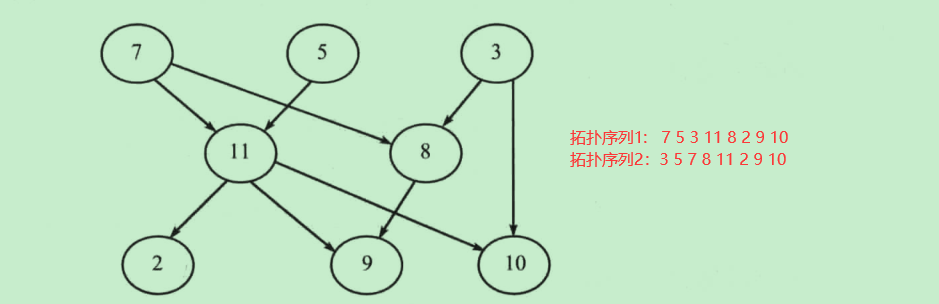
如何得到一个拓扑序列?
- 计算所有顶点的入度
- 讲入度为0的节点加入队列
- 将队列中入度为0的节点v出队,并将与节点v相邻的节点的入度减去1,如果有哪个节点减去1之后入度为0,则将该节点也加入队列
- 重复第3步,知道队列为空
按以上步骤操作后的出队序列就是一个拓扑排序序列
5. 最短路径算法Dijkstra
- 是一种贪心算法:总是选取最接近源点的顶点
- 采用优先级队列并按照到s(源点)的距离来存储未被访问过的顶点
- 不能处理权值为负的情况
思想:
-
设置两个顶点集S和T,集合S中存放已经找到最短路径的顶点,集合T中存放着当前还未找到最短路径的顶点
-
初始状态下,集合S中只包含源点V1,T中为除了源点之外的其余顶点,此时源点到各顶点的最短路径为两个顶点所连的边上的权值,如果源点V1到该顶点没有边,则最小路径为无穷大
-
从集合T中选取到源点V1的路径长度最短的顶点Vi加入到集合S中
-
修改源点V1到集合T中剩余顶点Vj的最短路径长度。新的最短路径长度值为Vj原来的最短路径长度值与顶点Vi的最短路径长度加上Vi到Vj的路径长度值中的较小者;
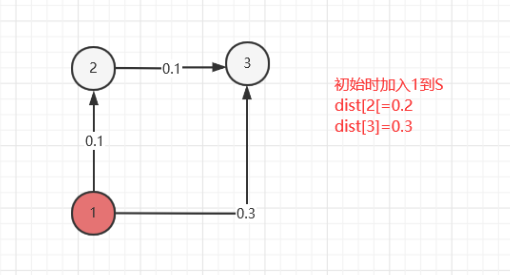
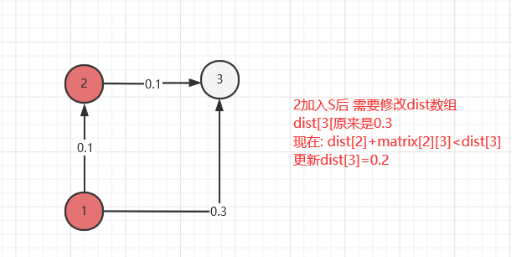
-
不断重复步骤3、4,直至集合T的顶点全部加入到集合S中
实例:
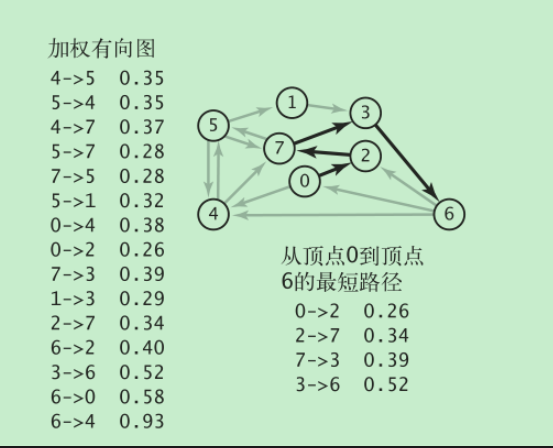
不使用优先级队列:
import java.util.ArrayList;
import java.util.LinkedList;
public class DijstraDemo {
int N;//N个节点
int []vertexs;//保存顶点
int []pre;//保存前驱节点
double [][]matrix;//邻接矩阵
double []dist;//保存到某个顶点的距离
boolean []visited;//标记顶点是否被访问
public DijstraDemo(int N)
{
this.N=N;
vertexs=new int[N];
pre=new int[N];
dist=new double[N];
matrix=new double[N][N];
visited=new boolean[N];
}
public void setVertexs(int []vertexs)
{
this.vertexs=vertexs;
}
public void setMatrix(double [][]matrix)
{
this.matrix=matrix;
}
public void digstra(int start)
{
for(int v=0;v<N;v++)
{
visited[v]=false;
dist[v]=matrix[start][v];
// if(dist[v]<Double.POSITIVE_INFINITY)
// pre[v]=start;
// else
pre[v]=start;
}
dist[start]=0;
visited[start]=true;
for(int i=0;i<N;i++)
{
double min=Double.POSITIVE_INFINITY;
int index=-1;
//此轮for循环找到与start节点最近的节点
//从集合T中选取到源点V1的路径长度最短的顶点Vi加入到集合S中
for(int j=0;j<N;j++)
{
if(!visited[j])
{
if(dist[j]<min)
{
index=j;
min=dist[j];
}
}
}
if(index!=-1)
visited[index]=true;
else //index==-1说明此轮没有找到index 后面的更新操作可以跳过
continue;
//此轮for循环更新start到k的距离
for(int k=0;k<N;k++)
{
if(!visited[k])
{
if(matrix[index][k]!=Double.POSITIVE_INFINITY&&matrix[index][k]+min<dist[k])
{
dist[k]=matrix[index][k]+min;
pre[k]=index;//更新前驱节点
}
}
}
}
}
//打印路径
public LinkedList<Integer> path(int start,int end)
{
LinkedList<Integer> st=new LinkedList<>();
for(int x=end;x!=start;x=pre[x])
st.push(x);
st.push(start);
return st;
}
public static void main(String[] args) {
int []vertexs={0,1,2,3,4,5,6,7};
double max=Double.POSITIVE_INFINITY;
double [][]matrix={
{max,max,0.26,max,0.38,max,max,max},
{max,max,max,0.29,max,max,max,max},
{max,max,max,max,max,max,max,0.34},
{max,max,max,max,max,max,0.52,max},
{max,max,max,max,max,0.35,max,0.37},
{max,0.32,max,max,0.35,max,max,0.28},
{0.58,max,0.40,max,0.93,max,max,max},
{max,max,max,0.39,max,0.28,max,max}
};
DijstraDemo demo=new DijstraDemo(8);
demo.setVertexs(vertexs);
demo.setMatrix(matrix);
demo.digstra(0);
for(int i=0;i<8;i++)
{
System.out.print("0->"+i);
System.out.print(" path:"+demo.path(0, i));
System.out.println(" distance:"+demo.dist[i]);
}
}
}
邻接表+优先级队列:
package dijkstra;
import java.util.ArrayList;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.PriorityQueue;
public class DijkstrDemo {
public double MAX=Double.POSITIVE_INFINITY;
int []pre;//保存前驱节点
boolean []visited;//标记顶点是否被访问
public double []disTo;
public int n;
public void dijkstra(ArrayList<Edge> G[],int n,int start) {
this.n=n;
pre=new int[n];
visited=new boolean[n];
disTo=new double[n];
for(int v=0;v<n;v++)
{
visited[v]=false;
disTo[v]=MAX;//设置初始距离都为MAX
pre[v]=start;
}
//小顶堆 堆顶元素的距离最短
PriorityQueue<Vertex> pq=new PriorityQueue<Vertex>(new Comparator<Vertex>() {
public int compare(Vertex o1, Vertex o2) {
if(o1.dis<o2.dis)
return -1;
else {
return 1;
}
}
});
pq.offer(new Vertex(start, 0));
disTo[start]=0;
while(!pq.isEmpty())
{
Vertex v=pq.poll();//从队列中取出当前可以到达的最短距离的点
int num=v.num;
double dis=v.dis;
if(visited[num])//num节点已经被访问
continue;
visited[num]=true;
for(Edge edge:G[num])
{
if(num!=edge.from)//只找以节点num为起点的边
continue;
int to=edge.to;
//start->to节点的距离可以更新 num点作为中间点来更新start到to的距离
if(!visited[to]&&disTo[to]>v.dis+edge.weight)
{
disTo[to]=dis+edge.weight;//更新距离
pre[to]=num;
pq.add(new Vertex(to, disTo[to]));//将新的节点加入队列
}
}
}
}
public LinkedList<Integer> path(int start,int end)
{
LinkedList<Integer> st=new LinkedList<>();
for(int x=end;x!=start;x=pre[x])
st.push(x);
st.push(start);
return st;
}
public static void main(String[] args) {
Edge edges[]=new Edge[15];
edges[0]=new Edge(4, 5, 0.35);
edges[1]=new Edge(5, 4, 0.35);
edges[2]=new Edge(4, 7, 0.37);
edges[3]=new Edge(5, 7, 0.28);
edges[4]=new Edge(7, 5, 0.28);
edges[5]=new Edge(5, 1, 0.32);
edges[6]=new Edge(0, 2, 0.26);
edges[7]=new Edge(7, 3, 0.39);
edges[8]=new Edge(1, 3, 0.29);
edges[9]=new Edge(2, 7, 0.34);
edges[10]=new Edge(6, 2, 0.40);
edges[11]=new Edge(3, 6, 0.52);
edges[12]=new Edge(6, 0, 0.58);
edges[13]=new Edge(6, 4, 0.93);
edges[14]=new Edge(0, 4, 0.38);
ArrayList<Edge> []G=new ArrayList[8];
for(int i=0;i<8;i++)
G[i]=new ArrayList<Edge>();
for(Edge edge:edges)
{
int from=edge.from;
int to=edge.to;
G[from].add(edge);
}
DijkstrDemo demo=new DijkstrDemo();
demo.dijkstra(G, 8, 0);
for(int i=0;i<8;i++)
{
System.out.print("0->"+i);
System.out.print(" path:"+demo.path(0, i));
System.out.println(" distance:"+demo.disTo[i]);
}
}
}
class Vertex {
int num;
double dis;
public Vertex(int num, double dis) {
this.num = num;
this.dis = dis;
}
@Override
public String toString() {
return "Vertex [num=" + num + ", dis=" + dis + "]";
}
}
public class Edge {
int from;
int to;
double weight;
public Edge(int from, int to, double weight) {
this.from = from;
this.to = to;
this.weight = weight;
}
@Override
public String toString() {
return "Edge [from=" + from + ", to=" + to + ", weight=" + weight + "]";
}
}
不使用堆的时间复杂度:O(E+V*V)
使用堆的时间复杂度:O(ElogV)
6. 最小生成树算法
图的生成树:包含图中n个顶点和n-1条边,图的生成树不唯一,比如下面的图就有4个生成树:

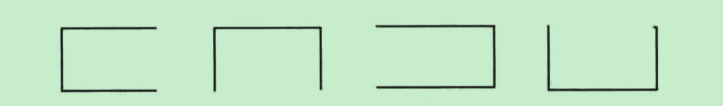
最小生成树:对于有向图而言,最后得到的生成树的各条边的权值之和最小
6.1 Prim算法
思想:先加入一个顶点,然后从与该顶点相邻且未被加入的顶点形成的边中选择权值最小的,然后再从加入的边的顶点形成的边中再选择权值最小的…反复这个过程,知道有v个顶点和v-1条边
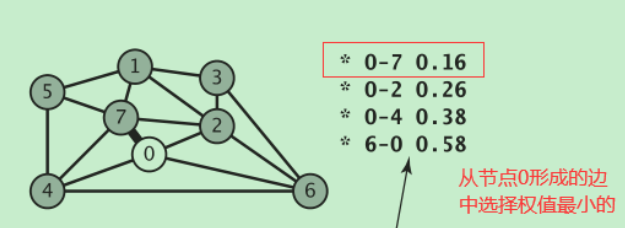
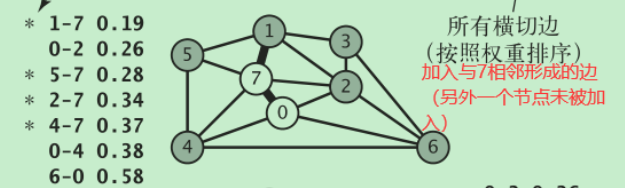
Prim算法操作和Dijkstra算法类似
代码实现:
import java.util.ArrayList;
import java.util.Comparator;
import java.util.LinkedList;
import java.util.PriorityQueue;
class Edge2 {
int u;
int v;
double weight;
public Edge2(int u, int v, double weight) {
this.u = u;
this.v = v;
this.weight = weight;
}
public int other(int w)//返回与w形成的边的另外一个顶点
{
if(w==u)
return v;
else
return u;
}
@Override
public String toString() {
return "Edge2 [u=" + u + ", v=" + v + ", weight=" + weight + "]";
}
}
public class PrimDemo {
static boolean []marked;
static LinkedList<Edge2> mst;
static PriorityQueue<Edge2> pq;
public static void prim(ArrayList<Edge2> []G)
{
marked=new boolean[G.length];
mst=new LinkedList<>();
//队列中的边按权值由小到大排列
pq=new PriorityQueue<>(new Comparator<Edge2>() {
@Override
public int compare(Edge2 o1, Edge2 o2) {
if(o1.weight<=o2.weight)
return -1;
else
return 1;
}
});
visit(G, 0);//先访问顶点0
while(!pq.isEmpty())
{
Edge2 Edge2=pq.poll();
int v=Edge2.v,u=Edge2.u;//拿到当前队列中权值最小的边
if(marked[v]&&marked[u])//该边的两个顶点都已经被选则 跳过
continue;
mst.offer(Edge2);//否则加入该边
if(!marked[v])//v未被访问 访问v
visit(G, v);
if(!marked[u])//u未被访问 访问u
visit(G, u);
}
}
public static void visit(ArrayList<Edge2> []G,int v)
{
marked[v]=true;//v标记为已经访问
for(Edge2 edge:G[v])
{
if(!marked[edge.other(v)])//v所在的边的另外一个节点没有被加入
pq.offer(edge);//该边符合候选条件
}
}
public static void main(String[] args) {
Edge2 Edge2s[]=new Edge2[16];
Edge2s[0]=new Edge2(0, 7, 0.16);
Edge2s[1]=new Edge2(2, 3, 0.17);
Edge2s[2]=new Edge2(1, 7, 0.19);
Edge2s[3]=new Edge2(0, 2, 0.26);
Edge2s[4]=new Edge2(5, 7, 0.28);
Edge2s[5]=new Edge2(1, 3, 0.29);
Edge2s[6]=new Edge2(1, 5, 0.32);
Edge2s[7]=new Edge2(2, 7, 0.34);
Edge2s[8]=new Edge2(4, 5, 0.35);
Edge2s[9]=new Edge2(1, 2, 0.36);
Edge2s[10]=new Edge2(4, 7, 0.37);
Edge2s[11]=new Edge2(0, 4, 0.38);
Edge2s[12]=new Edge2(6, 2, 0.40);
Edge2s[13]=new Edge2(3, 6, 0.52);
Edge2s[14]=new Edge2(6, 0, 0.58);
Edge2s[15]=new Edge2(6, 4, 0.93);
//需要知道和顶点v相邻的边有哪些
ArrayList<Edge2> []G=new ArrayList[8];
for(int i=0;i<G.length;i++)
{
G[i]=new ArrayList<>();
}
for(Edge2 Edge2:Edge2s)
{
int u=Edge2.u;
int v=Edge2.v;
G[u].add(Edge2);
G[v].add(Edge2);
}
prim(G);
System.out.println(mst);
}
}
时间复杂度:O(ElogV)
6.2 Kruskal算法
思想:
现在有一个图(可能有环),将图中的边按权重顺序(从小到大)进行处理,将边加入最小生成树中,加入的边不会与已经加入的边形成环,直到树中有V-1条边为止(V是结点数,最后的最小生成树中有V个节点,V-1条边)
Kruskal 算法的计算一幅含有 V 个顶点和 E 条边的连通加权无向图的最小生成
树所需的空间和 E 成正比,所需的时间和 ElogE 成正比(最坏情况)
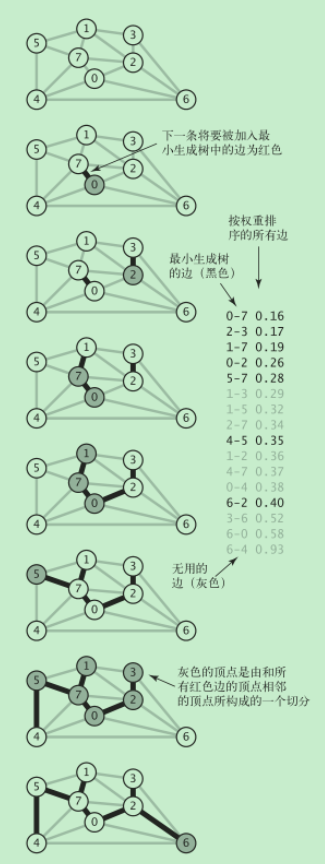
代码实现:
采用一个优先级队列保存边,使得堆顶的边的权值最小,使用并查集判断加入的两条边是否连通
import java.util.ArrayList;
import java.util.Comparator;
import java.util.PriorityQueue;
class Edge{
int u;
int v;
double weight;
public Edge(int u,int v,double weight)
{
this.u=u;
this.v=v;
this.weight=weight;
}
@Override
public String toString() {
return "Edge [u=" + u + ", v=" + v + ", weight=" + weight + "]";
}
}
class UF{
int count;
int parent[];
int sz[];
public UF(int N)
{
parent=new int[N];
sz=new int[N];
count=N;
for(int i=0;i<N;i++)
{
parent[i]=i;
sz[i]=1;
}
}
public int find(int p)
{
while(p!=parent[p])
{
parent[p]=parent[parent[p]];
p=parent[p];
}
return p;
}
public boolean connected(int p,int q)
{
return find(p)==find(q);
}
public void union(int p,int q)
{
int pRoot=find(p);
int qRoot=find(q);
if(pRoot==qRoot)
return;
if(sz[pRoot]<sz[qRoot])
{
parent[pRoot]=qRoot;
sz[qRoot]+=sz[pRoot];
}
else
{
parent[qRoot]=pRoot;
sz[pRoot]+=sz[qRoot];
}
count--;
}
}
public class KruskalDemo {
public static void main(String[] args) {
ArrayList<Edge> list=new ArrayList<>();
PriorityQueue<Edge> pq=new PriorityQueue<>(new Comparator<Edge>() {
@Override
public int compare(Edge o1, Edge o2) {
if(o1.weight<=o2.weight)
return -1;
else
return 1;
}
});
Edge edges[]=new Edge[16];
edges[0]=new Edge(0, 7, 0.16);
edges[1]=new Edge(2, 3, 0.17);
edges[2]=new Edge(1, 7, 0.19);
edges[3]=new Edge(0, 2, 0.26);
edges[4]=new Edge(5, 7, 0.28);
edges[5]=new Edge(1, 3, 0.29);
edges[6]=new Edge(1, 5, 0.32);
edges[7]=new Edge(2, 7, 0.34);
edges[8]=new Edge(4, 5, 0.35);
edges[9]=new Edge(1, 2, 0.36);
edges[10]=new Edge(4, 7, 0.37);
edges[11]=new Edge(0, 4, 0.38);
edges[12]=new Edge(6, 2, 0.40);
edges[13]=new Edge(3, 6, 0.52);
edges[14]=new Edge(6, 0, 0.58);
edges[15]=new Edge(6, 4, 0.93);
for(Edge edge:edges)
{
pq.offer(edge);
}
//一共8个顶点
UF uf=new UF(8);
double minCost=0;
while(!pq.isEmpty())
{
Edge edge=pq.poll(); //堆顶的边是权值最小的
int u=edge.u;
int v=edge.v;
double w=edge.weight;
if(uf.connected(u, v))// u v已经连通了 再加入u-v这条边会形成环
continue;
if(uf.count==1) //只有一个连通分量说明最小生成树已经包含n个节点
break;
list.add(edge); //记录加入的边
uf.union(u, v);
minCost+=w;
}
System.out.println("minCost:"+minCost);
System.out.println(list);
}
}
Prim算法优先选择顶点,kruskal优先选择边























 753
753











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










