【铅垂线法的加速】 \huge\textsf{【铅垂线法的加速】} 【铅垂线法的加速】
想必大家都做过这样的题目: \textsf{想必大家都做过这样的题目:} 想必大家都做过这样的题目:
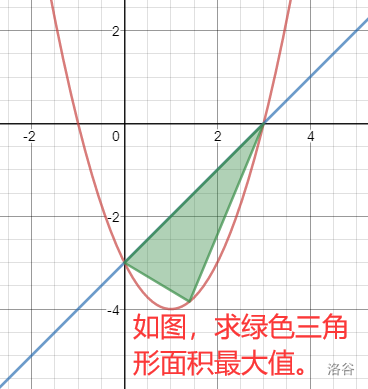
方法是铅锤线法。 \textsf{方法是铅锤线法。} 方法是铅锤线法。
先求蓝色直线解析式,然后与抛物线解析式相减,求出高度差最大值,最后计算出面积最大值。 \textsf{先求蓝色直线解析式,然后与抛物线解析式相减,求出高度差最大值,最后计算出面积最大值。} 先求蓝色直线解析式,然后与抛物线解析式相减,求出高度差最大值,最后计算出面积最大值。
但是如果善用数学归纳法,就能发现: \textsf{但是如果善用数学归纳法,就能发现:} 但是如果善用数学归纳法,就能发现:
三角形第三个顶点的横坐标与抛物线与直线两交点的中点的横坐标相等时,面积最大。 \color{#12c2e9}\large\texttt{三角形第三个顶点的横坐标与抛物线与直线两交点的中点的横坐标相等时,面积最大。} 三角形第三个顶点的横坐标与抛物线与直线两交点的中点的横坐标相等时,面积最大。
证: \textsf{证:} 证:
设抛物线: y = a ( x − m ) ( x − n ) = a x 2 − a ( m + n ) x + a m n \textsf{设抛物线:}y=a(x-m)(x-n)=ax^{2}-a(m+n)x+amn 设抛物线:y=a(x−m)(x−n)=ax








 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 766
766

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








