【物理】不脱离外圆面问题

$$\left|\begin{array}{c}\text{ 不脱离外圆面问题 }\\ \text{ Nightguard Series. }\end{array}\right|$$

---

整理自 https://www.bilibili.com/video/BV1iK4y1Q7mc?p=8（黄夫人）

问题一

如图，小物块受到轻微扰动，从一固定的光滑半圆面上最高点 $A$ 处由静止滑下，试分析小物块的运动过程。

小物块会沿圆面圆周运动吗？

---

先思考小物块会不会做圆周运动。

做圆周运动需要向心力，下滑过程中小物块 $v$ 增大，重力指向圆心的分力不断接近0 ，则必有一点处重力的分力不足以提供向心力，小物块脱离半圆面。接下来具体分析过程。

设滑离处为 $P$：

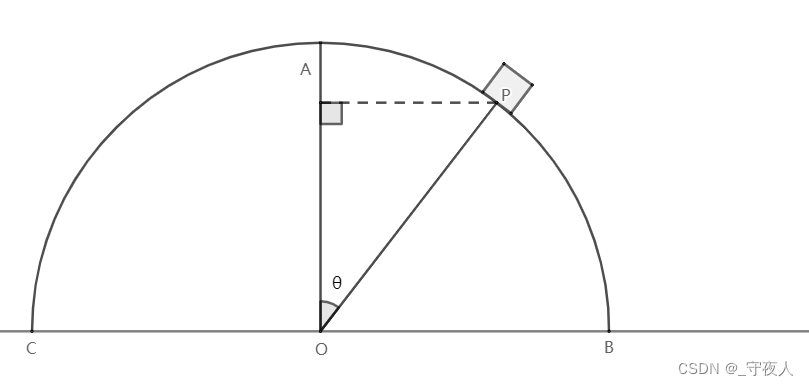
设 $\angle POA=\theta$

小物块在 $P$ 处脱离半圆面，则运动到 $P$ 点瞬间，半圆面对它的作用力 $F_N=0$

所以重力的分力提供向心力，

$$mg\cos \theta =m\frac{v_P^2}{r}$$

小物块运动到 $P$ 处时，由能量守恒得

$$mgr(1-\cos \theta )=\frac{1}{2}m{v}_P^2$$

联立化简得 $\cos \theta =\frac{2}{3}.$

因此小物块会在距离平面 $\frac{2}{3}r$ 的高度脱离半圆面。

---

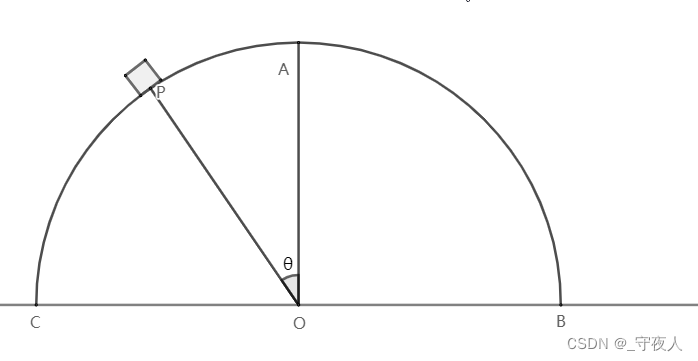
问题一

如图，小物块以一初速度从 $P$ 点开始 沿 一固定的光滑 半圆面运动 到其最高点 $A$ 处，求小物块到达 $A$ 点时最大速度。

这不是能量守恒吗？

---

请注意：小物块需要沿半圆面运动，如果初速度过大则可能会出现脱离的情况

$$\text{试分析小物块在地月轨道转移中的运动过程.jpg}$$

接下来正经分析。

同上一题，小物块在 $P$ 点速度最大时 $F_N=0$，重力的分力提供向心力，

$$mg\cos \theta =m\frac{v_P^2}{r}$$

到达 $A$ 点时能量守恒得

$$mgr(1-\cos \theta )=\frac{1}{2}m{v}_P^2-\frac{1}{2}m{v}_A^2$$

代入数据计算即可。