封闭性(closure)
封闭性,即闭包 (数学)。数学中,若对某个集合的成员进行一种运算,生成的仍然是这个集合的成员,则该集合被称为在这个运算下闭合。
例子:
5*5的矩阵关于加法和乘法关系是闭包的,因为两个 5 + 5 矩阵的总和是另一个 5 *5 矩阵。(乘法同理)
奇数的加法,乘法关系就不具备闭包关系。
二元运算(Binary operation)
二元运算(Binary operation)作用于两个对象的运算。
作用于一个对象的运算称为一元运算(unary operation)
例子:
集交集(set intersection)是二进制操作,因为它组合了两个集来生成新集
取逆(transpose)是一个一元运算。
交换性(Commutative)
如果,对象的顺序不影响二进制操作的结果,则说该操作是交换的。

例子:
普通矩阵乘法不是交换运算

布尔矩阵的联接和相遇是交换操作

结合性(Associative)
定义:
分配(distributive property)
定义:
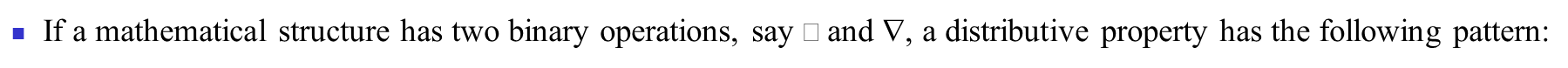
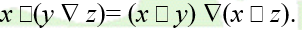
德.摩根律(De Morgan‘s laws)
定义:

运算中的单位元(Identity)
单位元(英文常写作Identity Element,即IE)是集合里的一种特别的元,与该集合里的运算(可理解为实数里的*,但并不局限于)有关。当它和其他元素结合时,并不会改变那些元素。也叫幺元(么元)。

一个运算中的单位元是唯一的
设 (S,)为一带有一二元运算 的集合S(称之为原群),则S内的一元素e被称为左单位元若对所有在S内的a而言,e*a=a;
举例:
对应于加法的单位元称之为加法单位元(通常被标为0),而对应于乘法的单位元则称之为乘法单位元(通常被标为1)。这一区分大多被用在有两个二元运算的集合上,比如环。
证明一个运算中的单位元是唯一的:
假设存在另一个单位元 i
则有:
又因为e也是单位元
则有:

因此e=i;
矩阵中的单位元
对于一个n阶矩阵,对角矩阵(In)是其关于乘法的单位元,而零矩阵(zero matrix)是其关于加法的单位元。
逆元(Inverse)
如果在一个二元运算中两个对象的运算结果是该运算的单位元,那么就认为这两个对象互为逆元。

如果运算关系满足结合律,那么x有的逆元是唯一的。

证明:
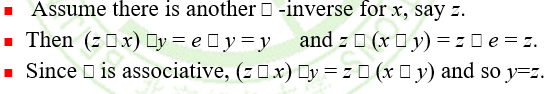
举例:
对于一个n阶矩阵每一个矩阵A=[aij]对于矩阵的加法和减法都有逆元-A=[-aij];
对于一个n阶矩阵只有矩阵全单位矩阵E对于矩阵的乘法和除法有-E;
二元运算的满足条件
- 二元运算在集合A中必须处处定义,满足

- 必须满足:
1.函数在集合A中的运算结果还包含在A中
2.每个有序的对仅分配一个 A 元素(只有一个运算结果,且该结果在A集合中)
(即定义在集合A中的关系必须是封闭的)
举例:
1.定义在整数集合内的加法运算是二元运算
(运算结果都是整数)
2.定义在实数集合的除法运算不是二元运算
(3/0在实数集合中没有定义)
3.定义在正整数集合内的减法运算不是二元运算
(2-5的结果不属于正整数集合)
运算表
如果A是一个有限集合,我们可以用一个运算表定义一个二元运算。

如果集合A={a,b},在集合A中可以定义多少中二元运算?
一共有24个运算关系
二元运算的性质
- 可交换的(Commutative)
真值表关于对角线对称 - 可结合的(Associative)
- 幂等的(Idempotent)
aa=a;
解释:设S为一具有作用于其自身的二元运算的集合,则S的元素s称为幂等的(相对于)当
s s = s.
特别的是,任一单位元都是幂等的。若S的所有元素都是幂等的话,则其二元运算被称做是幂等的。例如,联集和交集的运算便都是幂等的(aUa=a…)(注意s是一个集合,有点像传递关系的Rn=R)
























 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








