本文记录周志华《机器学习》贝叶斯分类内容:***(文中公式内容均来自周志华《机器学习》)***
贝叶斯决策论:是概率框架下实施决策的基本方法,对于分类任务来说,在所有相关概率都已知的理想情形下,贝叶斯决策论考虑如何基于这些概率和误判来选择最优的类别标记。
机器学习所实现的根据训练样本估计后验概率
P
(
c
∣
x
)
P(c|x)
P(c∣x)主要有两种方法:1.先对联合概率分布
P
(
x
,
c
)
P(x,c)
P(x,c)建模,然后再由此获得
P
(
c
∣
x
)
P(c|x)
P(c∣x)(判别式模型,决策树、BP神经网络、支持向量机均属如此);2.基于训练数据D来估计先验P©和似然P(x|c),再计算
P
(
c
∣
x
)
P(c|x)
P(c∣x)。
分类任务:
- 假设由N中可能的类别,即 γ = { c 1 , c 2 , . . . c N } {\gamma = \{ {c_1},{c_2},...{c_N}\} } γ={c1,c2,...cN}, λ i j {\lambda _{ij}} λij是将一个真实标记为 c j {c_j} cj的样本误分类为 c i {c_i} ci所产生的损失。故在样本x上的条件风险,即将样本x分类为 c i {c_i} ci所产生的期望损失,为: R ( c i ∣ x ) = ∑ j = 1 N λ i j P ( c j ∣ x ) R({c_i}|x) = \sum\limits_{j = 1}^N {{\lambda _{ij}}} P({c_j}|x) R(ci∣x)=j=1∑NλijP(cj∣x)
- 为降低总体风险,只需在每个样本上选择那个使条件风险 R ( c ∣ x ) R(c|x) R(c∣x)最小的类别标记,为 h ∗ ( x ) = arg min c ∈ γ R ( c ∣ x ) {{h^*}(x) = \mathop {\arg \min }\limits_{c \in \gamma } R(c|x)} h∗(x)=c∈γargminR(c∣x),式子中 h ∗ {h^*} h∗为贝叶斯最优分类器。
- 对于分类任务来说,误判损失为
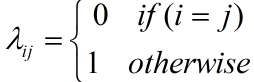
- 此时条件风险: R ( c ∣ x ) = 1 − P ( c ∣ x ) R(c|x) = 1 - P(c|x) R(c∣x)=1−P(c∣x);最优分类器可写为: h ∗ ( x ) = arg min c ∈ γ P ( c ∣ x ) {h^*}(x) = \mathop {\arg \min }\limits_{c \in \gamma } P(c|x) h∗(x)=c∈γargminP(c∣x)
- 基于贝叶斯定理, P ( c ∣ x ) = P ( c ) P ( x ∣ c ) P ( x ) P(c|x) = {{P(c)P(x|c)} \over {P(x)}} P(c∣x)=P(x)P(c)P(x∣c),式中P©是类“先验”概率,P(x|c)是样本x相对于类标记c的类条件概率(或成为“似然”)。
朴素贝叶斯分类器:
朴素贝叶斯分类器采用“属性条件独立性假设”:对已知类别,假设所有属性相互独立。
因此上式可写为
P
(
c
∣
x
)
=
P
(
c
)
P
(
x
)
∏
i
=
1
d
P
(
x
i
∣
c
)
{P(c|x) = {{P(c)} \over {P(x)}}\prod\limits_{i = 1}^d {P({x_i}|c)} }
P(c∣x)=P(x)P(c)i=1∏dP(xi∣c),
x
i
{{x_i}}
xi为x在第i个属性上的取值,d为属性数目。
式中:
P
(
c
)
=
∣
D
c
∣
∣
D
∣
P(c) = {{|{D_c}|} \over {|D|}}
P(c)=∣D∣∣Dc∣,对于离散属性
P
(
x
i
∣
c
)
=
∣
D
c
,
x
i
∣
∣
D
c
∣
P({x_i}|c) = {{|{D_{c,{x_i}}}|} \over {|{D_c}|}}
P(xi∣c)=∣Dc∣∣Dc,xi∣;对于连续属性可考虑概率密度函数,假定
P
(
x
i
∣
c
)
P({x_i}|c)
P(xi∣c)符合
N
(
μ
c
,
i
,
σ
c
,
i
2
)
N({\mu _{c,i}},\sigma _{c,i}^2)
N(μc,i,σc,i2)模型,则有
P
(
x
i
∣
c
)
=
1
2
π
σ
c
,
i
exp
(
−
(
x
i
−
μ
c
,
i
)
2
2
σ
c
,
i
2
)
P({x_i}|c) = {1 \over {\sqrt {2\pi } {\sigma _{c,i}}}}\exp ( - {{{{({x_i} - {\mu _{c,i}})}^2}} \over {2\sigma _{c,i}^2}})
P(xi∣c)=2πσc,i1exp(−2σc,i2(xi−μc,i)2)。
对于连续属性中,存在的未知量,可采用极大似然估计:根据数据采样来估计概率分布参数。
令
D
c
{{\rm{D}}_{\rm{c}}}
Dc表示训练集中第c类样本组成的集合,假设这些样本是独立同分布的,
P
(
x
∣
θ
c
)
是
概
率
密
度
函
数
。
{P({\rm{x}}|{\theta _{\rm{c}}})}是概率密度函数。
P(x∣θc)是概率密度函数。则参数
θ
c
{\theta _{\rm{c}}}
θc对于数据集的似然是
P
(
D
c
∣
θ
c
)
=
∏
x
∈
D
c
P
(
x
∣
θ
c
)
{P({{\rm{D}}_{\rm{c}}}|{\theta _{\rm{c}}}) = \prod\limits_{x \in {{\rm{D}}_{\rm{c}}}} {P({\rm{x}}|{\theta _{\rm{c}}})}}
P(Dc∣θc)=x∈Dc∏P(x∣θc),为防止连乘操作易造成下溢,通常使用对数似然:
L
L
(
θ
c
)
=
log
P
(
D
c
∣
θ
c
)
=
∑
x
∈
D
c
log
P
(
x
∣
θ
c
)
LL({\theta _{\rm{c}}}) = \log P({{\rm{D}}_{\rm{c}}}|{\theta _{\rm{c}}}) = \sum\limits_{x \in {{\rm{D}}_{\rm{c}}}} {\log } P({\rm{x}}|{\theta _{\rm{c}}})
LL(θc)=logP(Dc∣θc)=x∈Dc∑logP(x∣θc),然后求导后的零值点即可。放到正态分布中为:
μ
c
=
1
∣
D
c
∣
∑
x
∈
D
c
x
{\mu _c} = {1 \over {|{D_c}|}}\sum\limits_{x \in {{\rm{D}}_{\rm{c}}}} x
μc=∣Dc∣1x∈Dc∑x
σ
2
=
1
∣
D
c
∣
∑
x
∈
D
c
(
x
−
μ
c
)
(
x
−
μ
c
)
T
{\sigma ^2} = {1 \over {|{D_c}|}}\sum\limits_{x \in {{\rm{D}}_{\rm{c}}}} {(x - {\mu _c}){{(x - {\mu _c})}^T}}
σ2=∣Dc∣1x∈Dc∑(x−μc)(x−μc)T
对于某个属性值没有出现过的情况下,在计算时会出现连乘为零的情况。因此应在估计概率值时通常要进行“平滑”,常用“拉普拉斯修正”:令N表示训练集D中可能的类别数, N i {N_i} Ni表示第i个属性可能的取值数,则上式可修正为: P ( c ) = ∣ D c ∣ + 1 ∣ D ∣ + N P(c) = {{|{{\rm{D}}_{\rm{c}}}| + 1} \over {|D| + N}} P(c)=∣D∣+N∣Dc∣+1, P ( x i ∣ c ) = ∣ D c , x i ∣ + 1 ∣ D c ∣ + N i P({x_i}|c) = {{|{{\rm{D}}_{{\rm{c,}}{{\rm{x}}_i}}}| + 1} \over {|{{\rm{D}}_{\rm{c}}}| + {N_i}}} P(xi∣c)=∣Dc∣+Ni∣Dc,xi∣+1。
EM算法:对于存在隐变量式,令X表示已观测变量集,Z为隐变量集,
θ
{\theta}
θ为模型参数,如果对
θ
{\theta}
θ做极大似然估计,
L
L
(
θ
∣
X
,
Z
)
=
ln
P
(
X
,
Z
∣
θ
)
LL(\theta |X,Z) = \ln P(X,Z|\theta )
LL(θ∣X,Z)=lnP(X,Z∣θ),由于Z为隐变量,上式无法直接求解,此时我们可通过对Z计算期望,来最大化已观测数据。
EM算法:是一种跌打算法,若参数
θ
{\theta}
θ已知,则可根据训练数据推断出最优隐变量Z的值(E步);反之,若Z的值已知,则可对参数
θ
{\theta}
θ做极大似然估计。
于是,以初始值
θ
0
{\theta ^0}
θ0为七点,迭代执行:1.基于
θ
t
{\theta ^{\rm{t}}}
θt推断Z的期望,记为
Z
t
{Z^t}
Zt;2.基于已观测变量X和
Z
t
{Z^t}
Zt对参数
θ
{\theta}
θ做极大似然估计,记为
θ
t
+
1
{\theta ^{{\rm{t + 1}}}}
θt+1。
示例:复旦-机器学习课程 第十讲 EM 算法(这个视频讲的很好)
若存在K个高斯分布
N
(
μ
1
,
σ
1
2
)
N({\mu _1},\sigma _1^2)
N(μ1,σ12)、
N
(
μ
2
,
σ
2
2
)
N({\mu _2},\sigma _2^2)
N(μ2,σ22)…
N
(
μ
k
,
σ
k
2
)
N({\mu _k},\sigma _k^2)
N(μk,σk2),在其中随机抽取,故有w1,w2…wk概率值,且
∑
i
=
1
k
w
i
=
1
\sum\limits_{i = 1}^k {{w_i}} = 1
i=1∑kwi=1。则X的密度函数为
w
1
f
1
(
x
)
+
.
.
.
+
w
k
f
k
(
x
)
{w_1}{f_1}(x) + ... + {w_k}{f_k}(x)
w1f1(x)+...+wkfk(x),f(x)为正态分布公式。
给出x1,x2…xk,估计出均值,方差和概率w值,此处假设K=2,方便计算。
其概率分布为:

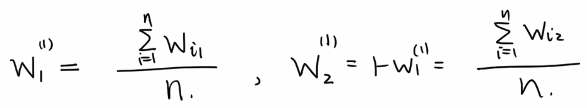
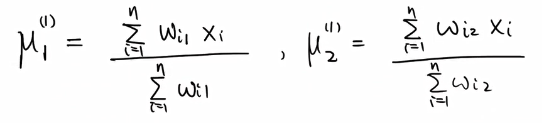
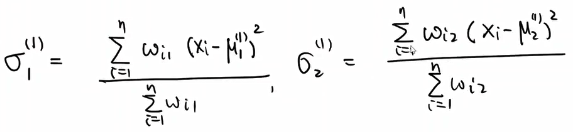
重复以上步骤即可,





















 1985
1985











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








