原学习视频跳转地址:https://www.bilibili.com/video/BV13g41157hK?p=2
本文为自学视频整理的简单笔记
目录
排序
冒泡排序
【冒泡排序的时间复杂度和数据的状态是无关的】:比较相邻的元素。如果第一个比第二个大,就交换他们两个;对每一对相邻元素做同样的工作,从开始第一对到结尾的最后一对;针对所有的元素重复以上的步骤,除了最后一个。
持续每次对越来越少的元素重复上面的步骤,直到没有任何一对数字需要比较。假设第一次要比较N次,依次往后就是N-1,N-2…,所以其时间复杂度就是一个等差数列求和O(N^2)
//交换两个数的函数swap
func swap(num1, num2 int) (int, int) {
num1 = num1 ^ num2
num2 = num1 ^ num2
num1 = num1 ^ num2
return num1, num2
}
//冒泡实现0
func bubbleSort0(arr []int) []int {
length := len(arr)
for i := 0; i < length; i++ {
for j := 0; j < length-1-i; j++ {
if arr[j] > arr[j+1] {
arr[j], arr[j+1] = swap(arr[j], arr[j+1])
}
}
}
return arr
}
//冒泡实现1
func bubbleSort(arr []int) []int {
length := len(arr)
flag := true //设置标志位
for i := 0; i < length; i++ {
for flag {
flag = false //交换之前将标志位置为FALSE
for j := 0; j < length-1-i; j++ {
if arr[j] > arr[j+1] {
arr[j], arr[j+1] = swap(arr[j], arr[j+1])
flag = true //如果发生交换操作就将标志位置为TRUE,如果没发生交换就证明当前已经排序完成
}
}
}
}
return arr
}
选择排序
【冒泡排序的时间复杂度和数据的状态是无关的】:首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
//交换两个数的函数swap
func swap(num1, num2 int) (int, int) {
num1 = num1 ^ num2
num2 = num1 ^ num2
num1 = num1 ^ num2
return num1, num2
}
//选择
func selectionSort(arr []int) []int {
length := len(arr)
for i := 0; i < length; i++ {
min := i //每次以未排序的第一个作为未排序序列的最小值
for j := i + 1; j < length; j++ {
if arr[min] > arr[j] {
min = j
}
}
arr[i], arr[min] = swap(arr[i], arr[min])
}
return arr
}
异或运算的理解:
1和0的组合运算,相同为0,不同为1;不进位的加法;性质:0和N 异或 是N,N和N 异或 是0,且满足交换律和结合律
为什么提及这个运算:在排序时我们会需要交换,我们可以用异或运算来完成不需要申请新的临时空间的交换:
假设 int a = 甲 , int b = 乙(当然两个变量得是两块独立的内存)
a = a ^ b; ------> a:甲异或乙,b:乙
b = a ^ b;-------> a:甲异或乙 ,b:甲 异或 乙 异或 乙(即等于甲)
a = a ^ b;-------> a:甲异或乙异或甲(即等于乙),b:甲
例题: 有一组数据,共有多个不同的数,有一种数出现奇数次,其他数出现偶数次,找出出现奇数次的数,要求时间O(N),空间O(1);
解:定义一个变量 a = 0,然后和所有数异或就得到那个数。
有一组数据,共有多个不同的数,有两种数出现奇数次,其他数出现偶数次,找出出现奇数次的数,要求时间O(N),空间O(1);
解:定义一个变量eor = 0(假设是a和b出现奇数次),然后和所有的数异或得到a^b,而a是不等于b的,则a和b中至少有一位是不同的(假设是第5位),因此数据可以分成两类,一类是第5位是1的数据,另一类是第5位不是1的数据,然后定义新的变量eor2 = 0去异或第5位是1的全部数据,就可以得到a或者b,后面再异或变量eor就得到另一个数。
插入排序
【时间复杂度和数据的状态有关,如一组顺序的数不用排序只需要看一下,时间复杂度O(N),而一组倒序的数排序就是O(N^2)】:在待排序的元素中,假设前面n-1(其中n>=2)个数已经是排好顺序的,现将第n个数插到前面已经排好的序列中,然后找到合适自己的位置,使得插入第n个数的这个序列也是排好顺序的。按照此法对所有元素进行插入,直到整个序列排为有序。
//插入
func insertionSort(arr []int) []int {
//从第二个数开始取值往前插入
for i := range arr {
preIndex := i - 1 //用于比较的数从排好序的最后一个开始
current := arr[i] //记录当前(未排好序的)的数
//找位置,注意这里不用交换,每一次都将比较的数往后移动覆盖后一个数,如果当前未排序的数大于等于前一个数,当前位置就是其位置
for preIndex >= 0 && arr[preIndex] > current {
arr[preIndex+1] = arr[preIndex]
preIndex -= 1
}
arr[preIndex+1] = current//将当前(未排好序的)的数放到合适的位置
}
return arr
}
二分法
用于找有序序列的某个数是否存在
用于找有序序列中大于等于NUM的最左侧的数(和上一个的区别就是这个要二分法进行到底)
用于找无序序列(相邻两个数不同)中找一个局部最小的位置:先对比0和1位置的数,0小就返回,再对比N-2和N-1的数,N-1小就返回,如果都不满足就意味着序列两边的趋势都是向下的,中间必有局部最小(拐点),然后找中间M,对比M-1和M+1,依次类推。
递归
例题:求一个数组中L位置和R位置的最大值
求中点可以用L + ((R - L) >> 1),一方面用L加上长度的一半避免了数据溢出,另一方面用 >> 运算比用除法计算快
master公式:T(N) = a*T(N/b) + O(N^d),满足这个公式的递归时间复杂度求法:
注:T(N)是总的递归求解的长度,T(N/b)是子递归求解的长度,O(N^d)是除递归外的其他的时间复杂度

归并排序(递归实现)
先将数据分成两部分进行排序,然后按下面的操作归并:
先申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
然后设定两个指针,最初位置分别为两个已经排序序列的起始位置;
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
重复步骤3直到某一指针超出序列尾,将另一序列剩下的所有元素直接复制到合并序列尾;
//数组的归并排序
func mergeSort(r []int) []int {
length := len(r)
if length <= 1 {
return r
}
num := length / 2
left := mergeSort(r[:num])//0~num-1
right := mergeSort(r[num:])//num~length-1
return merge(left, right)
}
func merge(left, right []int) (result []int) {
l, r := 0, 0
for l < len(left) && r < len(right) {
if left[l] < right[r] {
result = append(result, left[l])
l++
} else {
result = append(result, right[r])
r++
}
}
//将剩下的并上
result = append(result, left[l:]...)
result = append(result, right[r:]...)
return
}
//链表的归并排序
type ListNode struct {
Val int
Next *ListNode
}
func List_mergeSort(head *ListNode) *ListNode {
if head == nil || head.Next == nil {
return head
}
mid := getMid(head)
LeftStart := head
RightStart := mid.Next
mid.Next = nil //断开链表
return listMerge(List_mergeSort(LeftStart), List_mergeSort(RightStart))
}
func getMid(head *ListNode) *ListNode {
slow, fast := head, head //快慢指针求
for fast.Next != nil && fast.Next.Next != nil {
slow = slow.Next
fast = fast.Next.Next
}
return slow
}
func listMerge(list1, list2 *ListNode) *ListNode {
res := &ListNode{}//定义一个虚拟头结点
head := res
for list1 != nil && list2 != nil {
if list1.Val <= list2.Val {
res.Next = list1
list1 = list1.Next
} else {
res.Next = list2
list2 = list2.Next
}
res = res.Next //结果链表往后移
}
if list1 != nil {
res.Next = list1
} else {
res.Next = list2
}
return head.Next
}
.
时间复杂度是O(N * logN),对比前面的排序的时间复杂度是O(N^2),就是因为前面的每次比较行为都浪费了,而归并排序的比较行为都形成一个新的有序部分
例题:小和问题(可以用归并排序实现,如果两个数组的第一个元素相同,先拷贝右边有序数组的值,这就会导致丧失稳定性,在排序的过程中就计算小和),在一个数组中,每一个数左边比当前数小的数累加起来,叫做这个数组的小和。
例子:[1,3,4,2,5]1左边比1小的数,没有:3左边比3小的数,1:4左边比4小的数,1、3:2左边比2小的数,1:5左边比5小的数,1、3、4、2;所以小和为1+1+3+1+1+3+4+2=16
快速排序
.
1.0版本是选取数据中的最后一个数NUM,然后将前面的数划分为<=NUM和>NUM的两个区域,最后将NUM和>NUM区域的第一个数交换即可【划分的具体操作是在原数组中,arr[i]和NUM比较,如果小于NUM,arr[i]和<=区域的下一个数交换,<=区域右扩,i++;若arr[i]大于NUM,i++】
2.0版本是选取数据中的最后一个数NUM,然后将前面的数划分为<NUM、==NUM和>NUM的三个区域,最后将NUM和>NUM区域的第一个数交换即可,而1.0版本和2.0版本都存在选择的NUM在排序后是最后边的情况,这就是最坏的情况,导致其时间复杂度是O(N^2)【划分的具体操作是在原数组中,arr[i]和NUM比较,如果小于NUM,arr[i]和<区域的下一个数交换,<区域右扩,i++;若arr[i]等于NUM,i++;若arr[i]大于NUM,arr[i]和>区域的前一个数交换,i++】
3.0版本就是在数组中随机选一个数和最后一个数据交换作为NUM,然后再按2.0操作,此时好坏情况就成为概率事件,最后有长期期望可以计算到时间复杂度是O(N*logN)
//快排
func quickSort(arr []int) []int {
return quickSort_Border(arr, 0, len(arr)-1)
}
//带边界
func quickSort_Border(arr []int, L, R int) []int {
if L < R {
rand.Seed(time.Now().UnixNano())
randomNum := rand.Intn(R - L + 1) //生成0~R-L的随机数
arr[L+randomNum], arr[R] = swap(arr[L+randomNum], arr[R]) //将随机得到的基准值与最后一位交换
partitionIndex := partition(arr, L, R)
quickSort_Border(arr, L, partitionIndex[0]-1) //继续递归完成<区域的排序
quickSort_Border(arr, partitionIndex[1]+1, R) //继续递归完成>区域的排序
}
return arr
}
//分割函数,用于处理[1...r]范围的函数,默认以arr[r]做划分,划分出< = > 三个区域
//返回 =区域的左边界和右边界下标
func partition(arr []int, L, R int) []int {
less := L - 1 //<区域的最后一个数的下标
more := R //>区域的第一个数的下标
for L < more { //L表示的是当前数的位置,是还没分好区的,如果有出现和基准值一样的数分好了,则L的前一个是=区域的最后一个
if arr[L] < arr[R] { //L表示的是当前数的位置,R是设置的基准值位置
less++ //<区域扩展,并将当前的数换成<区域的最后一个数
arr[less], arr[L] = swap(arr[less], arr[L])
L++ //当前数位置右移
} else if arr[L] > arr[R] {
more--
arr[more], arr[L] = swap(arr[more], arr[L])
} else {
L++
}
}
arr[more], arr[R] = swap(arr[more], arr[R]) //将基准值和>区域的第一个数进行交换
//完成上述操作后less<区域的最后一个数的下标,more+1就是>区域的第一个数的下标
return []int{less + 1, more}
}
//交换两个数的函数swap
func swap(num1, num2 int) (int, int) {
num1 = num1 ^ num2
num2 = num1 ^ num2
num1 = num1 ^ num2
return num1, num2
}
堆结构
(插入新的数据或者删除一个数据后依旧保存堆结构的时间复杂度logN)
大根堆概念:每一个父节点都大于它的子节点,那么如何将一个数组形成一个大根堆呢?
首先我们可以理解成一棵二叉树,根节点是0,左子节点是1,右子节点是2,依次类推(形成第一层是0,第二层是1、2,第三层从左往右是3、4、5、6…),然后设置一个heapsize来代表堆的大小,而不是用数组的大小来表示堆的大小。补充一些求父节点和子节点的数组下标计算方法:
父节点的下标 = (当前节点的下标 - 1)/ 2
左子节点的下标 = 2 * 当前节点的下标 + 1
右子节点的下标 = 2 * 当前节点的下标 + 2
现在讲一下大根堆的形成过程:首先定义heapsize为0,传进来第一个数作为根节点,然后heapsize+1,之后再传进来一个数,放到左节点的位置,这时计算出父节点对应的数组下标,和父节点的值进行比较,如果比父节点的值小,则不变,如果比父节点的值大,两个节点的值进行交换,来到新位置的这个新节点要继续和其当前位置的父节点进行比较直到它的值比父节点的值要小,即可完成新数据加入堆后的最终堆的形成。
若取出最大值,如何将剩下的堆重构成大根堆?具体过程是:取出最大值后,将堆的最后一个值放到父节点的位置,然后对这个最后一个值按后面的这些方法进行调整,将index对应的元素和它的左右子节点的值进行比较,如果比它小的话,就把index对应的元素和它的左右子节点中最大的值进行交换,交换后对他的子节点也执行这个过程。
//调整大顶堆的函数
func heapify(arr []int, index, heapSize int) {
left := 2*index + 1 //左孩子节点
right := 2*index + 2 //右孩子节点
largest := index //先默认父节点为最大值
// 寻找左子节点和右子节点的最大值,当右子节点存在且右子节点的值大于左子节点的值的时候,largest才是右子节点。
if left < heapSize && arr[left] > arr[largest] {
largest = left
}
if right < heapSize && arr[right] > arr[largest] {
largest = right
}
// 把最大值下标和父节点下标进行比较来判断
if largest != index {
arr[index], arr[largest] = swap(arr[index], arr[largest]) //交换两个位置的值
//注意这里的arr[largest]变成了之前父节点的值,再次调整交换数字后的大顶堆
/*例如下面这个已经来到了index=0的位置,largest显然是2
5
15 30
10 12 20 11
交换后arr[index]为30,arr[largest]为5,index=0和largest=2不变,接下来要调整以largest=2为父节点的部分,因为它是新交换过来的
30
15 5
10 12 20 11
*/
heapify(arr, largest, heapSize)
}
}
堆排序
将一组数据转换成大根堆,然后取出根节点,将最后的那位数据换到根节点,堆数据-1,然后再重构成新的大根堆,后面重复上述操作。时间复杂度O(N*logN),空间复杂度O(1)
//堆排
func heapSort(arr []int) []int {
arrLen := len(arr)
buildMaxHeap(arr, arrLen)
for i := arrLen - 1; i >= 0; i-- {
arr[0], arr[i] = swap(arr[0], arr[i]) //最后一个节点与第一个节点交换,最后一个节点作为排好序的节点
arrLen-- //原来长度的最后一个为最大值,即排好序了,下一次调整大顶堆就不需要它了
heapify(arr, 0, arrLen)
}
return arr
}
//对数组建立一个大顶堆
func buildMaxHeap(arr []int, arrLen int) {
//从最后一个非叶子节点开始调整大根堆
//在数组中最后一个非叶子节点为length/2 - 1,从最后一个非叶子节点开始构建,即从下往上调整,从下往上能让最大(小)值元素转移到堆顶
for i := (arrLen / 2) - 1; i >= 0; i-- { // 非叶子节点的i范围从0...(n/2-1)个
heapify(arr, i, arrLen)
}
}
//调整大顶堆的函数
func heapify(arr []int, index, heapSize int) {
left := 2*index + 1 //左孩子节点
right := 2*index + 2 //右孩子节点
largest := index //先默认父节点为最大值
// 寻找左子节点和右子节点的最大值,当右子节点存在且右子节点的值大于左子节点的值的时候,largest才是右子节点。
if left < heapSize && arr[left] > arr[largest] {
largest = left
}
if right < heapSize && arr[right] > arr[largest] {
largest = right
}
// 把最大值下标和父节点下标进行比较来判断
if largest != index {
arr[index], arr[largest] = swap(arr[index], arr[largest]) //交换两个位置的值
//注意这里的arr[largest]变成了之前父节点的值,再次调整交换数字后的大顶堆
/*例如下面这个已经来到了index=0的位置,largest显然是2
5
15 30
10 12 20 11
交换后arr[index]为30,arr[largest]为5,index=0和largest=2不变,接下来要调整以largest=2为父节点的部分,因为它是新交换过来的
30
15 5
10 12 20 11
*/
heapify(arr, largest, heapSize)
}
}
//交换两个数的函数swap
func swap(num1, num2 int) (int, int) {
num1 = num1 ^ num2
num2 = num1 ^ num2
num1 = num1 ^ num2
return num1, num2
}
不基于比较的排序是根据数据状况定制的
计数排序
当输入的元素是n个0到k之间的整数时,它的运行时间是 O(n + k)。计数排序不是比较排序,排序的速度快于任何比较排序算法;
算法的步骤如下:
(1)找出待排序的数组中最大和最小的元素
(2)统计数组中每个值为i的元素出现的次数,存入数组C的第i项
(3)对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加)
(4)反向填充目标数组:将每个元素i放在新数组的第C[i]项,每放一个元素就将C[i]减去1
//计数 maxValue的设置至少要大于等于数组里的最大值
func countingSort(arr []int, maxValue int) []int {
bucketLen := maxValue + 1
bucket := make([]int, bucketLen) //bucket是0 ~ maxValue
sortedIndex := 0
length := len(arr)
for i := 0; i < length; i++ {
bucket[arr[i]] += 1 //统计出现次数
}
for j := 0; j < bucketLen; j++ {
for bucket[j] > 0 { //从桶里拿数据出来
arr[sortedIndex] = j
sortedIndex += 1
bucket[j] -= 1
}
}
return arr
}
桶排序
桶排序是计数排序的升级版,利用函数的映射关系,将输入的 N 个数据均匀的分配到K个桶中,然后桶里选择另一种合适的排序方法
基数排序(LSD)
先准备10个桶,编号0~9,从左到右根据个位数的数值,在走访数值时将它们分配至编号0到9的桶子中,然后从0号桶开始倒出数据重新串接起来,从左到右根据十位数的数值,在走访数值时将它们分配至编号0到9的桶子中,再从0号桶开始倒出数据重新串接起来,从左到右根据百位数的数值,在走访数值时将它们分配至编号0到9的桶子中,依次类推持续次数为十进制位数的个数。
LSD的基数排序适用于位数小的数列,如果位数多的话,使用MSD的效率会比较好。MSD的方式与LSD相反,是由高位数为基底开始进行分配,但在分配之后并不马上合并回一个数组中,而是在每个“桶子”中建立“子桶”,将每个桶子中的数值按照下一数位的值分配到“子桶”中。在进行完最低位数的分配后再合并回单一的数组中。
下面详细分析一下MSD的程序实现流程:
首先准备三个长度为10的数组,分别是词频数组,辅助数组,help数组
词频数组是统计一组数据中一个十进制位的的每种数字出现的次数,辅助数组就是每一位变成小于等于(累加前面的),help数组是由原数据数组(从右往左,从个位到百位)取数,再对比辅助数组得到
例如:【013 021 011 052 062】
(个位数字等于i的有几个)词频数组就是[0 2 2 1 0 0 0 0 0 0]
(个位数字小于等于i的有几个)辅助数组就是[0 2 4 5 5 5 5 5 5 5]
help数组:首先是062,个位数字小于等于2的有4个,4-1得到062在help数组的下标为3,然后辅助数组中对应2的位置减1,依次得到所有数据在桶的位置,help数组最终版:
[ 021 011 052 062 013 0 0 0 0 0]
0 1 2 3 4 5 6 7 8 9
排序算法的稳定性/排序总结
在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
(1)冒泡排序 N^2 1 稳
冒泡排序就是把小的元素往前调或者把大的元素往后调。比较是相邻的两个元素比较,交换也发生在这两个元素之间。如果两个元素相等,不用交换的;如果两个相等的元素没有相邻,那么即使通过前面的两两交换把两个相邻起来,这时候也不会交换,所以相同元素的前后顺序并没有改变,所以冒泡排序是一种稳定排序算法。
(2)选择排序 N^2 1 非稳
选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,依次类推直到第n-1个元素,第n个 元素不用选择了,因为只剩下它一个最大的元素了。那么,在一趟选择,如果当前元素比一个元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么 交换后稳定性就被破坏了,所以选择排序不是一个稳定的排序算法。
(3)插入排序 N^2 1 稳
插入排序是在一个已经有序的小序列的基础上,一次插入一个元素。比较是从有序序列的末尾开 始,也就是想要插入的元素和已经有序的最大者开始比起,如果比它大则直接插入在其后面,否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相 等的,那么插入元素把想插入的元素放在相等元素的后面。所以,相等元素的前后顺序没有改变,从原无序序列出去的顺序就是排好序后的顺序,所以插入排序是稳定的。
(4)快速排序【用的最多】(在partition时,即划分区域后进行交换元素时就不稳定了)N*logN logN 非稳
快速排序有两个方向,左边的i下标一直往右走,当a[i] <= a[center_index],其中center_index是中枢元素的数组下标,一般取为数组第0个元素。而右边的j下标一直往左走,当a[j] > a[center_index]。如果i和j都走不动了,i <= j, 交换a[i]和a[j],重复上面的过程,直到i>j。 交换a[j]和a[center_index],完成一趟快速排序。在中枢元素和a[j]交换的时候,很有可能把前面的元素的稳定性打乱,比如序列为 5 3 3 4 3 8 9 10 11, 现在中枢元素5和3(第5个元素,下标从1开始计)交换就会把元素3的稳定性打乱,所以快速排序是一个不稳定的排序算法,不稳定发生在中枢元素和a[j] 交换的时刻。
(注意:01 stable sort是牺牲时间换稳定的)
(5)归并排序 N*logN N 稳
归并排序是把序列递归地分成短序列,递归出口是短序列只有1个元素(认为直接有序)或者2个元素(1次比较和交换),然后把各个有序的段序列合并成一个有 序的长序列,不断合并直到原序列全部排好序。可以发现,在1个或2个元素时,1个元素不会交换,2个元素如果大小相等也没有人故意交换,这不会破坏稳定性。合并过程中我们可以保证如果两个当前元素相等时,我们把处在前面的序列的元素先保存在结果序列的前面,这样就保证了稳定性。所以归并排序也是稳定的排序算法。
(6)基数排序(入桶出桶都是有序的,桶也是有序的,自然基数排序就是稳定的,注意计数排序也是这样)
基数排序是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优 先级排序,最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。基数排序基于分别排序,分别收集,所以其是稳定的排序算法。
(7)堆排序(在形成大根堆的时候就已经不稳定了)N*logN 1 非稳
堆的结构是节点i的孩子为2i和2i+1节点,大顶堆要求父节点大于等于其2个子节点,小顶堆要求父节点小于等于其2个子节点。在一个长为n 的序列,堆排序的过程是从第n/2开始和其子节点共3个值选择最大(大顶堆)或者最小(小顶堆),这3个元素之间的选择当然不会破坏稳定性。但当为n /2-1, n/2-2, …1这些个父节点选择元素时,就会破坏稳定性。有可能第n/2个父节点交换把后面一个元素交换过去了,而第n/2-1个父节点把后面一个相同的元素没 有交换,那么这2个相同的元素之间的稳定性就被破坏了。所以堆排序不是稳定的排序算法。
【一般用快排,要稳就用归并,空间不够就用堆】
注:基于比较的排序时间复杂度的极限是O(NlogN),若想做到稳定性必须要有O(N)的空间复杂度,目前没有时间复杂度是O(NlogN),额外空间复杂度O(1),又稳定的排序。
链表
哈希表:增删改查的时间复杂度是O(1);有序表:增删改查的时间复杂度是O(logN)的,有序表和哈希表的区别是有序表把key按顺序组织起来
链表例题:
题1:判断一个链表是否为回文结构?(新版本要求:时间复杂度0(N),额外空间复杂度0(1))
简单版本:栈实现,将链表全部元素压入栈,然后出栈逐个比较,可以用快慢指针找中点,将后面一半元素压栈省一半空间
新版本:首先用快慢指针(快指针一次两步,慢指针一次一步)找到中点,然后让中点指向null,然后后面的元素逆序指向,然后从两头开始往中间走,取数据对比,最后再恢复单链表即可。
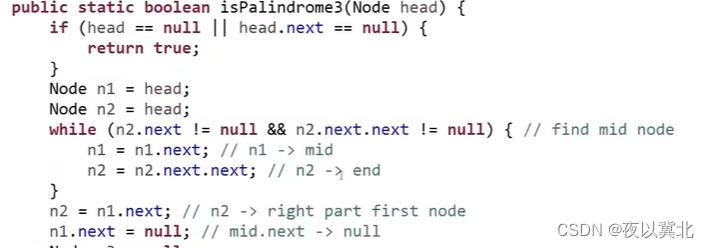
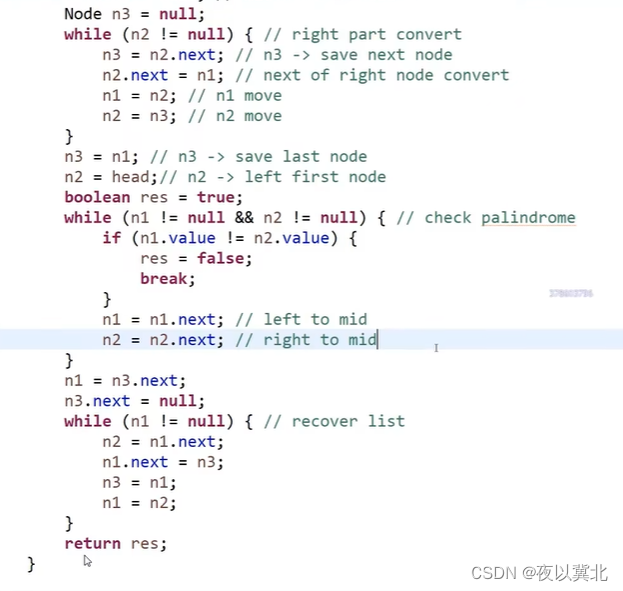
题2:将一条链表按值划分成左边小、中间相等、右边大的形式?(新版本要求:时间复杂度0(N),额外空间复杂度0(1))
简单版本:将链表的数据存放到Node数组里,然后partition,再把每一个Node串起来
新版本:定义SH、ST、EH、ET、BH和BT六个引用变量都指向NULL,然后选择出NUM,按链表的顺序比较大小,第一个小于NUM的就让SH和ST指向数据,第二个小的就让第一个数据指向第二个数据,然后ST指向第二个数据,依次类推,其他的链表也是这样形成,最后将ST指向EH,然后ET指向BH串起来即可。(注意要讨论边界问题,避免某个区域是没有值的,让最后的链表中间混了一个空指针)
题3: rand指针是单链表节点结构中新增的指针,rand可能指向链表中的任意一个节点,也可能指向nulI。给定一个由Node节点类型组成的无环单链表的头节点head,请实现一个函数完成这个链表的复制,并返回复制的新链表的头节点。(新版本要求:时间复杂度0(N),额外空间复杂度0(1))
class Node {
int value;
Node next;
Node rand;
Node(int val) {
value = val;
}
}
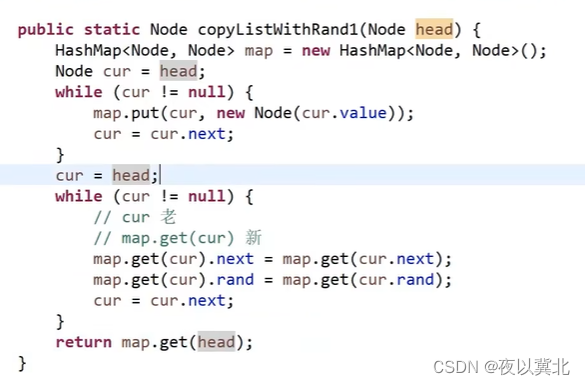
简单版本:哈希表实现,key是旧节点的地址,value是新节点的地址,第一步链表按next顺序遍历一边,对应每一个旧节点克隆一个新的节点,存放它们的地址到哈希表,第二步继续从头遍历旧链表,旧链表里每一个节点的rand和next怎么连,新链表就找它的克隆来连。
新版本:第一步按照next的顺序遍历,每遇到一个节点就复制成新节点,让旧节点指向新节点,新节点指向旧节点的next,然后再搞rand的关系,先找旧节点的rand指向谁,然后克隆的新节点的rand就指向旧节点的rand指向的下一个,这就是用位置关系替换了哈希表。
题4:两个单链表相交的一系列问题:给定两个可能有环也可能无环的单链表,头节点head1和head2。请实现一个函数,如果两个链表相交,请返回相交的第一个节点。如果不相交,返回nulI。(新版本要求:如果两个链表长度之和为N,时间复杂度请达到0(N),额外空间复杂度请达到0(1))
先判断一条单链表的入环节点?简单版本:遍历链表中的每个节点,并将它记录下来;一旦遇到了此前遍历过的节点,就可以判定链表中存在环。借助哈希表可以很方便地实现。新版本:快慢指针,相遇即有环,相遇后慢指针停在原地,快指针回到第一个节点,然后快慢指针都一步一步走,再次相遇即为第一个入环节点。
再利用上面的方法求出各链表是否有入环节点,此时就会出现三种情况:
第一种情况:两条链表都无环,先遍历两条链表,得到每条链表最后一个节点的地址,比较两个地址是否相同,相同即有相交,假设第一条遍历得到有50个节点,第二条遍历得到有30个节点,之后两条链表都设置一个标志指针指向头节点,让第一条链表的标志指针先走50-30 = 20步,然后两条链表的标志指针再一起走,第一个地址相同的即为相交节点。
第二种情况:一条链表有环,一条链表无环,必不相交。
第三种情况:两条链表有环,这种情况的相交有两种,一种是在环外相交,这种状况的入环节点的地址相同,就和之前无环的相交一样,只不过是统计节点数就遍历到第一个入环节点;另一种是在环内相交,这种状况下两条链表的入环节点都不一样,这种状况和链表不相交的情况的判断前提条件相同,下面讲一下后续区别:
在其中一个入环节点1不动的情况下,定义一个指针指向入环节点2的NEXT,然后指针以不等于入环节点1位while条件,在环内逐个对比入环节点2,如果一圈内匹配到了就是相交,返回任意一个入环节点作为相交节点即可,没匹配到就返回两条链表不相交。
二叉树
先序中序后序遍历 递归实现(略),非递归实现如下:
1.从根节点出发,沿左节点依次入栈,直到左节点为空;
2.栈顶元素出栈
3.如果出栈元素有右节点,把右节点当成开始回到步骤1,若出栈元素没有右节点,回到步骤2
4.栈空即完成
(先序是在节点入栈前访问,中序是出栈后访问)
层次遍历是先上到下,先左后右(相当于每一层从左到右),实现方法用队列:先将根节点入队,进入循环—出队一个元素以及其子节点入队(没有子节点就继续出队一个元素)
例题:
题1:如何获得一颗二叉树的最大宽度?
使用队列,层次遍历二叉树。在上一层遍历完成后,下一层的所有节点已经放到队列中,此时队列中的元素个数就是下一层的宽度。以此类推,依次遍历下一层即可求出二叉树的最大宽度。
int getWidth(BiNode head) {
if(head==null)
return 0;
int max=1;
LinkedList<BiNode>ll=new LinkedList<BiNode>();
ll.add(head);
while(true){
int len=ll.size(); //获取当前层的节点数
if(len==0) //队列空,二叉树已经遍历完
break;
while(len>0){
BiNode b=ll.poll();
len--; 出一个结点-1,为0就退循环
if(b.left!=null)
ll.add(b.left);
if(b.right!=null)
ll.add(b.right);
}
max=Math.max(max, ll.size());
}
return max;
}
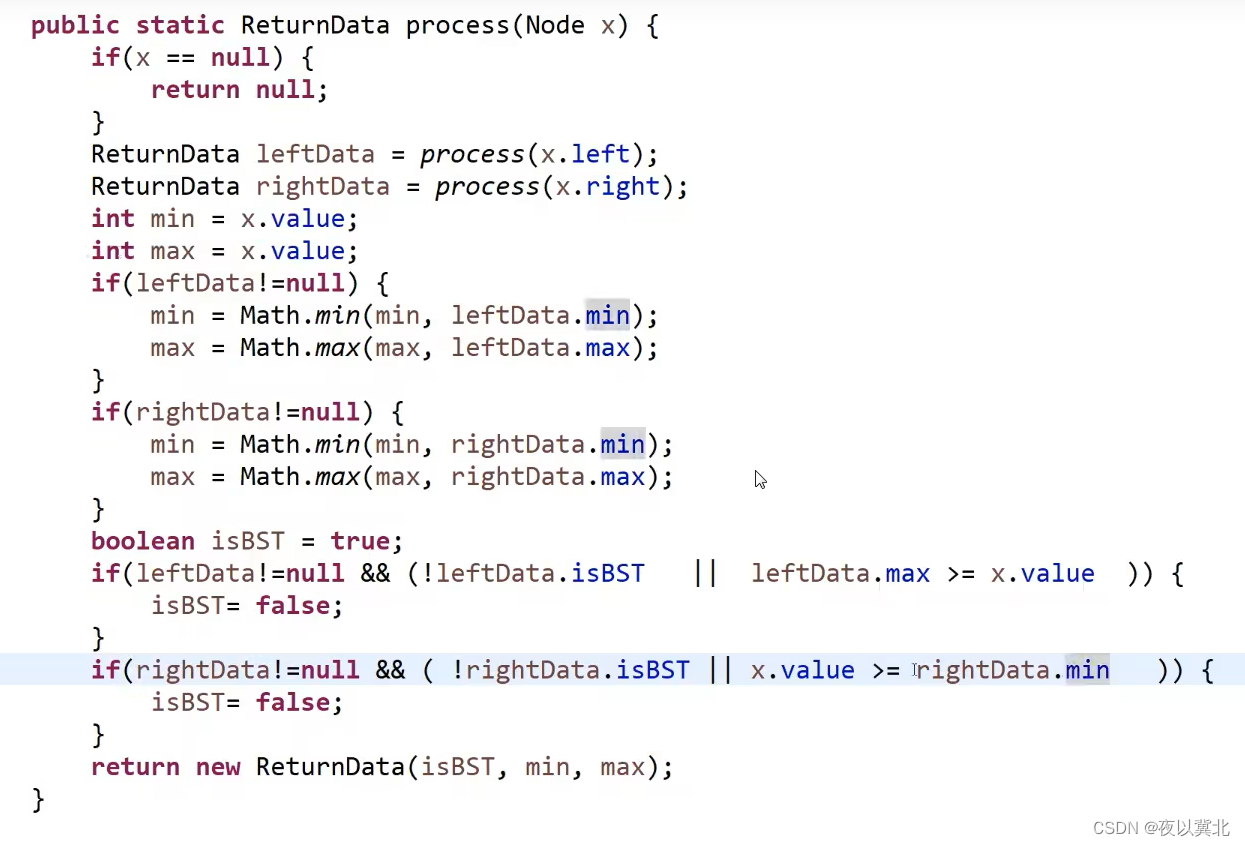
题2:如何判断一颗二叉树是否是搜索二叉树【左子树节点都比根节点小,右子树节点都比根节点大】?
中序遍历修改,打印时机变成处理时机
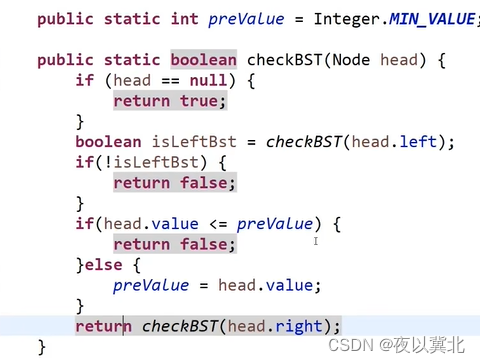
(递归套路)先拆分子条件:左子树必须是搜索二叉树,右子树必须是搜索二叉树,左数最大值小于根和右树最小值大于根
因此我们需要得到下面这些信息:左树是否为搜索?右树是否为搜索?左树最大值多少?右树最小值多少?
题3:如何判断一颗二叉树是否是完全二叉树【叶结点只出现在最下层和次下层,且最下层的叶子结点集中在树的左部】?
1)任一节点有右无左,false
2)遇到第一个左右孩子不齐,后续的节点必须是叶节点
层次遍历修改实现
题4:如何判断一颗二叉树是否是满二叉树【最大深度l,节点数N,判断N = 2^l - 1】?
题5:如何判断一颗二叉树是否是平衡二叉树?(树型DP套路:递归)
拆分子条件:左子树必须是平衡二叉树,右子树必须是平衡二叉树,左数高度-右树高度的绝对值小于等于一
因此我们需要得到下面这些信息:左树是否为平衡?右树是否为平衡?左树高度多少?右树高度多少?
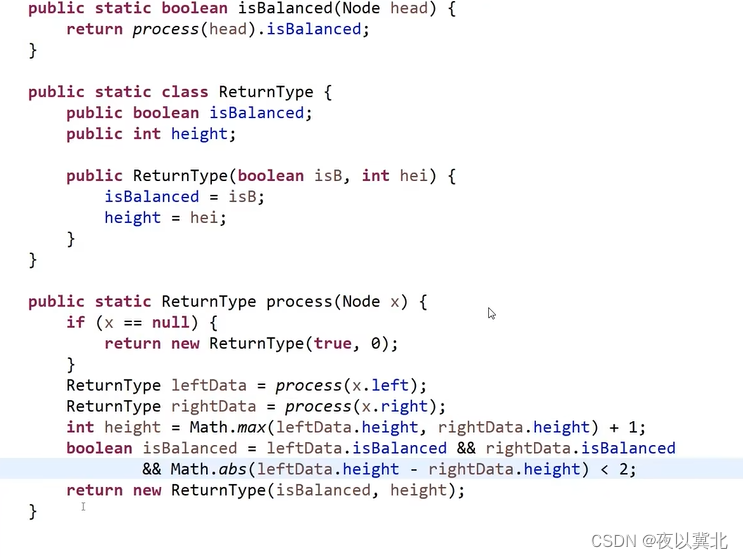
题6:给定两个二叉树的节点node1和node2,找到它们的最低公共祖先(往上第一个汇聚的点)
1)先用递归得到整个二叉树所有节点的父节点,存储起来
2)然后通过1)的记录回溯节点node1的父节点记录起来,在回溯node2的父节点时边回溯边对比node1的父节点记录,直到第一个相同的父节点即为所求
题7
public class Node {
public int value;
public Node left;
public Node right;
public Node parent;
public Node(int val) {
value = val;
}
}
按这样的节点构成的二叉树,找一个节点的后继(本意就是希望通过增加指向父节点的指针,能否将时间复杂度由之前通过中序遍历获取的O(N)降低为O(K),K表示在二叉树中节点到齐后继节点走过的距离)
第一种情况:X有右树的时候,其右子树上最左边的节点是X的后继节点
第二种情况:X无右树的时候,往上找,判断节点是否其父节点的左子节点,不是就继续往上判断父节点是否是其父节点的左子节点,直到找到符合的或者判断到根节点就结束
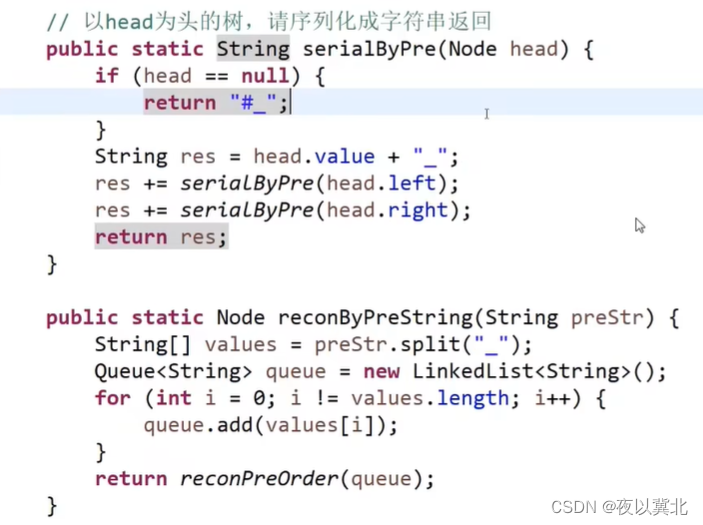
题8 二叉树的序列化和反序列化
题9 折纸问题
请把一段纸条竖着放在桌子上,然后从纸条的下边向上方对折1次,压出折痕后展开。此时折痕是凹下去的,即折痕突起的方向指向纸条的背面。如果从纸条的下边向上方连续对折2次,压出折痕后展开,此时有三条折痕,从上到下依次是下折痕、下折痕和上折痕。
给定一个输入参数N,代表纸条都从下边向上方连续对折N次。请从上到下打印所有折痕的方向。
例如:1时,打印:down N=2时,打印:down down up

图
图的难点是将图的结构表示出来,算法不会很那个,要学会将不同的图结构转化成自己熟悉的图结构,比如下面这个结构
public class Graph{
public HashMap<Integer, Node> nodes;//点集,key表示点的编号,Node表示实际的点
public HashSet<Edge> edges;//边集
public Graph(){
nodes = new HashMap<>();
edges = new HashSet<>();
}
}
public class Node{
public int value;//自己的数据项
public int in;//点的入度
public int out;//点的出度
public ArrayList<Node> nexts;//当前点发散出去的点
public ArrayList<Edge> edges;//当前点延伸出去的边
public Node(int value){
this.value = value;
in = 0;
out = 0;
nexts= new ArrayList<>();
edges = new ArrayList<>();
}
}
public class Edge{
public int weight;//边的权重
public Node from;
public Node to;
public Edge(int weight, Node from, Node to){
this.weight= weight;
this.from= from;
this.to= to;
}
}
图的宽度优先遍历
队列实现,从源节点出发依次按宽度进队列,然后弹出,每弹出一个点就把该节点的所有没进过队列的邻接点放入队列,直到队列为空
//图的宽度优先遍历
//队列实现,从源节点出发依次按宽度进队列,然后弹出,每弹出一个点就把该节点的所有没进过队列的邻接点放入队列,直到队列为空
public static void bfs(Node node){
if (node == null){
return;
}
Queue<Node> queue = new LinkedList<>();
HashSet<Node> set = new HashSet<>();//注册机制:避免无向图的环问题,只要一个节点进过队列,就在set中注册
queue.add(node);
set.add(node);
while (!queue.isEmpty()){
Node cur = queue.poll();//从队列弹出一个节点
System.out.println(cur.value);//打印节点,当然如果是面向实际的话就在这一部分写节点的相关处理即可
for (Node next : cur.nexts){
//遍历当前节点的后续节点,将其添加到队列里,注意要注册每一个进队的节点,注册过了就别再使用了
if (!set.contains(next)){
set.add(next);
queue.add(next);
}
}
}
}
}
//图的深度优先遍历
public static void dfs(Node node){
if (node == null){
return;
}
Queue<Node> stack= new stack<>();
HashSet<Node> set = new HashSet<>();//注册机制:避免无向图的环问题,只要一个节点进过队列,就在set中注册
stack.add(node);
set.add(node);
while (!stack.isEmpty()){
Node cur = stack.poll();//从栈弹出一个节点
System.out.println(cur.value);//打印节点,当然如果是面向实际的话就写当前节点的相关处理即可
for (Node next : cur.nexts){
//遍历当前节点的后续节点,将其添加到队列里,注意要注册每一个进队的节点,注册过了就别再使用了
if (!set.contains(next)){
stack.push(cur);//将当前节点重新压回栈里
stack.push(next);//将当前节点的一个邻接点压到栈里
set.add(next);
System.out.println(next.value);//打印节点,当然如果是面向实际的话就写当前节点的邻接点相关处理即可
break;//break的意义是只要将当前节点的一个邻接点压到栈中,其他邻接点先不处理
}
}
}
}
}
//拓扑排序
public static List<Node>sortedTopology(Graph graph){
//key:某一个node
//value:剩余的入度
HashMap<Node,Integer> inMap = new HashMap<>();
//入度为0的点,才能进这个队列
Queue<Node> zeroInQueue = new LinkedList<>();
for (Nodenode graph.nodes.values()){
inMap.put(node,node.in);
if (node.in == 0){
zeroInQueue.add(node);
}
}
//拓扑排序的结果,依次加入resu1t
List<Node> result new ArrayList<>();
while (!zeroInQueue.isEmpty()){
Node cur zeroInQueue.poll();
result.add(cur);
//开始去除当前节点的影响
for (Node next :cur.nexts){
inMap.put(next, inMap.get(next) - 1);
if (inMap.get(next) == 0){
zeroInQueue.add(next);
}
}
}
return result;
}
//kruskal算法(生成最小生成树,适用范围:无向图)
//将边的权值排序,然后从最小的边开始添加,如果没有形成环就添加
//下面先实现判断选择一条边之后是否会形成环,可以一开始将每一个点都当成一个小集合,然后添加边后就将点所在的集合合并,如果一条边的两个端点都在一个集合里就表示这两个点已经通过其他的边进行连接了,再添加边的话就会形成环。
//--->先实现可能用到的一些结构和接口
public static class MySets {
public HashMap<Node, List<Node>> setMap; //一个点及其对应的集合
//初始化
public MySets(List<Node> nodes) {
//一开始每一个点的集合只有自己
for(Node cur : nodes) {
List<Node> set = new ArrayList<Node>();
set.add(cur);
setMap.put(cur, set);
}
}
//是否是同一个集合
public boolean isSameSet(Node from, Node to) {
List<Node> fromSet = setMap.get(from);//将from所在的集合拿出来
List<Node> toSet = setMap.get(to);//将to所在的集合拿出来
return fromSet == toSet;//通过地址对比是否是同一个集合
}
//from所在的集合和to所在的集合合并
public void union(Node from, Node to) {
List<Node> fromSet = setMap.get(from);//将from所在的集合拿出来
List<Node> toSet = setMap.get(to);//将to所在的集合拿出来
for(Node toNode : toSet) {
fromSet.add(toNode);//将toSet中的点都加到fromSet中
setMap.put(toNode, fromSet);//把toSet中的点都指向fromSet集合
}
}
}
—>正式实现k算法
public static Set<Edge> kruskalMST(Graph graph) {
UnionFind unionFind = new UnionFind();//生成一个并查集
unionFind.makeSets(graph.nodes.values());//初始化
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
for(Edge edge : graph.edges) {//M条边
priorityQueue.add(edge);//O(logM)
}
Set<Edge>result = new Hashset<>();
whi1e(!priorityQueue.isEmpty()) {//M条边
Edge edge priorityQueue.poll();//O(logM)
if (lumionFind.isSameSet(edge.from, edge.to)){//O(1)
result.add(edge);
unionFind.union(edge.from, edge.to);
}
}
return result;
}
//prim算法
public static Set<Edge> primMST(Graph graph) {
//解锁的边进入小根堆
PriorityQueue<Edge> priorityQueue = new PriorityQueue<>(new EdgeComparator());
HashSet<Node> set = new HashSet<>();
Set<Edge> result = new HashSet<>();//依次挑选的边放在result中
for (Node node : graph.nodes.value()) {//随便选一个点,这个for循环是为了处理森林问题
if (!set.contains(node )){
set.add(node);
for (Edge edge : node.edges) {//由一个点解锁其所有与其相连的边
priorityQueue.add(edge);
}
}
while (!priorityQueue.isEmpty()) {
Edge edge = priorityQueue.poll();//弹出权值最小的边
Node toNode = edge.to; //可能的一个新点
if (!set.contains(toNode)){ //不含有的时候就是新点
set.add(toNode);
result.add(toNode);
for (Edge nextEdge : toNode.edges) {//下一个点解锁其所有与其相连的边
priorityQueue.add(edge);
}
}
}
}
return result;
}
//dijkstra算法
public static HashMap<Node, Integer>dijkstral(Node head)
//从head出发到所有点的最小距离
//key:从head出发到达key
//value:从head出发到达key的最小距离
//如果在表中,没有T的记录,含义是从head出发到T这个点的距离为正无穷
HashMap<Node, Integer> distanceMap new HashMap<>();
distanceMap.put(head, 0);//一开始就是到自己的距离为0
//已经求过距离的节点,存在selectedNodes中,以后再也不碰
HashSet<Node> selectedNodes = new HashSet<>();
//找到最小的距离,选过的点不要
Node minNode = getMinDistanceAndUnseLectedNode(distanceMap, selectedNodes);
while (minNode != null){
int distance = distanceMap.get(minNode);
for (Edge edge : minNode.edges){
Node toNode = edge.to;
if (!distanceMap.containsKey(toNode)){
distanceMap.put(toNode,distance edge.weight);
}
distanceMap.put(edge.to, Math.min(distanceMap.get(toNode), distance + edge.weight));
)
selectedNodes.add(minNode);
minNode = getMinDistanceAndUnseLectedNode(distanceMap, selectedNodes);
)
return distanceMap;
}
public static Node getMinDistanceAndUnselectedNode(
HashMap<Node, Integer> distanceMap,
HashSet<Node> touchedNodes) {
Node minNode null;
int minDistance = Integer.MAX_VALUE;
for (Entry<Node, Integer> entry : distanceMap.entrySet()){
Node node entry.getKey();
int distance entry.getvalue();
if (ItouchedNodes.contains(node) && distance minDistance){
minNode = node;
minDistance = distance;
}
}
return minNode;
}
//改进的d算法是利用堆来替换上述的遍历
前缀树(字典树)可按如下定义:
public static class TrieTree {
public int pass;//经过一个点就+1
public int end;//作为一个字符的结尾就+1,注意每个点都会有一个pass和一个end,如下图
public TrieNode[] nexts;//如果字符种类不只是26个字母,可以用哈希表节省空间HashMap<Char, Node> nexts;
public TrieNode() {
//初始化每个节点的p和e
pass = 0;
end = 0;
nexts = new TrieNode[26];//每个节点都可以延伸26个子节点
}
}
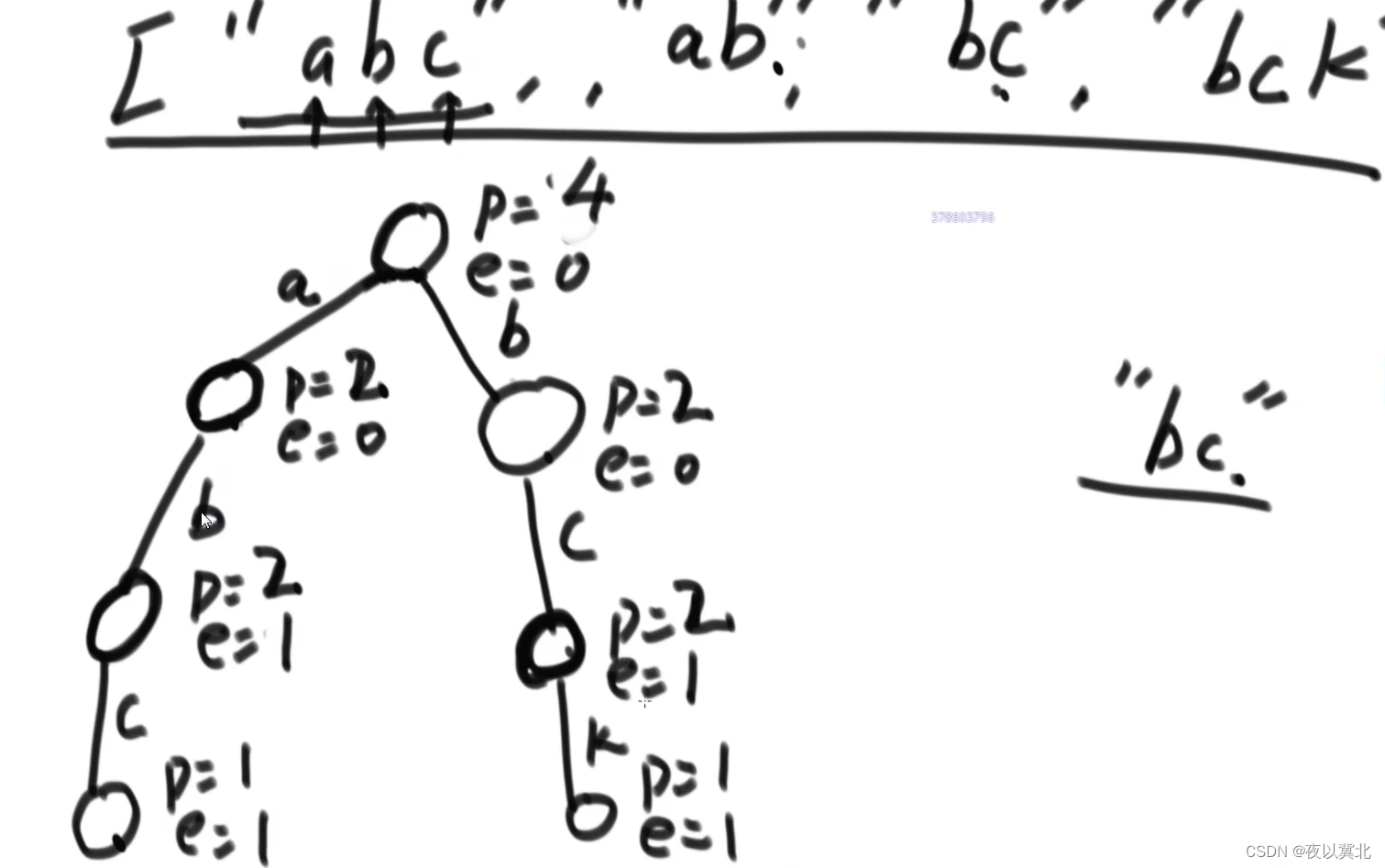
//--->插入操作
//每一个节点的pass表示有多少个节点以根到当前节点的字母组合作为前缀,比如根节点的p就表示有多少个字符串是以空作为前缀加入到当前前缀树的
private TrieNode root;
public Trie() {
root = new TrieNode();
}
public void insert(String word) {
if (word == null) {
return;
}
char[] chs = word.toCharArray();
TrieNode node = root;//node是我们用来处理节点的对象,从根节点出发,然后根节点的pass+1
node.pass++;
int index = 0;//作为查询字母的一个简化变量
for (int i = 0; i < chs.length; i++) {
index = chs[i] - 'a';
if (node.nexts[index] == null) {//如果子节点还没有新建,就新建一个
node.nexts[index] = new TrieNode();
}
node = node.nexts[index];//node移到下一个节点
node.pass++;//下一个节点的p++
}
node.end++;//直到字符串的前缀树生成到最后一个节点时,最后一个节点的end++
}
//--->查询操作,查字符和查前缀
public int search(String word) {
if (word == null) {
return;
}
char[] chs = word.toCharArray();
TrieNode node = root;//node是我们用来处理节点的对象,从根节点出发
int index = 0;//作为查询字母的一个简化变量
for (int i = 0; i < chs.length; i++) {
index = chs[i] - 'a';
if (node.nexts[index] == null) {
return 0;
}
node = node.nexts[index];//node移到下一个节点
}
return node.end;
}
public int prefixNumber(String pre) {
if (pre == null) {
return;
}
char[] chs = pre.toCharArray();
TrieNode node = root;//node是我们用来处理节点的对象,从根节点出发
int index = 0;//作为查询字母的一个简化变量
for (int i = 0; i < chs.length; i++) {
index = chs[i] - 'a';
if (node.nexts[index] == null) {
return 0;
}
node = node.nexts[index];//node移到下一个节点
}
return node.pass;
}
//--->删除操作
public int delete(String word) {
if (search(word) != 0) {
char[] chs = word.toCharArray();
TrieNode node = root;//node是我们用来处理节点的对象,从根节点出发
node.pass--;
int index = 0;//作为查询字母的一个简化变量
for (int i = 0; i < chs.length; i++) {
index = chs[i] - 'a';
if (--node.nexts[index].pass == 0) {//然后最后的pass已经删除0了,就删掉那个节点
//而C++要遍历到底去析构
node.nexts[index] = null;
return;
}
node = node.nexts[index];//node移到下一个节点
}
node.end;--
}
}
贪心策略
- 最优装载问题:每次装价值最大的物品即可;
- 活动安排问题(属于安排策略,竞争某一公共资源问题):使得剩余的时间最大化,先安排最早结束的活动;
- 最小生成树问题(MST问题):Kruskal算法、prim算法、单源最短路径问题(dijkstra算法);
例1:有n个项目,每个项目花费为c[i],收益为p[i],最多可做k个项目,m是初始资金,每做完一个项目的收益可以立即支持下一个项目的投资,求最后获得的最大钱数。
先用一个小根堆按照花费大小将全部项目排列起来,根据现有的资金从小根堆中取出最小开销的几个项目,然后再用一个大根堆按照收益的大小将取出的项目进行排列,获得收益最大的项目,然后累加初始资金到小根堆再取出一些可完成的项目,加入大根堆再排列,再取收益最大的项目来完成,以此类推。
例2:一条金条切分时,需要花费与金条长度相同的钱数,比如长度为30的金条无论切分成几份都要花费30块钱,现有一长度为60的金条,需要分成长度为5,8,9,11,12,18的六份,问怎么分代价最小?
先用小根堆按照花费的大小排序,然后每次取出两个最小的值累加起来,再把这个累计的一个值放回到小根堆排序(哈夫曼编码),重复此操作直到小根堆只有一个数
补充:N皇后问题
public static int num1(int n) {
if (n < 1) {
return 0;
}
int[] record = new int[n];//下标n表示第n行,record[n]表示列数
return process1(0, record, n);
}
//record〔0..1-1]表示之前的行,放了的皇后位置
//n代表整体一共有多少行
//返回值是,摆完所有的皇后,合理的摆法有多少种
public static int process1(int i,int[] record,int n){
if(i == n) {//终止行
return 1;
}
int res = 0;
for(int j = 0;j < n; j++) {//当前行在i行,尝试i行所有的列->j
//当前1行的里后,放在列,会不会和之前(0...i-1)的皇后,共行共列或者共斜线,
//如果是,认为无效
//如果不是,认为有效
//回溯递归:逐个去尝试的过程,就是先在第一行选一个位置,然后到第二行选一个位置,依次类推直到最后一行选好位置,然后回退到倒数第二行,选择下一个有效的位置再到最后一行选位置
if (isValid(record,i,j)) {
record[i] = j;
res += process1(i + 1, record, n);
}
}
return res;
}
//record[0...i-1]你需要看,record[i...]不需要看
//返回i行皇后,放在了j列,是否有效
//判断是否同列?对角是等腰三角形,两个皇后的行差数值等于列差数值
public static boolean isValid(int[] record, int i, int j) {
for(int k = 0; k < 1; k++)(//之前的某个k行的皇后
if (j == record[k] || Math.abs(record[k] - j) == Math.abs(i - k)) {
return false;
}
}
return true;
}
汉诺塔问题
其实就是三个步骤:
一开始有from、to、other三个地方,n个圆盘从from移动到to上
第一步:n-1个圆盘从from移动到other上
第二步:第n个圆盘从from移动到to上
第三步:n-1个圆盘从other移动到to上
下面实现这个移动的函数(整体移动就是递归实现)
public static void hanoi(int n) {
if (n > 0) {
func(n, "左", "右", "中");
}
}
public static void func(int i, String start, String end, String other) {
if (i == 1) {
System.out.println("Move 1 from " + start + " to" + end);
} else {
funn(i - 1, start, other, end);//注意这里的参数要按上述文字描述的过程给
System.out.println("Move " + i + "from " + start + " to" + end);
func(i - 1, other, end, start);
}
}
如何得到一个字符串的全部子序列
public static void printAllSubsquence(String str) {
char[]chs str.toCharArray();
process(chs,0);
}
//当前来到i位置,要和不要,选择一条路
//之前的选择形成的结果就是str,就是在原字符串的数组改
public static void process(char[] str, int i){
if (i == str.length) {
System.out.println(String.vaLueof(str));
return;
}
process(str, i + 1);//要当前字符的路
char tmp str[i];
str[i] = 0;
process(str,i + 1);//不要当前字符的路
str[i] = tmp;
}
如何得到一个字符串的全排列?
//str[i..]范围上,所有的字符,都可以在i位置上,后续都去尝试
//str[0.,i-1]范围上,是之前做的选择
//请把所有的字符串形成的全排列,加入到res里去
public static void process(char[] str,int i,ArrayList<String> res) {
if (i == str.length){
res.add(String.valueof(str));
}
boolean[] visit = new boolean[26];//visit[0 1..25]
for (int j = i; j < str.length; j++){
if (!visit[str[j] - 'a']) {
visit[str[j] - 'a'] = true;
swap(str, i, j);
process(str, i+1, res);
swap(str, i, j);
}
}
}
//每个人轮流从最左或者最右拿纸牌,f表示先手能获得的最高分数,s表示后手能获得的最高分数
public static int win1(int[] arr) {
if (arr == null || arr.length == 0) {
return 0;
}
return Math.max(f(arr, 0, length - 1), s(arr, 0, length - 1));
}
public static int f(int[] arr, int i, int j) {
if (i == j) {
return arr[i];
}
return Math.max(arr[i] + s(arr, i + 1, j), arr[j] + s(arr, i, j - 1));
}
public static int s(int[] arr, int i, int j) {
if (i == j) {
return 0;
}
return Math.max(f(arr, i + 1, j), f(arr, i, j - 1));
}
一个栈用递归实现逆序
需要一个辅助函数:将一个栈的栈底元素返回,然后将上面的元素按原来的顺序覆盖栈底元素
public static int f(Stack<Integer> stack) {
int result = stack.pop();
if (stack.empty()) {
return result;
} else {
int last = f(stack);
stack.push(result);
return last;
}
}
public static int reverse(Stack<Integer> stack) {
int result = stack.pop();
if (stack.empty()) {
return result;
}
int i = f(stack);//调用上面的辅助函数实现
reverse(stack);
stack.push(i);
}
有两个长度为N的数组weight和value,给定一个固定重量bag,要求在重量范围以内装入的最大价值是多少?
//i位置之后的货物自由选择,形成的最大价值返同
//重量水远不要超过bag
//之前做的决定,所达到的重量,a1 readyweight
public static int process1(int[]weights, int[]values, int i, int alreadyweight, int bag) {
if (alreadyweight > bag) {
return 0;
}
if (i == weights.length) {
return 0;
}
return Math.max(
process1(weights, values, i + 1, alreadyweight, bag),
values[i] + process1(weights, values, i + 1, alreadyweight + weights[i], bag)
);
}
哈希函数和哈希表
输入域无限,输出域有限,对于不同输入所产生的结果有离散型和均匀性
例1:假设有40亿个数,给你1GB空间,请找出出现次数最多的那个数字。
考虑用哈希表统计次数,key设为数字种类,value设置为对应种类出现的次数,首先最好的情况是40亿个都是一样的数字,这时哈希表就只有一条记录,最坏的情况是有40亿个不同的数字,暂且不算哈希表搜索时的使用空间,按一个数字4字节,一条记录就是8字节,40亿条记录就是32GB,所以不可以直接就用上哈希表记录。
1.先用哈希函数计算得到新的离散且均匀分布的一组哈希值,目的是为了打散集中的数字,我们的本意就是想通过划分成多个文件进行处理的,如果数字有规律就会出现有些文件的数字种类偏少,有些文件的数字种类偏多(比如全部数字对100求模都是12,不就全塞到12号文件了?这和直接用哈希表统一就没区别了)
2.再将每一个元素的哈希值对100求模,同时按照0~99命名建立一百个文件。按照模值与文件名对应的方式,将40亿个数字分别在一百个文件里面进行统计,每一个文件中包含的数字种类是差不多的,也就是说每个文件的大小应该是差不多的。
3.然后求出100个文件里面最大的数字,再进行比较,从而得到最大的数字。
哈希表(key,value) 就是把Key通过一个固定的算法函数转换成一个整型数字,然后就将该数字对数组长度进行取余,取余结果就当作数组的下标,将value存储在以该数字为下标的数组空间里,哈希表在使用的时候增删改查是O(1),但是理论上还是O(logN)的。
例2:设计一种结构,要求功能:insert(key):将某个key加入到该结构时,做到不重复加入,delete(key):将原本在结构中的某个key删除,getRandom():等概率随机返回结构中的某个key,要求功能实现都是O(1)。
public static class Pool<K>{
private HashMap<K, Integer> keyIndexMap;
private HashMap<Integer, K> indexKeyMap;
private int size;
//初始化
public Pool(){
this.keyIndexMap = new HashMap<K,Integer>();
this.indexKeyMap = new HashMap<Integer,K>();
this.size = 0;
}
public void insert(K key){
if (!this.keyIndexMap.containsKey(key)) {
this.keyIndexMap.put(key,this.size);
this.indexKeyMap.put(this.size++,key);
}
}
public K getRandom(){
if (this.size == 0) {
return null;
}
int randomIndex = (int) (Math.random() * this.size);//生成随机数的函数
return this.indexKeyMap.get(randomIndex);
}
public void delete(K key){
if (this.keyIndexMap.containsKey(key)) {
int deleteIndex = this.keyIndexMap.get(key);
int lastIndex = --this.size;
K lastKey = this.indexKeyMap.get(lastIndex);//把最后一个key拿出来
this.keyIndexMap.put(lastKey, deleteIndex);//将最后一条记录补充到上面删除的位置中,维持哈希表的记录索引是连续的
this.indexKeyMap.put(deleteIndex, lastKey);
this.keyIndexMap.remove(key);
this.indexKeyMap.remove(lastIndex);
}
}
布隆过滤器(使用条件:允许有一定的误判时,可极大节省内存空间)
比特状态位信息,一个int型占4个字节,即4*8=32个比特状态位
int[] arr = new int[10];//长度为10的int型数组表示长度为320比特的数组
int i = 156;//取出第156位的比特状态
int numIndex = i / 32;//一个int型的数是32比特,这一步就是找156比特位在哪个数的位置
int bitIndex = i % 32;//偏移量
int s = ( (arr[numIndex] >> bitIndex ) ) & 1;//获取比特位信息
arr[numIndex] = arr[numIndex] | (1 << (bitIndex))//将156位比特位的状态修改成1
arr[numIndex] = arr[numIndex] & (~(1 << (bitIndex)))//将156位比特位的状态修改成0
具体应用时,假设有一组URL黑名单,设定k个哈希函数,长度为m的格子段;单个URL通过k个哈希函数获得k个哈希值,然后每个哈希值对m求模,获得k个可能不同的格子,在m长度的格子段中描黑对应的格子,这个格子段就是最后记录的东西。
下面讲一下k和m对失误率的影响:
1.m当然是越大越好,长度过小会导致格子有可能涂满,最差的情况就是全部URL都涂满了,查谁都是黑名单,当然过大的话就会浪费空间了,毕竟0.00001%和0.000001%的失误率差不多;
2.k过小时只描黑较少的格子,和其他URL区分不大,k过大时描黑较多格子,有可能会占满格子导致区分不大,所以k需要根据m来决定。
n = 样本量 p = 失误率


实际失误率计算公式如下,下面的k和m都要套上面计算得到的值

三.一致性哈希原理
普通 hash 算法会出现一些缺陷:如果服务器已经不能满足缓存需求,就需要增加服务器数量,假设我们增加了一台缓存服务器,此时如果仍然是对服务器数量求模来对同一张图片进行缓存,那么这张图片所在的服务器编号必定与原来服务器(假设原来是三台服务器)时所在的服务器编号不同,因为除数由3变为了4,最终导致所有缓存的位置都要发生改变,也就是说,当服务器数量发生改变时,所有缓存在一定时间内是失效的,当应用无法从缓存中获取数据时,则会向后端服务器请求数据,后端服务器将会承受巨大的压力,整个系统很有可能被压垮。
一致性哈希算法是对 2^32 取模,具体步骤如下:
1.将整个哈希值空间按照顺时针方向组织成一个虚拟的圆环,称为 Hash 环;
2.将各个服务器使用 Hash 函数进行哈希,具体可以选择服务器的IP或主机名作为关键字进行哈希计算得到每台机器在哈希环上的位置;
3.将数据key使用相同Hash函数计算出哈希值,并确定此数据在环上的位置,从此位置沿环顺时针寻找,第一台遇到的服务器就是其应该定位到的服务器。
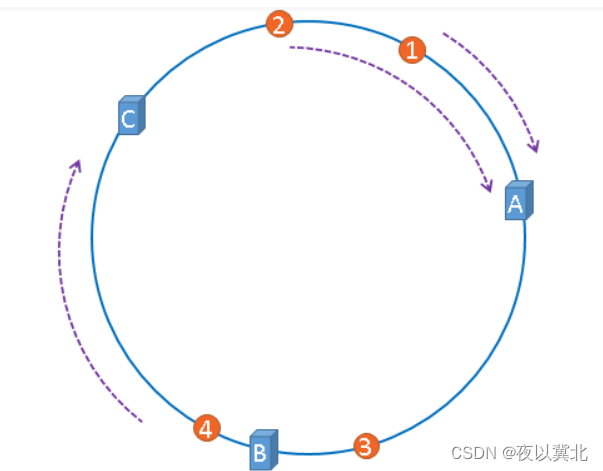
一致性哈希算法对于节点的增减都只需重定位环空间中的一小部分数据,只有部分缓存会失效,不至于将所有压力都在同一时间集中到后端服务器上,具有较好的容错性和可扩展性;但是有这么一种情况:当服务器计算得到的哈希值求模后得到的数值接近时,就会导致哈希环倾斜,解决办法是引入了虚拟节点机制,即对每一个服务节点计算多个哈希,每个计算结果位置都放置一个此服务节点,称为虚拟节点,一个实际物理节点可以对应多个虚拟节点,虚拟节点越多,hash环上的节点就越多,缓存被均匀分布的概率就越大,hash环倾斜所带来的影响就越小,同时数据定位算法不变,只是多了一步虚拟节点到实际节点的映射,具体做法可以在服务器ip或主机名的后面增加编号来实现。
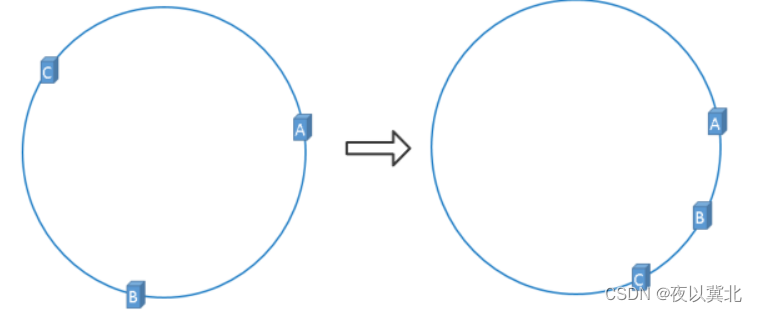
并查集
例题:一个矩阵中只有0和1两种值,每个位置都可以和自己的上、下、左、右四个位置相连,如果有一片1连在一起,这个部分叫做一个岛,求一个矩阵中有多少个岛?如何设计一个并行算法解决这个问题
001010
111010
100100
000000
这个矩阵中有三个岛
function islandCount(arr){
if (!arr || arr.length == 0) {
return;
};
let N = arr.length, M = arr[0].length, res = 0;
for(let i = 0; i < N; i++){
for(let j = 0; j < M; j++){
if (arr[i][j] === 1) {
++res;
infect(arr,i,j,N,M);
}
}
}
return res;
}
function infect(arr,i,j,N,M){
if (i < 0 || j < 0 || i >= N || j >= M || arr[i][j] !== 1) {
return;
};
arr[i][j] = 2;//一上来就把1改成2,避免后续往上又调用
infect(arr,i,j-1,N,M);
infect(arr,i+1,j,N,M);
infect(arr,i,j+1,N,M);
infect(arr,i-1,j,N,M);
}
接下来先说明一下并查集的结构,并查集:往上指的图
public static class Element<V> {
public V value;//将用户传进来的数据再封装一层
public Element(V value) {
this.value = value;
}
}
public static class UnionFindSet<V> {
public HashMap<V,Element<V>> elementMap;//第一张表是用户数据和其对应的封装的表,也可以理解成注册数据
public HashMap<Element<V>,Element<V>> fatherMap;//第二张表表示一个元素和其父元素的表,key某个元素,value该元素的父元素
public HashMap<Element<V>,Integer> sizeMap;//第三张表表示一个数据集合和其包含的元素个数的表,key某个集合的代表元素,value该集合的大小
public UnionFindSet(List<V> list){
elementMap = new HashMap<>();
fatherMap = new HashMap<>();
sizeMap = new HashMap<>();
for (V value : list){
Element<V> element = new Element<V>;
elementMap.put(value,element);
fatherMap.put(element,element);//初始化时每个元素对应的集合中,集合的代表元素就是自己
sizeMap.put(element,1);
}
}
//给定一个ele,往上一直找,把代表元素返回
private Element<V> findHead(Element<V> element) {
Stack<Element<v>> path = new stack<>();
while (element |= fatherMop.get(element)) {
path.push(eloment);//往上走的时候一边走一边将元素加到栈内
element = fatherMap.get(element);
}
while (!path.isEmpty()) {
fatherMap.put(path.pop(), element);//这一步是优化结构,将后续的大串元素直接接到代表元素的后面,这是为了如果将来还要查询这些元素的代表元素,就可以直接一步找到,不用走这么长的串
}
return element;//返回代表元素
}
public boolean isSameSet(V a,V b){
if(elementMap.containsKey(a) && elementMap.containsKey(b)) {
return findHead(elementMap.get(a)) == findHead(elementMap.get(b));
}
return false;
}
public void union(V a, V b){
if(elementMap.containsKey(a) && elementMap.containsKey(b)) {
Element<V> aF = findHead(elementMap.get(a));
Element<V> bF = findHead(elementMap.get(b));
if (aF != bF) {
Element<V> big = sizeMap.get(aF) >= sizeMap.get(bF) ? aF : bF;
Element<V> small = big == aF ? bF : aF;
fatherMap.put(small, big);//将小的集合接到大集合的代表元素之后,注意不是大集合的底部元素
sizeMap.put(big, sizeMap.get(aF) + sizeMap.get(bF));
sizeMap.remove(small);
}
}
}
回到岛问题的第二问上,如何并行解决?
假设有a、b、c、d四块区域等待合并时(四块区域原本都是一个),从中选出一个(如a),对他的边界进行判断,如果边界上有节点是2,而与它相邻区域的节点也是2,说明它们应该是联通在一起的,此时可以执行unionSet,将两个区域合并(合并ac),此时岛的数量 - 1;继续遍历a的边界,发现b可以c联通,并且bc不在同一个集合,继续合并,岛的数量 - 1;继续遍历,发现b可以d联通,并且bd不在同一个集合,继续合并,岛的数量 - 1;继续遍历,发现a可以d联通,但ad在同一个集合,不需要合并,岛的数量为1。
因此思路总结:第一步计算两部分岛的数量并收集边界信息;第二步利用并查集实现减少岛的过程。如果有多个CPU或计算单元,可以将整个输入域划分为多个部分,对每个部分计算岛的数量并收集4个边界的信息;在合并时依然利用并查集实现任意两个相邻部分的合并。
线段树(区间修改树)
线段树结构,对外提供三个接口:
- add方法—>L到R范围内所有数字加一个数V;
- update方法—>L到R范围内所有数字修改成一个数V;
- getSum方法—>返回L到R范围内所有数字的累加和;
对于一个是2的幂次长度(假设为N)的区域,就可以用一颗满二叉树存储区间信息(例如1~8,如下图所示),此时所需要的空间就是2N-1,用2N的空间即可,这种情况是最省空间的,如果刚好是2的幂次长度加一(假设为M)的区域,在底层左边M-1个数往上构建二叉树就刚好是一颗满二叉树,而剩余的右边一个要和左边一起构建满二叉树的话,就需要补很多的节点,令N=M-1,即左边最底层的节点数为N,右边也要补零扩充到N,这样构建的满二叉树就需要空间的大小是4N-1(用数组方式存储),这种情况是最浪费空间的
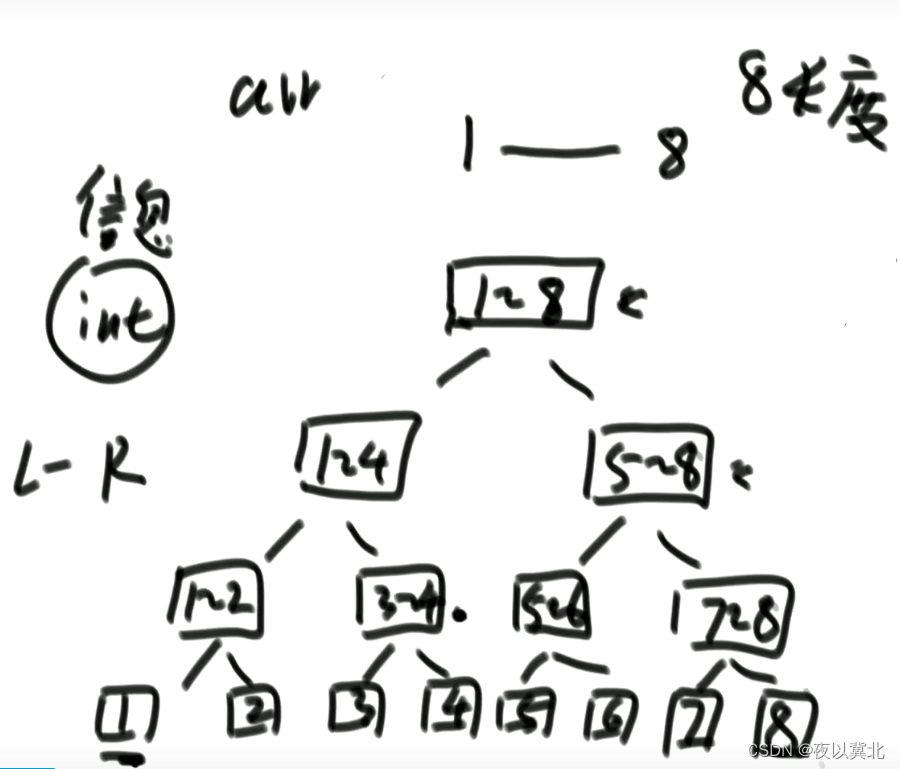
//!!!!!!!!!!这是伪代码!!!!!!!!!!
arr := [4 6 2 6 8 5 2]
Sum := 4*len(arr)+1长度的数组,然后Sum[0]位置弃置不用,从1开始,这样做的目的就是为了后面算Sum下标时用位运算代替乘法运算
//构建累加和数组Sum的函数,index表示L~R范围在Sum数组的下标
func bulid(L,R,index int) {
if L == R {
Sum[index] = arr[l]
return
} else {
mid := (1 + R) >> 1
build(1,mid,index << 1)
build(mid+1,R,index << 1 | 1)
pushUp(index)//汇总
}
}
func pushUp(index int) {
Sum[index] = sum[index << 1] + sun[index << 1 | 1]
}
对于线段树累加和,找到线段树对应数组的值
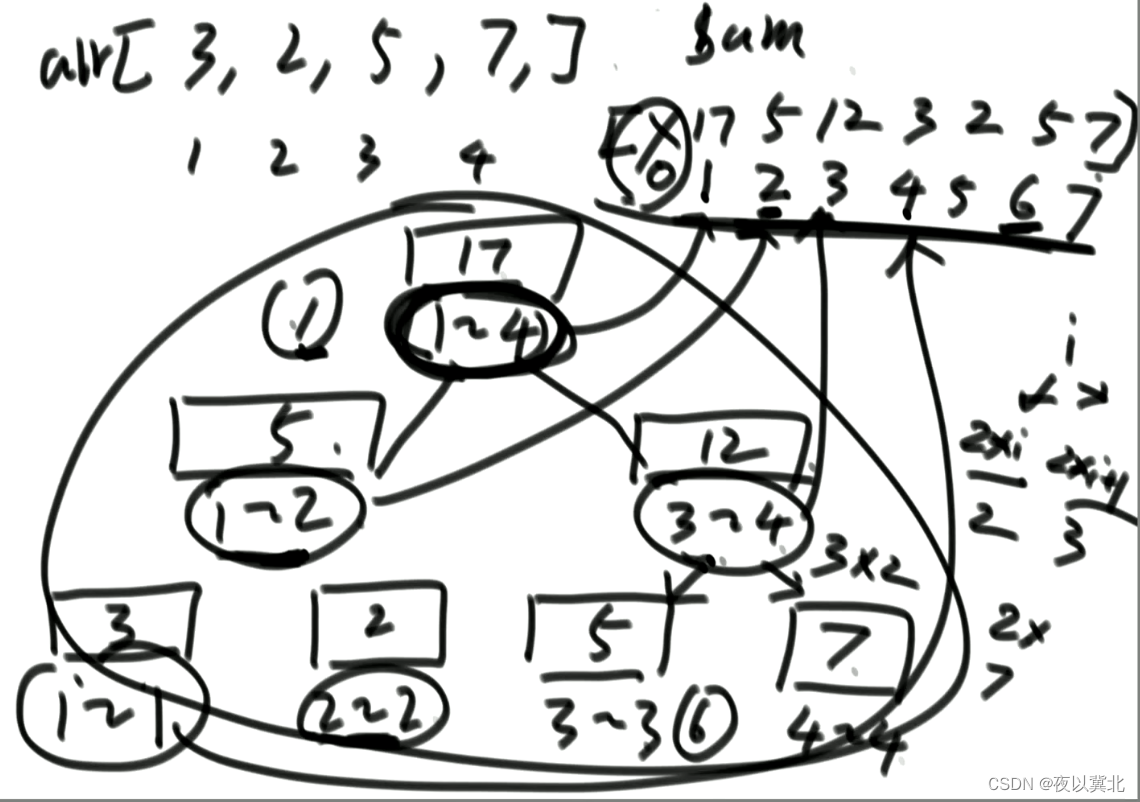
对一个区间内全部数都加上V,例如1-6上全部数加4,此1~6就成为一个任务,
先下发到根节点1-8,可得任务范围1-6不能全部包括1-8,然后将任务下达给子节点;
对比1-6和1-4,任务范围1-6全部包括1-4,则这边不再把任务下发,并将lazy数组中1-4的位置填上要求的加数4;对比1-6和5-8可得任务范围1-6不能全部包括5-8,下发任务;
对比5-6和1-6,任务范围1-6全部包括5-6,这边不把任务下发,并将lazy数组中5-6的位置填上要求的加数4;对比7-8和1-6,任务不下发
那么怎么破坏懒机制?
即又来了一个新的任务(比如说在1-5加8),和上面类似的操作来到1-4时,发现lazy数组里1-4是有值的,就让lazy数组将之前的+4任务下发给1-2和3-4,即将lazy数组的1-2和3-4的位置填上4,然后1-4的位置清零后改成8,右边同理,都是遇到之前的lazy数组有值时就将之前的任务下发到lazy的子节点,然后将当前的待加数填入lazy数组的对应位置
//!!!!!!!!!!这是伪代码!!!!!!!!!!
//L和R表示任务的范围,C表示待加的数,l和r表示来到的实际范围,index表示l和r对应的lazy数组或者sum数组的下标索引
func add(L,R,C,l,r,index int) {
if L < l && r > R {//任务范围大于实际范围
sum[index] += C * (r-l+1)
lazy[index] += C //懒住
return
}
//任务范围并没有全包括当前实际范围,懒不住就要把所有懒任务下发
mid = (1+r)>>1
pushDown(index, mid -l +1,r-mid)
//左孩子是否需要接任务
if(L <= mid) {
add(L,R,C,1,mid,index<<1)
}
//右孩子是否需要接任务
if(R > mid) {
add(L,R,C,mid+1,r,index<<1 | 1)
}
//左右孩子做完任务,更新父范围的sum
pushUp[index]
}
//下发任务函数,ln表示左子树的元素个数,rn表示右子树的元素个数
func pushDown(index,ln,rn) {
/*update先不看
if update[index] {
update[index << 1] = true//左子节点
update[index << 1 | 1]//右子节点
change[index << 1] = true//左子节点
change[index << 1 | 1]//右子节点
lazy[index << 1] = true//左子节点
lazy[index << 1 | 1]//右子节点
sum[index << 1] = true//左子节点
sum[index << 1 | 1]//右子节点
update[index] = false
}
*/
if lazy[index] != 0 {
lazy[index << 1] += lazy[index]//更新lazy[index]的左子节点
sum[index << 1] += lazy[index] * ln//左孩子累加,然后总和累加
lazy[index << 1 | 1] += lazy[index]//更新lazy[index]的右子节点
sum[index << 1 | 1] = lazy[index] * rn//右子节点
lazy[index] = 0//更新完子节点后,当前lazy清空
}
}
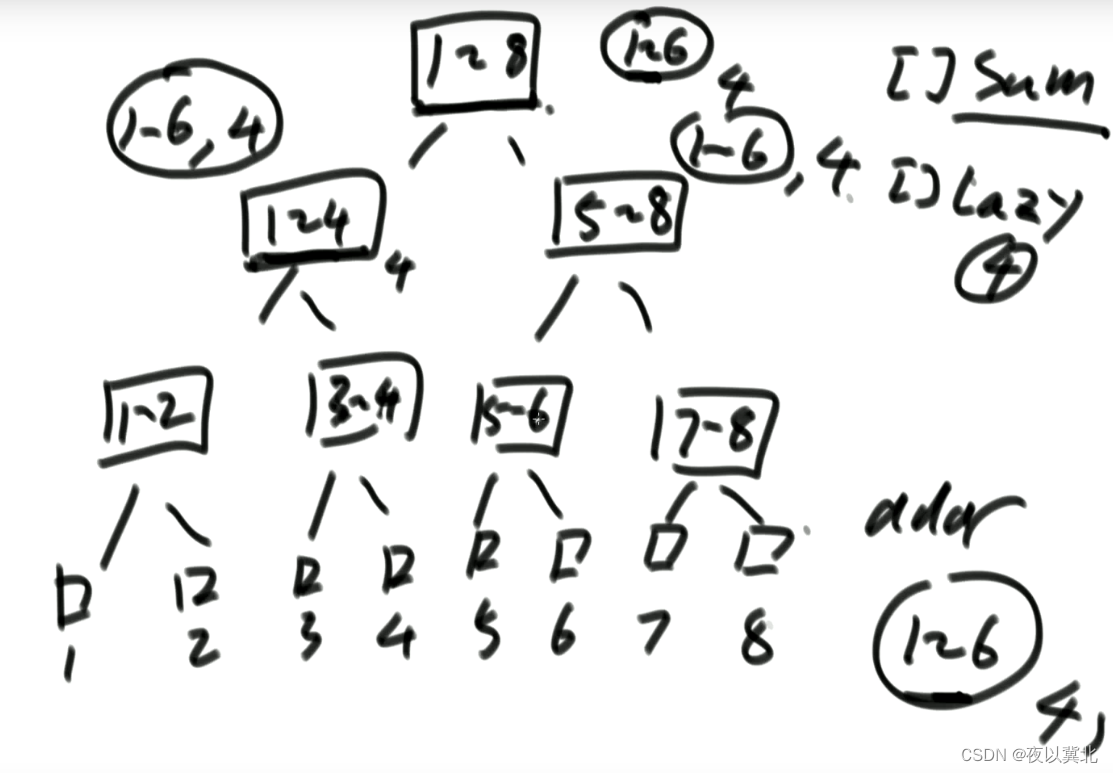
再举个例子演示一下累加方法的运作流程:
首先有一棵根节点为1-4的线段树,lazy数组和sum数组全为0
下发第一个1-2区间所有数加5的任务,这个任务首先会来到根节点,此时任务范围不能全包括当前实际范围,求一下实际位置的中点位置,此时代码的设计就是将之前1-4的懒更新任务下发给两个子节点,而现在是还没有懒更新任务的,所以懒更新代码就跳过了这个条件,将1-2区间所有数加5这个任务下发给线段树的1-4的两个子节点,然后判断子节点是否需要接这个任务;
发现任务范围包括了1-2的实际范围,更新当前1-2的sum,对应lazy数组的1-2位置设置为5,左侧任务执行完毕,发现任务范围的右边界没有到达右子节点的左边界,不需要接任务
最后汇总更新得到1-4的sum;
下发第二个3-4区间所有数加7的任务,来到根节点,发现任务范围不能全包括当前的实际范围,求一下实际位置的中点位置,此时1-4上也没有lazy任务下发,将3-4区间所有数加7这个任务下发给线段树的1-4的两个子节点,然后判断子节点是否需要接这个任务;
此时发现任务范围的左边界没有到达左子节点的右边界,不需要接任务,发现任务范围包括了3-4的实际范围,更新当前3-4的sum,对应lazy数组的3-4位置设置为7,右侧任务执行完毕;
最后汇总更新得到1-4的sum;
下发第三个1-4区间所有数加2的任务,来到根节点,发现任务范围全包当实际范围,更新sum,b并将lazy对应的‘1-4’位置设置为2
下发第四个1-3区间所有数加6的任务,来到根节点,发现任务范围不能全包括当前的实际范围,吃啥1-4的lazy位置又不为0,懒不住了,就得将lazy下发给子节点,进入pushDown,将1-4对应的lazy下放,子节点对应的lazy位置的值都+2,更新sum,然后当前1-4位置的lazy清空,然后剩下流程就是判断线段树的1-4节点的子节点是否接1-3的任务…
最后是update方法的实现
//!!!!!!!!!!这是伪代码!!!!!!!!!!
//L和R表示任务的范围,C表示要修改成的数,l和r表示来到的实际范围,index表示l和r对应的lazy数组.update数组或者sum数组的下标索引
func update(L,R,C,l,r,index int) {
if L < l && r > R {//任务范围大于实际范围
//注意这里的update和change是共同使用的,只有当update对应位置修改成TRUE,change才有效
update[index] = true
change[index] = C
sum[index] = C * (r-l+1)//前面全部东西都不要了
lazy[index] = 0
return
}
//任务范围并没有全包括当前实际范围,懒不住就要把所有懒任务下发
mid = (1+r)>>1
pushDown(index, mid -l +1,r-mid)//汇总
//左孩子是否需要接任务
if(L <= mid) {
add(L,R,C,1,mid,index<<1)
}
//右孩子是否需要接任务
if(R > mid) {
add(L,R,C,mid+1,r,index<<1 | 1)
}
//左右孩子做完任务,更新父范围的sum
pushUp[index]
}
//之前懒增加和懒更新,从父范围到子范围的分发机制函数,ln表示左子树的元素个数,rn表示右子树的元素个数
func pushDown(index,ln,rn) {
if update[index] {//首先检查父范围是否有懒更新、懒增加
update[index << 1] = true//左子节点分到懒更新、懒增加
update[index << 1 | 1] = true//右子节点分到懒更新、懒增加
change[index << 1] = change[index]
change[index << 1 | 1] = change[index]
lazy[index << 1] = 0
lazy[index << 1 | 1] = 0
sum[index << 1] = change[index] * ln
sum[index << 1 | 1] = = change[index] * rn
update[index] = false//父范围任务分发完毕
}
if lazy[index] != 0 {
lazy[index << 1] += lazy[index]//更新lazy[index]的左子节点
sum[index << 1] += lazy[index] * ln//左孩子累加,然后总和累加
lazy[index << 1 | 1] += lazy[index]//更新lazy[index]的右子节点
sum[index << 1 | 1] = lazy[index] * rn//右子节点
lazy[index] = 0//更新完子节点后,当前lazy清空
}
}
举个例子演示前面机制:首先有一棵根节点为1-8的线段树,lazy数组、update数组和sum数组全为0
(这里有个点注意:如果父范围有懒更新,那么后面子范围的懒更新、懒增加其实是无效的,因为父范围的懒更新要比子范围的要晚到)
第一个任务:1-4所有数加2,先来到1-8发现实际范围大,到1-4懒住,更新对应位置的sum为8和lazy为2,5-8不要这个任务,然后汇总更新1-8的sum为8
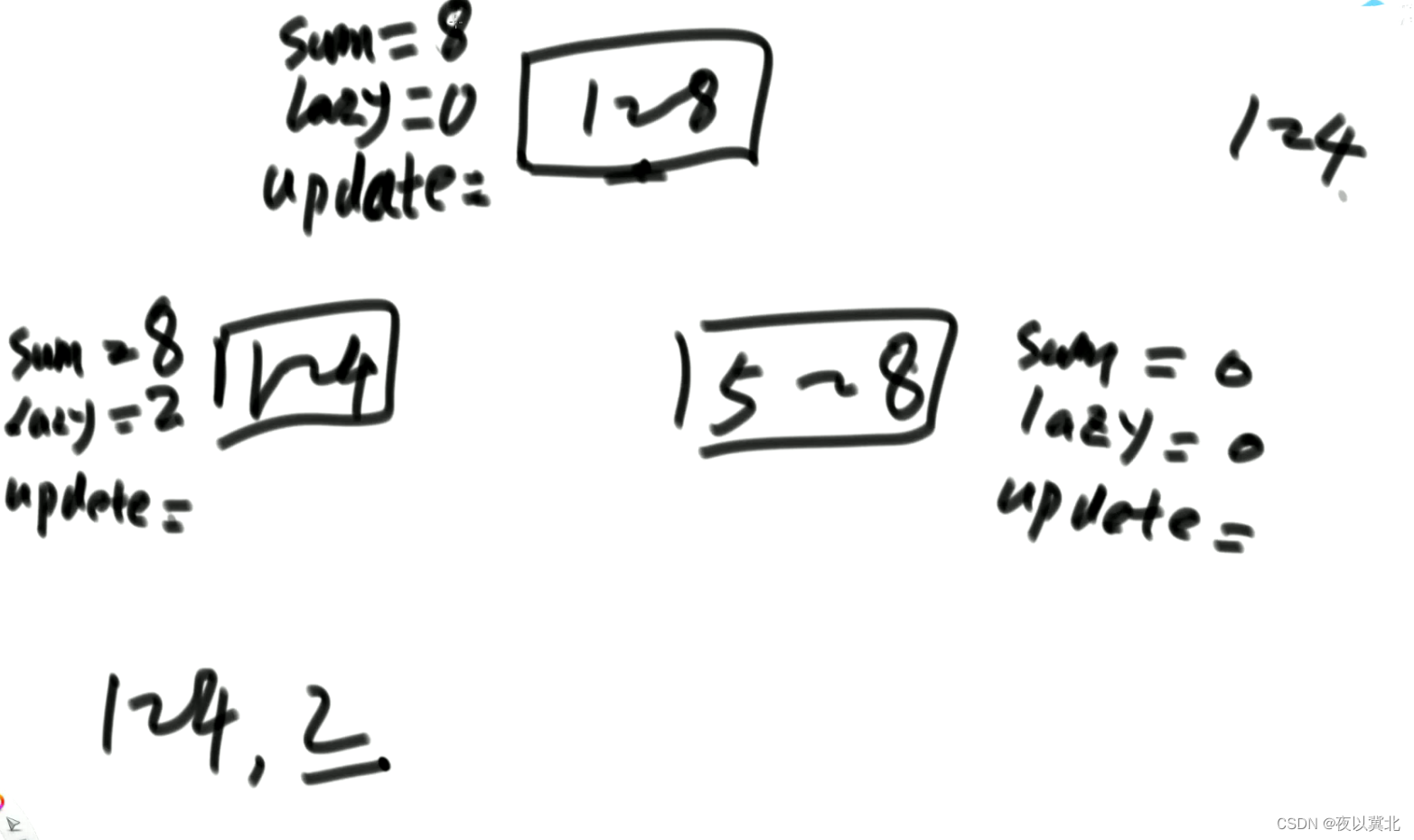
第二个任务:5-8所有数改成1,先来到1-8发现实际范围大,1-4不要这个任务,5-8懒住,更新sum为2*4=8,清空lazy,update改成1,汇总更新1-8的sum为12
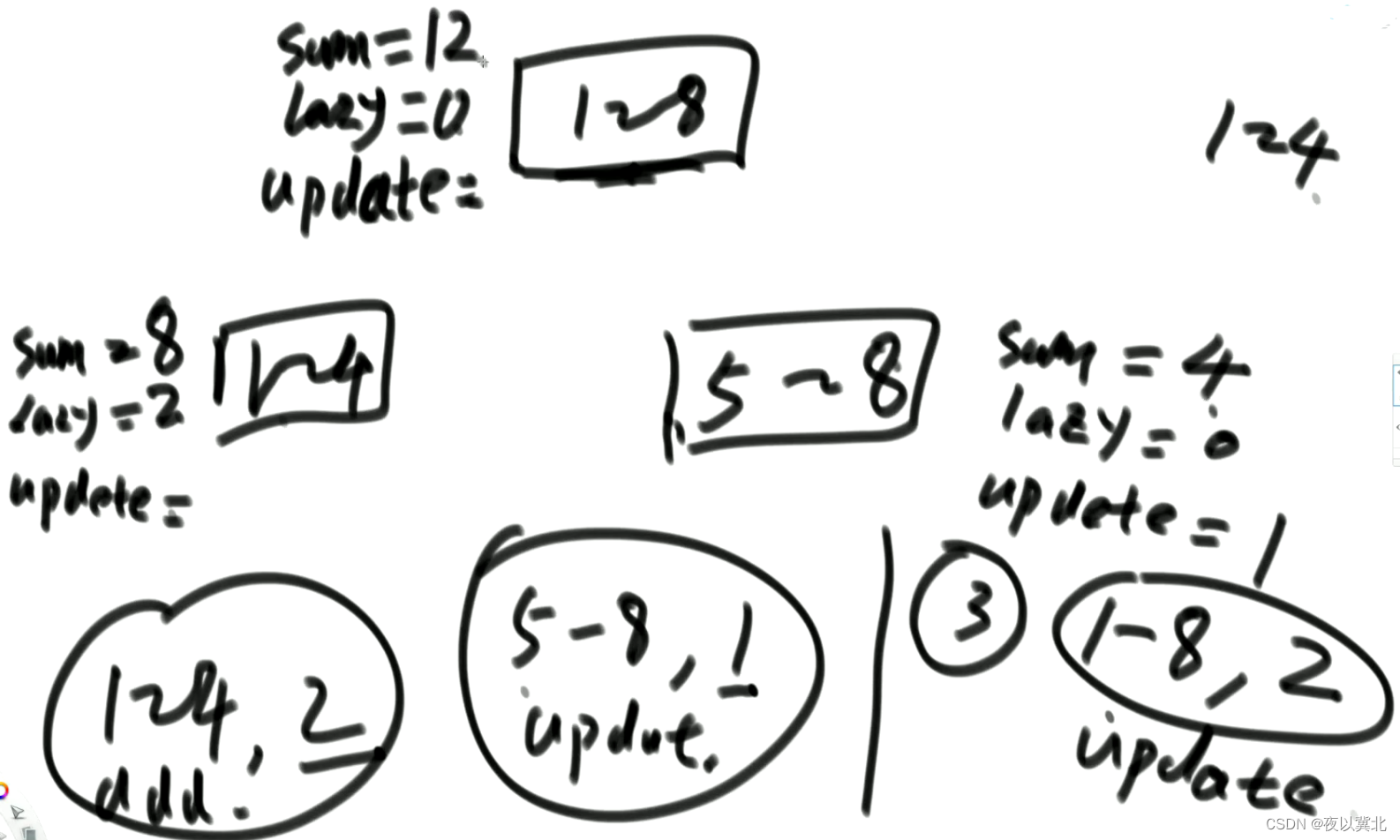
第三个任务:1-8所有数改成2,来到1-8懒住,sum更新为16,lazy清空,update为2
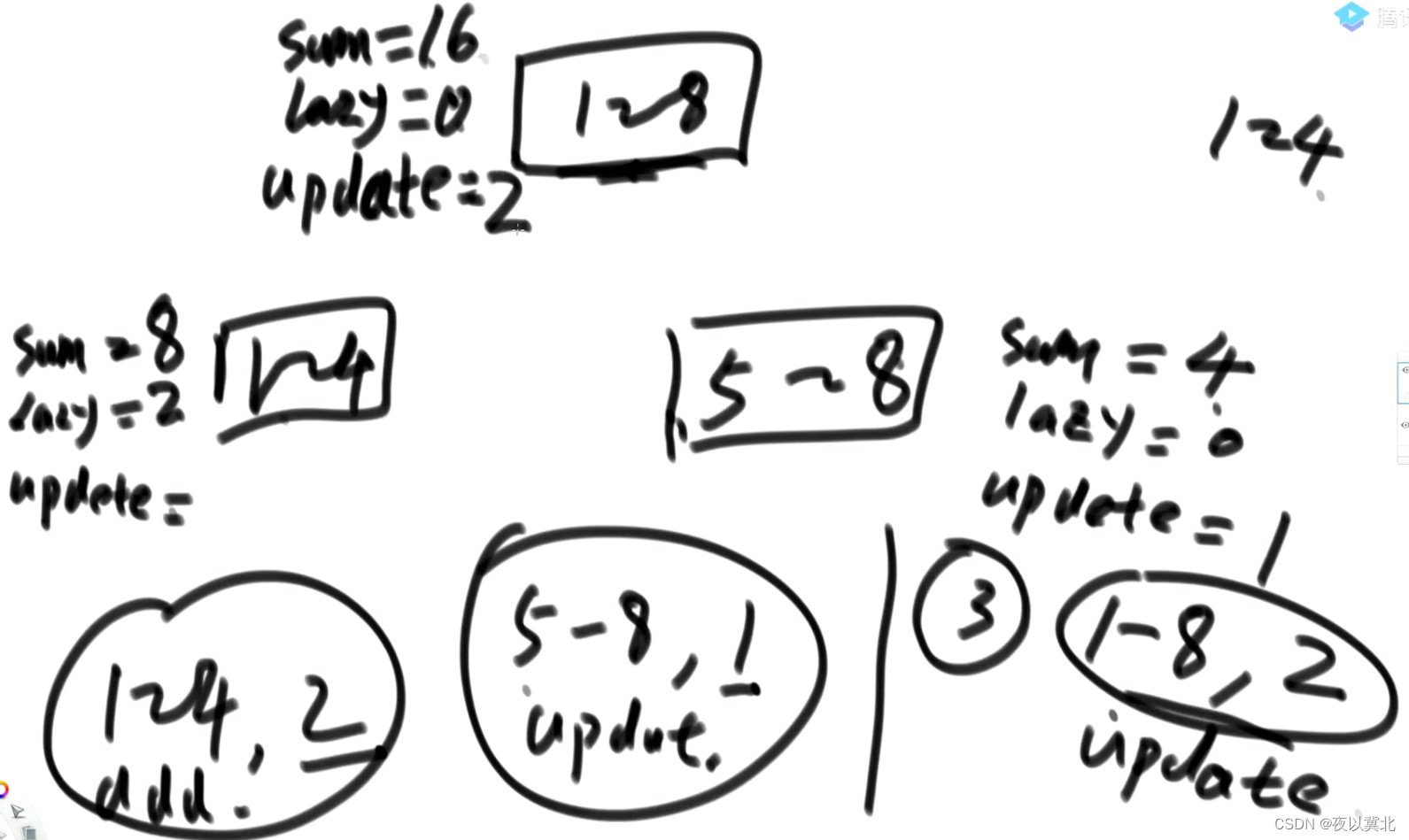
第四个任务:1-8所有数加3,来到1-8懒住,sum改为40,lazy改为3
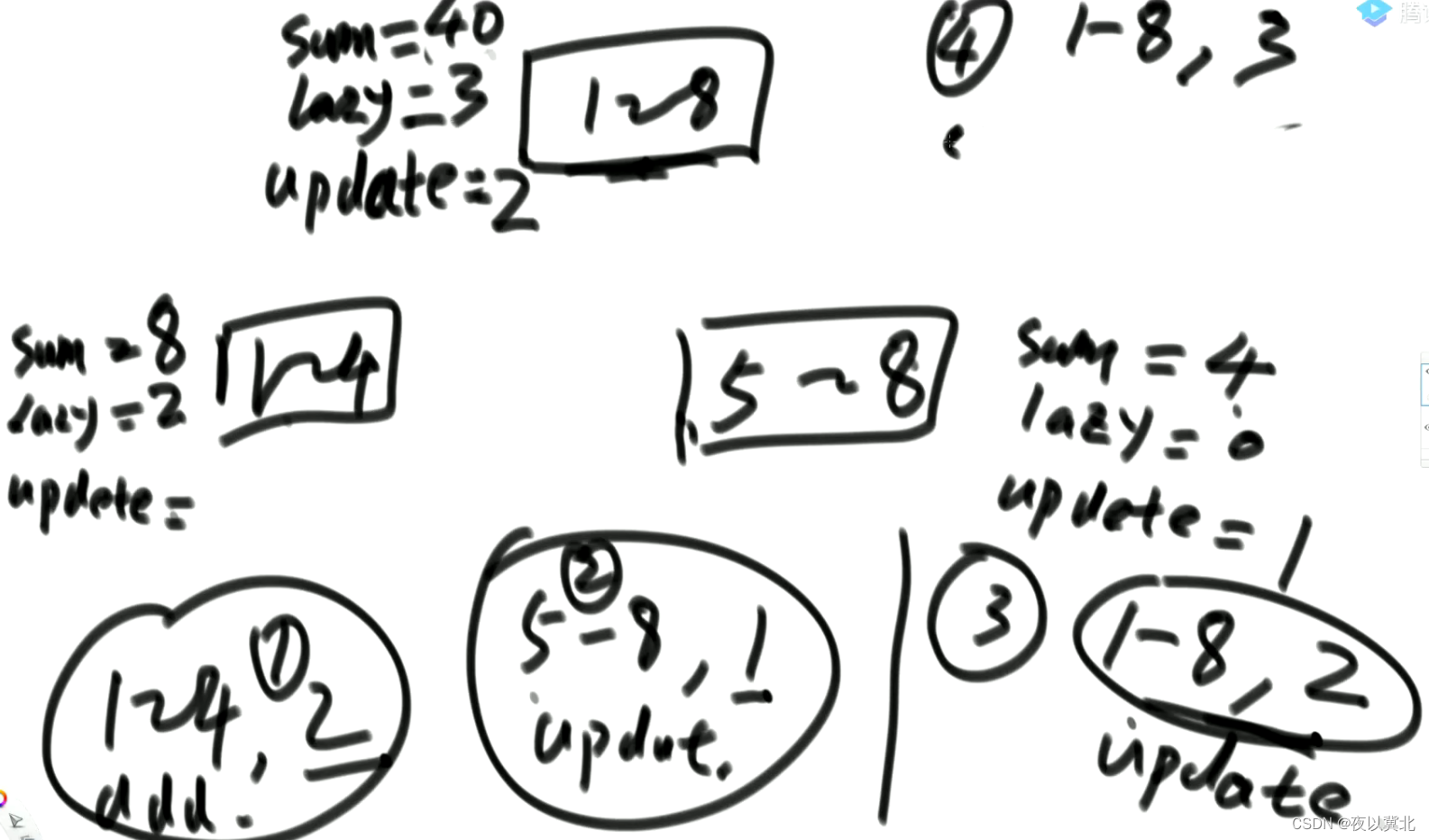
第五个任务:1-8范围加5,lazy改成8,sum改为80

第六个任务:1-7范围加1,来到1-8发现懒不住,在1-7执行之前先将1-8全部任务下发,先发1-8的update任务,发现update有值,则下发到子节点时,两个子节点全部任务清空,sum改成8,lazy改为0,update改成2,然后再将1-8的lazy任务下发,最后再将1-7加1的任务下发…
最后是query函数(查询一个范围的sum),机制实现:
func query(L,R,C,l,index int) {
if L < l && r > R {//任务范围大于实际范围
return sum[index]
}
//任务范围并没有全包括当前实际范围,要把任务下发
mid = (1+r)>>1
pushDown(index, mid -l +1,r-mid)
ans := 0
if(L <= mid) {
ans += query(L,R,1,mid,index<<1)
}
if(R > mid) {
ans += query(L,R,mid+1,r,index<<1 | 1)
}
return ans
}
manacher算法
在O(N)时间复杂度下求字符串所有回文子串的算法,也是求最大回文子串最高效的算法。
1.回文串长度的计算
如果一个字符串是回文串,那么该字符串必是中心对称的。故我们可以选择一个中心,从它开始,向两边逐一判断字符是否相同,拓展回文串长度。由于回文串可以是奇回文串也可以是偶回文串,我们需要选择一个字符或者选择两个字符中间作为中心进行逐一判断,故一共有 N + N - 1个中心。
2.回文串处理和相关参数补充
回文串有aba和abba的形式,因此在每两个字符间及字符串头、尾加上一个字符(什么字符都可以);
回文半径数组,在从左往右遍历的过程中记录每一个数据对应的回文半径
回文串的最大右边界的标号数字R 以及这个回文串的中心点标号数字C
接上来说明一下上面这两个参数的不同情况:
(1)中心点在最大右边界之外时,例如 #1#0#1#0#1# 刚开始遍历时,最大右边界的标号是-1,而中心点(现在是第一个字符)的标号是0,这种情况直接将右边界扩展第一个遍历到的字符的最大右边界位置;
(2)中心点在最大右边界的内部
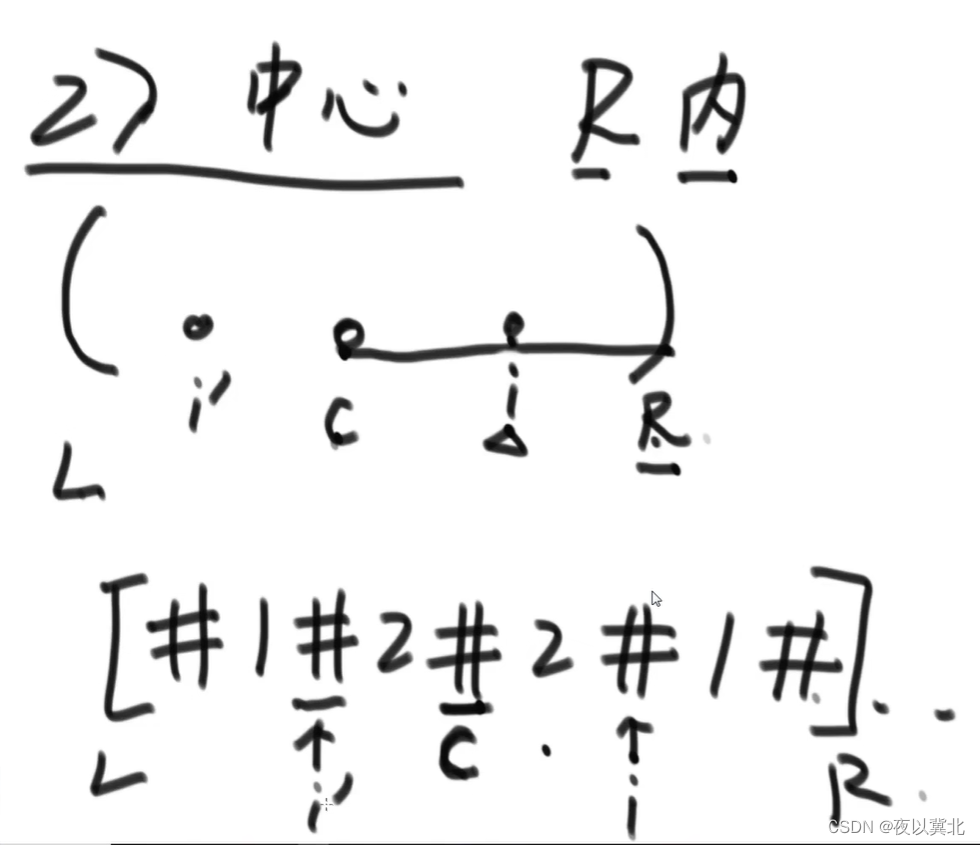
而根据i’的位置再细分成两种情况,第一种情况是i’的回文串在目前最大回文串的范围内,比如下面这样的(注意每个字符之间还是有一个特殊字符,这里没写而已),这种情况就是人为根据i的对称点i’的回文区域状况,能不能不扩充也能获得i的回文区域状况
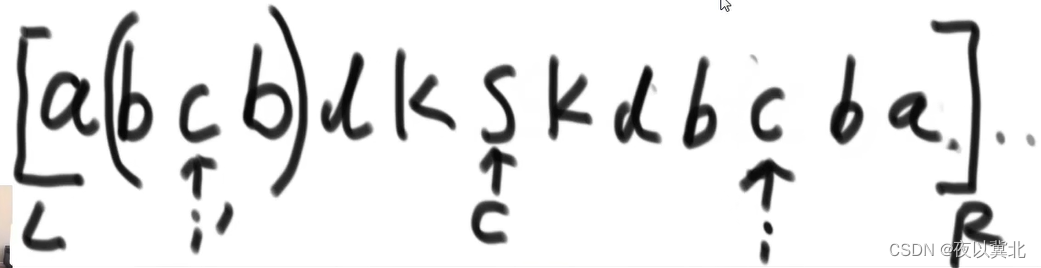
第二种情况是i’的回文串在目前最大回文串的范围内外都有涉及,比如下面这样的(注意每个字符之间还是有一个特殊字符,这里没写而已)
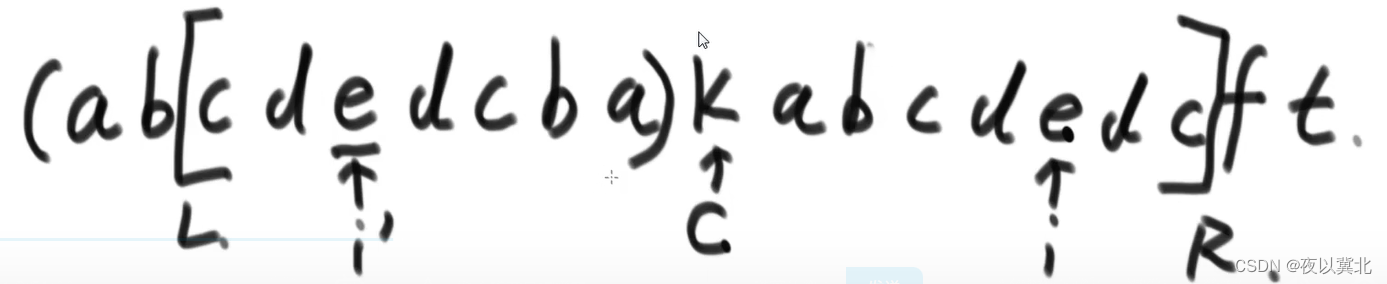
第三种情况是i’的回文串刚好压线到目前最大回文串的边界,比如下面这样的(注意每个字符之间还是有一个特殊字符,这里没写而已)
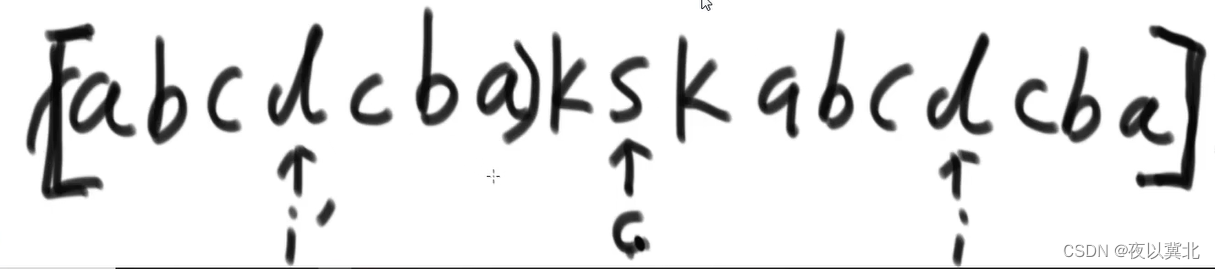
单调栈:每个元素最多各自进出栈一次,复杂度是O(n)
单调递增栈:①在一个队列中针对每一个元素从它右边寻找第一个比它小的元素;②在一个队列中针对每一个元素从它左边寻找第一个比它小的元素
单调递减栈:①在一个队列中针对每一个元素从它右边寻找第一个比它大的元素;②在一个队列中针对每一个元素从它左边寻找第一个比它大的元素
具体的操作流程(例如单调递减栈,注意压入栈的是数据对应的下标,不是数据本身):
从左往右遍历一个队列 3 7 5 2 6 1,
第一个元素3压入栈,【3】
第二个元素7大于3,元素3弹出,7压栈,【7】
第三个元素5小于7,5压栈,【7 5】
第四个元素2压栈,【7 5 2】
第五个元素6大于2,2弹出,6大于5,5弹出,6压栈,【7 6】
第六个元素1小于6,1压栈,【7 6 1】
之后逐个元素。
| 弹出元素X(下标->元素) | 右边比X大的(入栈的当前元素) | 左边比X大的(弹出元素的底下一个元素) |
|---|---|---|
| 0->3 | 1->6 | 无 |
| 3->2 | 4->6 | 2->5 |
| 2->5 | 4->6 | 1->7 |
| 5->1 | 无 | 4->6 |
| 4->6 | 无 | 1->7 |
| 1->7 | 无 | 无 |
Morris遍历
当前节点记为cur,一开始cur来到整棵树的根节点,根据以下不同情况进行移动(直到cur指向null):
1)cur无左树,cur = cur.right
2)cur有左树,找到cur的左子树部分最右的节点(如果左边都是左子树,那么cur的左子节点就是最右的节点),记为mostright
(1)mostright的右指针指向null的,mostright.right = cur,cur = cur.left
(1)mostright的右指针指向cur的,mostright.right = null,cur = cur.right
//这是伪代码,随便写的,逻辑意思在就行
func reverseEdge(head Node) Node {
Node pre = head
Node ss = head.right
Node ssnext = null
for ss != null {
ssnext = ss.right
ss.right = pre
pre= ss
ss = ssnext
}
return pre
}
func printEdge(Node head) {
Node tail = reverseEdge(head)
Node cur = tail
for cur != null {
fmt.println(cur.value)
cur = cur.right
}
reverseEdge(tail)
}
func morris(head Node) {
if head == null {
return
}
Node cur = head
Node mostRight = null
while cur != null {
//先判断cur有没有左树
mostRight = cur.left//cur先别动,先将cur的左节点给到mostRight,如果cur没有左子树,那么mostRight为空
if mostRight != null {//有左树的情况
//而mostRight已经来到了左子树的部分,接下来要找到当前子树的最右节点
for mostRight.right != null && mostRight.right !== cur {
mostRight = mostRight.right
}
//从while出来后一定是最右节点了
if mostRight.right == null {//这种情况是第一次来到最右节点,将其右子节点指向cur,cur左移
mostRight.right = cur
/*
先序遍历:代码补充地方一 (能回到自己两次的节点在第一次要打印)
fmt.println(cur.value)
*/
cur = cur.left
continue
} else {//这种情况是第二次来到最右节点,将其右子节点由指向cur重新指向null,然后cur右移
mostRight.right = null
/*后序遍历代码补充地方一
printEdge(cur.left)
*/
}
}
/*
先序遍历:代码补充地方二 (没有左树的节点要直接打印)
else {fmt.println(cur.value)}
*/
/*
中序遍历:代码补充地方 (在cur右移前打印)
fmt.println(cur.value)
*/
//若没有执行上述的程序,表示cur无左子树,cur右移即可
cur = cur.right
}
/*后序遍历代码补充地方二
printEdge(cur.left)
*/
}
由Morris序改先序、中序和后序都可以:
先序:对于Morris序中只能遍历一次的数据直接打印,能遍历两次的第一次就打印
中序:对于Morris序中只能遍历一次的数据直接打印,能遍历两次的第二次才打印(总结为只要一个节点要往右移动就打印)
后序:对于Morris序中能遍历两次的数据,第二次遇到时将其左子树的全部右边界逆序打印(这里的逆序打印用链表翻转)
利用Morris序可以以低空间复杂度完成很多题目:
例一:判断一棵树是否是二叉搜索树(儿叉搜索树就是左边都比根小,右边都比根大,中序遍历就是一个递增的数列),就可以在Morris序改中序遍历的地方设置pre记录上一个遍历的值和cur记录当前遍历的值,如果pre > cur就不符合了;
例二:求一棵树的最小高度?要实现两个机制:能得知当前节点的高度以及能判断当前节点是叶节点
得知当前节点的高度的机制实现:
首先cur来到根节点a,高度就是1,当cur无左树,cur右移,此时高度++
在Morris遍历程序中,cur指向a,a有左子树且完成e指向a,cur移动到左子节点b,此时当前节点b遍历的上一个节点a的左子节点就是当前节点**(pre.left == cur)**,那么当前节点b的高度就是上一个遍历节点a的高度++(例如来到b),之后cur来到d后,d没有左子节点,cur通过右树回到b,而此时遍历的上一个节点是d,不满足(pre.left == cur),然后就去数一下b左树上的右边界有几个点,减掉就是当前节点b高度,然后来到e,看e有没有左子树的最右节点指向e,有就减左树上的右边界有几个点得到高度,没有就高度++,来到a…
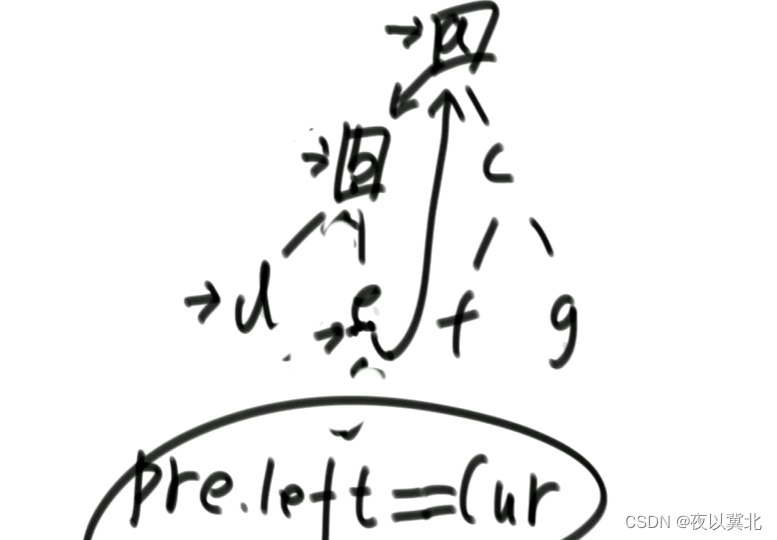
判断当前节点是叶节点的机制实现:
所有叶节点都会在遍历两次后回到上一个节点时被重新发现一次,因为上一个节点的高度是要通过左子树部分的右边界节点更新的(注:整棵树最右的节点是没有人发现的)
比如下面这棵树,经过操作3->1,12->3,11->10,然后11回到10的时候,恢复11->null,检查11是否是叶节点,如果是就算出11的高度,更新min,然后往右走来到12,12回到3,恢复12->null,然后到3时,重新检查12是否是叶节点,如果是就算出12的高度,更新min,然后回到1,恢复3->null,检查3是否是叶节点,不是就不参与更新min,来到4直接走,来到5,经过操作9->5,8->6,通过8回到6,重新检查8是否是叶节点,如果是就算出8的高度,更新min,6去到9,9回到5,恢复9->null,重新检查9是否是叶节点,如果是就算出9的高度,更新min,去到7,右走结束
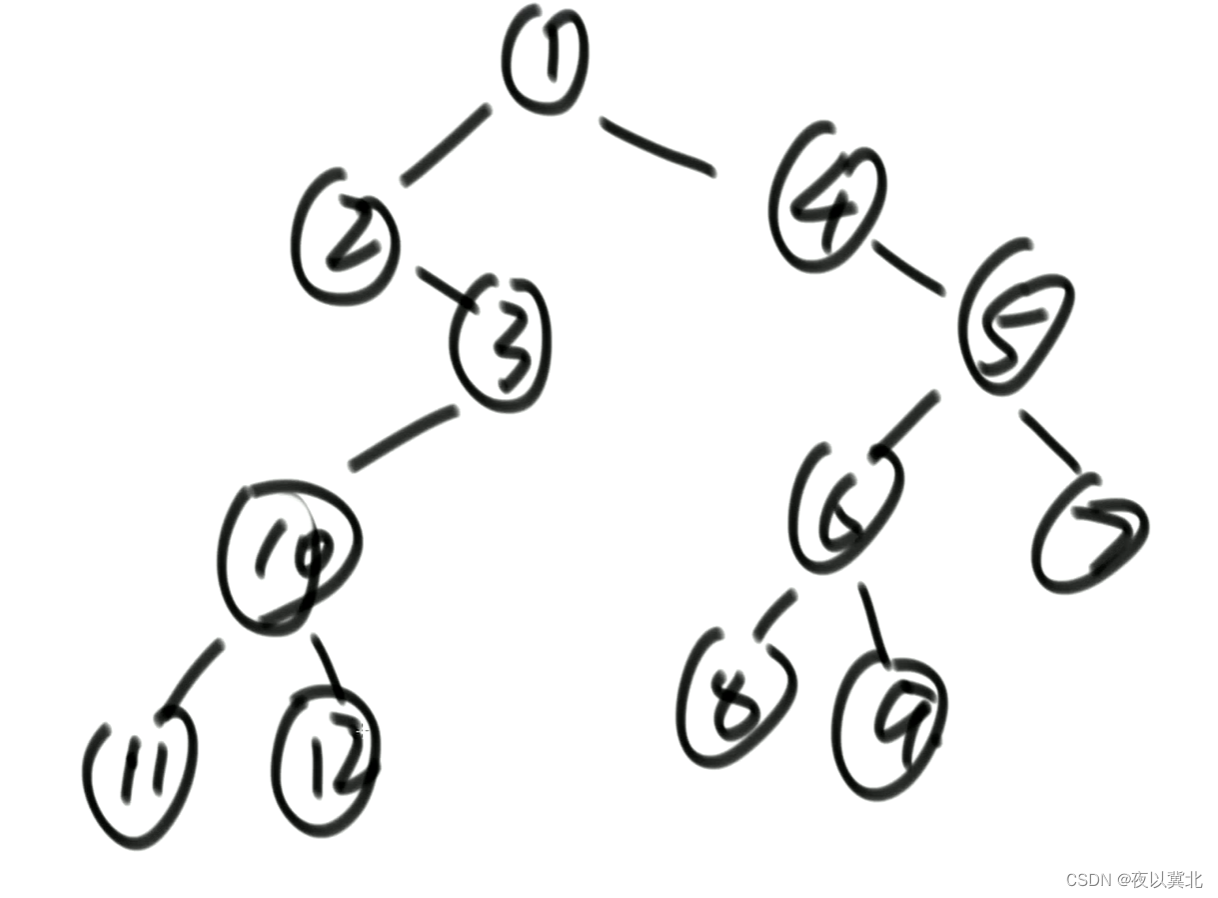
//这是伪代码,随便写的,逻辑意思在就行
func morrisMin(head Node) int {
if head == null {
return 0
}
Node cur = head
Node mostRight = null
int curLevel = 0
int minHeight = 参数最大数字
while cur != null {
mostRight = cur.left
if mostRight != null {
int leftHeight = 1
for mostRight.right != null && mostRight.right !== cur {
leftHeight++
mostRight = mostRight.right
}
if mostRight.right == null { //第一次到达
curLevel++
mostRight.right = cur
cur = cur.left
continue
} else { //第二次到达
if mostRight.left == null { //判断出是否为叶节点
minHeight = min(minHeight, curLevel)
}
curLevel -= leftHeight
mostRight.right = null
}
} else { //只能一次到达
curLevel++
}
cur = cur.right
}
//后面就是管一下整棵树最右节点
int finalRight = 1
cur = head
for cur.right != null {
finalRight++
cur = cur.right
}
if cur.left == null && cur.right == null {
minHeight = min(minHeight, finalHeight)
}
return minHeight
}
Morris遍历总结:
当算法求解过程中,遇到这样流程:来到一个节点X,需要左子树和右子树都给信息并且整合,这就不能用Morris遍历,老老实实二叉树的递归套路;如果遇到这样流程:用完左树信息后就不再需要了,信息可以传递就可以用Morris遍历






















 2207
2207











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










