二分法查找

LeetCode704 二分查找

一直以来，都以为二分法很简单，但昨天一写代码就出问题，感觉还是理解得不够透彻。

二分查找

难度:简单

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

提示：

1. 你可以假设 nums 中的所有元素是不重复的。
2. n 将在 [1, 10000]之间。
3. nums 的每个元素都将在 [-9999, 9999]之间。

二分法可以有两种写法，定义区间不同，写法不同。值得注意的是，此区间在循环过程中保持不变，即mid改变，但区间性质不变。

1. target位于左闭右闭 []区间内

   此时，low==high可以成立
   

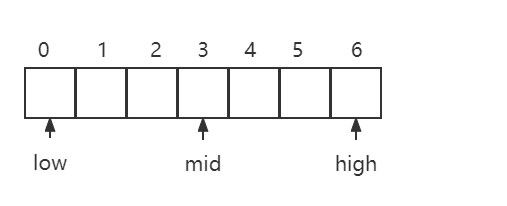
   假设target 为2，则下一步，high = mid - 1（保持闭区间，且无需再次查找mid处）
   

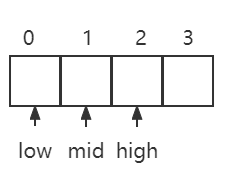
   同理，low = mid + 1

   故用Java实现

   class Solution {
       public int search(int[] nums, int target) {
            int low = 0, high = nums.length - 1;
            while (low <= high){
                int mid = low + (high-low)/2;
                if( nums[mid] == target){
                    return mid;
                }
                else if( nums[mid] > target){
                    high = mid - 1;
                }
                else if (nums[mid] < target){
                    low = mid + 1;
                }
            }
            return -1;
       }
   

2. target位于左闭右开 []区间内

   此时，low==high无意义，因为high本身并不在区间内。
   

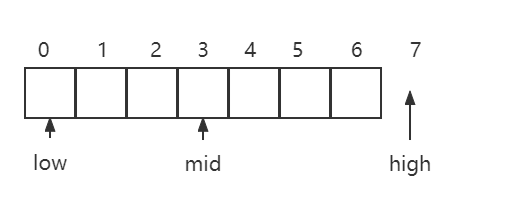
   假设target 为2，则下一步，high = mid （保持左闭右开区间，且无需再次查找mid处）
   

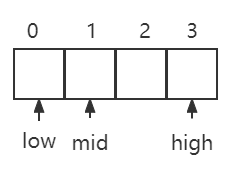
   但由于左侧为闭区间，则low = mid + 1

   故用Java实现

   class Solution {
       public int search(int[] nums, int target) {
            int low = 0, high = nums.length;
            while (low < high){
                int mid = low + (high-low)/2;
                if( nums[mid] == target){
                    return mid;
                }
                else if( nums[mid] > target){
                    high = mid;
                }
                else if (nums[mid] < target){
                    low = mid + 1;
                }
            }
            return -1;
       }
   }
   

LeetCode 35 搜索插入位置

35. 搜索插入位置
难度：简单
给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。如果目标值不存在于数组中，返回它将会被按顺序插入的位置。nums为无重复元素的升序排列数组
请必须使用时间复杂度为 O(log n) 的算法。

插入位置分四种情况。target在所有元素之前，target恰在数组中，target在数组元素之间，target在所有元素之后。

1. 暴力解法

class Solution {
    public int searchInsert(int[] nums, int target) {
        for (int i = 0;i < nums.length;i++){
            if(nums[i] >= target){
                return i;  //因数组升序，故一旦大于target，便可插入当前位置。
            }
        }
        return nums.length;
    }
}

2. 二分查找

class Solution {
    public int searchInsert(int[] nums, int target) {
        int low = 0, high = nums.length - 1;
        while(low <= high){
            int mid = low + ((high-low)>>1); //此处若采取移位运算，必须带括号
            if(target == nums[mid]){
                return mid;
            }
            else if(target > nums[mid]){
                low = mid + 1;
            }
            else if(target < nums[mid]){
                high = mid - 1;
            }
        }
        return high + 1; //计算可知，其余三种情况皆可由high+1解出
    }
}

LeetCode 278 第一个错误的版本

278.第一个错误的版本
错误的版本之后的所有版本都是错的。假设你有 n 个版本 [1, 2, …, n]，你想找出导致之后所有版本出错的第一个错误的版本。你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。

/* The isBadVersion API is defined in the parent class VersionControl.
      boolean isBadVersion(int version); */

public class Solution extends VersionControl {
    public int firstBadVersion(int n) {
        int low = 1, high = n;
        while(low < high){
            int mid = low + ((high-low)>>1);
            if(!isBadVersion(mid)){
                low = mid + 1;
            }
            else if(isBadVersion(mid)){
                high = mid;
            }
        }
        return low;
    }
}

LeetCode 69 Sqrt(x)

69.Sqrt(x)
给你一个非负整数 x ，计算并返回 x 的 算术平方根 。
由于返回类型是整数，结果只保留 整数部分 ，小数部分将被 舍去 。注意：不允许使用任何内置指数函数和算符，例如 pow(x, 0.5) 或者 x ** 0.5 。

class Solution {
    public int mySqrt(int x) {
        int low = 0, high = x;
        int res = -1;
        while(low <= high){
            int mid = low + (high-low)/2;
            if((long)mid * mid <= x){
                res = mid;
                low = mid + 1;
            }else{
                high = mid - 1;
            }
        }
        return res;
    }
}