李宏毅机器学习 hw11 boss baseline分享

hw11

代码

任务描述

给定真实的图片（有label）和手绘图片（无label），使用领域适应技术来预测绘画图片的类别。
我们采用的模型结构如下：

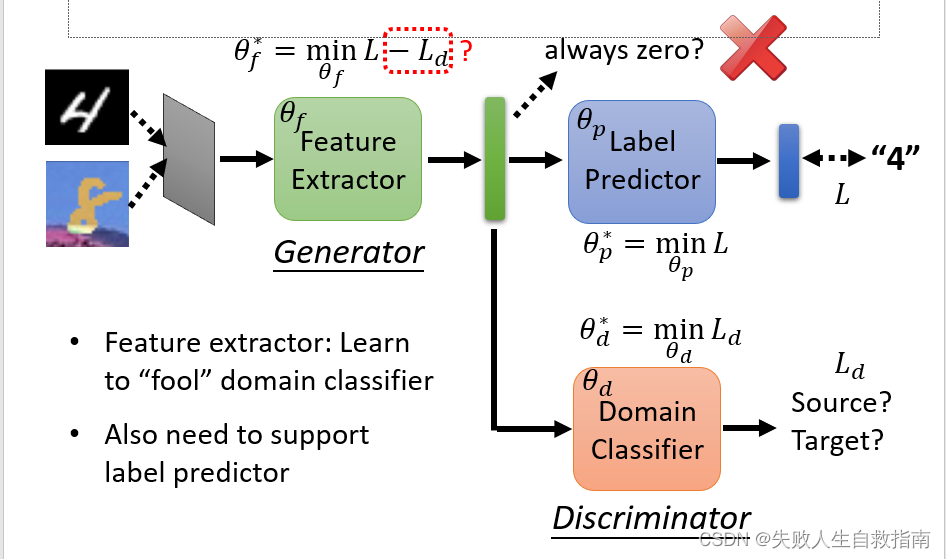
模型由三部分组成，首先是特征提取器（Feature Extractor）负责提取出两个领域的图片所具有的共同特征，标签预测器（Label Predictor）负责对提取出的共同特征进行正确的分类，最后是领域分类器（Domain Classifier）负责判断提取的特征是属于哪一个领域的，与特征提取器进行对抗训练。
代码的大致框架助教已经帮我们写好了，我们要做的就是在已有结构上进行调整，提高正确率，同时，助教还给我们提供了训练的曲线，如图

从这个曲线我们可以得到两点信息：

1. 当训练正确率已经过拟合时，你也不要停止训练，因为从图中可以看到此时测试集的正确率其实还在提高。
2. 领域分类器的正确率整体上一直在下降，最后下降到0.5左右才算是一个好的结果，这说明它就是完全随机分的，根本不能成功区分特征了，说明特征提取器已经达到了很好的效果。

实验要求

Strong baseline

1. 增大epochs 200->3000
2. 根据DANN的论文动态调整$\lambda$
   $$\lambda =\frac{2}{e^{-10epoch/epochs}+1}-1$$
   画出来的曲线如图：
   
   标签预测器和特征提取器是放在一起训练的，其中标签预测器的loss为loss1,领域分类器的loss为loss2,
   总的$$loss=loss1-\lambda loss2$$
   $\lambda$刚开始时很小，模型主要训练标签预测器使souce domain提取的特征能够被很好预测，后面$\lambda$逐渐增大，强调领域分类器的loss，即特征提取器要能够骗过领域分类器，将target domain的特征拉到与souce domain一样的空间，从而保证正确率。
   提交结果如下:
   
   已经过了boss baseline,但是只过了一点，还能再提高！

Boss baseline

使用strong baseline得到的模型对target图片生成伪标签（pseudo-label）。为保证伪标签的可靠性，所产生的伪标签概率高于0.95才会被使用，然后用生成的伪标签来训练student net(初始时student net 和 teacher net都是strong baseline得到的模型),而teacher net 的更新较慢每一个epoch更新一次，teacher net网络权重中0.9的权重来自于自己，0.1的权重来自于更新后的student net。
训练400个epoch。提交得到的结果如下：

提高了1.5个百分点左右，生成伪标签的技巧是打榜冲刺阶段很常用的技巧，可以了解一下！