长短时记忆网络（LSTM）深度解析-CSDN博客

本文链接：https://blog.csdn.net/qq_43664407/article/details/148028135

1. 模型结构详解

1.1 核心组件

LSTM通过门控机制和细胞状态解决RNN的长期依赖问题，其单元结构如下:

输入 → 遗忘门 → 输入门 → 细胞状态更新 → 输出门 → 输出

1.1.1 核心门控结构

遗忘门（Forget Gate）：决定丢弃多少历史信息
输入门（Input Gate）：决定存储多少新信息
输出门（Output Gate）：决定当前隐藏状态的输出

1.1.2 细胞状态（Cell State）

作用：跨时间步传递长期记忆
更新规则：通过遗忘门和输入门动态调整

1.1.3 输入输出维度

输入：当前时间步输入 xt∈Rd 和前一隐藏状态 ht−1∈Rh
输出：当前隐藏状态 ht∈Rh 和细胞状态 Ct∈Rh

2. 数学原理与推导

2.1 前向传播公式

2.1.1 门控计算

遗忘门：
$f_t = \sigma(W_f \cdot [h_{t-1}, x_t] + b_f)$
输入门：
$i_t = \sigma(W_i \cdot [h_{t-1}, x_t] + b_i)$
候选细胞状态：
$\tilde{C}t = \tanh(W_C \cdot [h{t-1}, x_t] + b_C)$

2.1.2 细胞状态更新

$C_t = f_t \odot C_{t-1} + i_t \odot \tilde{C}_t$

2.1.3 输出门与隐藏状态

输出门：
$o_t = \sigma(W_o \cdot [h_{t-1}, x_t] + b_o)$
隐藏状态：
$h_t = o_t \odot \tanh(C_t)$

2.2 反向传播（梯度流动分析）

细胞状态梯度：
$\frac{\partial \mathcal{L}}{\partial C_t} = \frac{\partial \mathcal{L}}{\partial h_t} \odot o_t \odot (1 - \tanh^2(C_t)) + \frac{\partial \mathcal{L}}{\partial C_{t+1}} \odot f_{t+1}$
参数更新：梯度通过时间步累加，但细胞状态提供低衰减路径

3. 代表性变体及改进

3.1 Peephole LSTM

改进点：门控信号引入细胞状态信息
公式修正：
$f_t = \sigma(W_f \cdot [C_{t-1}, h_{t-1}, x_t] + b_f)$

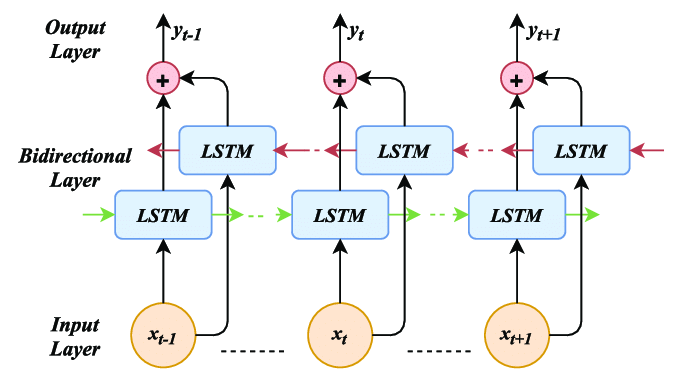
3.2 双向LSTM（Bi-LSTM）

结构：前向LSTM + 后向LSTM → 拼接输出
应用：上下文依赖建模（如命名实体识别）

3.3 深度LSTM

结构：堆叠多层LSTM单元
公式修正：第l层输入为第l−1层的隐藏状态 ht(l−1)

3.4 GRU（门控循环单元）

简化设计：合并输入门与遗忘门 → 更新门
公式对比：
$z_t = \sigma(W_z \cdot [h_{t-1}, x_t])$
$r_t = \sigma(W_r \cdot [h_{t-1}, x_t])$
$h_t = (1 - z_t) \odot h_{t-1} + z_t \odot \tilde{h}_t$

4. 应用场景与优缺点

4.1 应用场景

自然语言处理：文本生成、机器翻译
时间序列预测：股票价格、气象数据建模
语音识别：音频序列到文本的转换

4.2 优缺点对比

优点	缺点
解决长期依赖问题	计算复杂度高（参数量为RNN的4倍）
灵活控制信息流	难以并行化计算
广泛实验验证有效性	超参数调节复杂（如初始状态、梯度裁剪阈值）

5. PyTorch代码示例

import torch
import torch.nn as nn

class LSTMModel(nn.Module):
    def __init__(self, input_size, hidden_size, num_layers=1):
        super().__init__()
        self.lstm = nn.LSTM(
            input_size=input_size,
            hidden_size=hidden_size,
            num_layers=num_layers,
            batch_first=True
        )
        self.fc = nn.Linear(hidden_size, 1)  # 回归任务输出维度为1
    
    def forward(self, x):
        # x形状: [batch_size, seq_len, input_size]
        out, (h_n, c_n) = self.lstm(x)
        # 取最后一个时间步输出
        out = self.fc(out[:, -1, :])
        return out

# 示例：时间序列预测
model = LSTMModel(input_size=3, hidden_size=64, num_layers=2)
criterion = nn.MSELoss()
optimizer = torch.optim.Adam(model.parameters(), lr=0.001)

# 输入数据（假设batch_size=16，序列长度=10，特征维度=3）
inputs = torch.randn(16, 10, 3)
targets = torch.randn(16, 1)  # 回归目标

# 训练步骤
outputs = model(inputs)
loss = criterion(outputs, targets)
optimizer.zero_grad()
loss.backward()
optimizer.step()