1. 数据生成
通过下式产生数据,作为训练集
y=4x4+3x3+2x2+x+1+rand
y=4x^4+3x^3+2x^2+x+1+rand
y=4x4+3x3+2x2+x+1+rand
加入0~1之间的随机数使数据更加接近实际数据
2. 假设
2.1 一个参数
在我们不知道函数类型的情况,先假设一个函数用于拟合上述数据,先假设如下,后续逐步提高阶次。
h(x)=1+θ1x
h(x)=1+\theta_1x
h(x)=1+θ1x
这里的θ1\theta_1θ1,是我们不确定的,那如何确定呢。先想想,如果不使用算法,你如何确定这两个参数,比较直接的做法是不是先假定这个值,如θ1\theta_1θ1=3,先看看效果
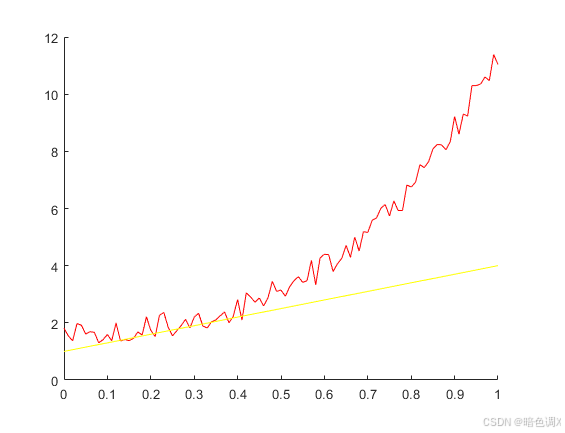
效果似乎不太理想,θ1\theta_1θ1似乎需要再加大一些,θ1\theta_1θ1=4,5,8
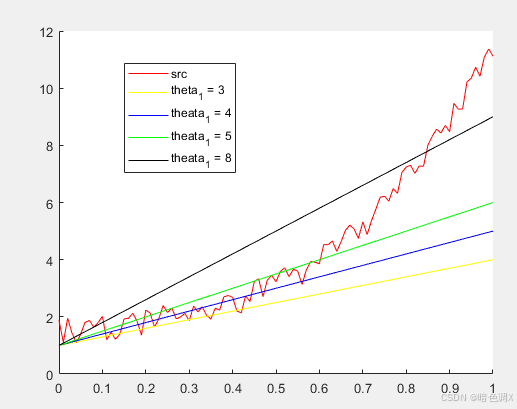
可以看到8的时候似乎比较接近了。但你是如何得出8比较接近的呢。是不是感觉此时黑线的上下是不是数据的差值是不是比较均匀,及黑线之上的数据与黑线之下的数据的差值差不多。用数学的可量化的语言的描述就是此时方差最小。即∑i=1m(h(x(i))−y(i))2\sum^{m}_{i=1}(h(x^{(i)}) - y^{(i)})^2∑i=1m(h(x(i))−y(i))2此时最小,m为样本数据个数。计算θ1\theta_1θ1为不同值时的方差分别为759.6125,505.9800,320.0147,168.1391。θ1\theta_1θ1=8时在视觉上是最匹配的,同时方差也是最小的。但是有没有更好的方法呢,总不能每次数据拟合都不断的人工尝试吧。
这时候聪明的你肯定会想到,让机器枚举遍历阿,每一次数据拟合都不断的尝试,计算最小方差,比如θ1\theta_1θ1从0一直到10,每次步进0.1,最终选择方差最小的那个
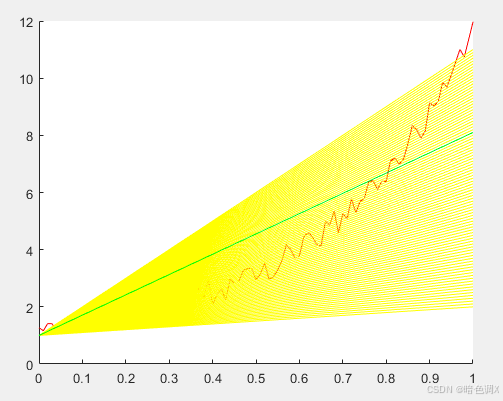
黄线是其他值。绿色线的θ1\theta_1θ1=7.1,方差为155.41。意味只要提高搜索精度,似乎就能快速得到θ1\theta_1θ1的最优值。
其实求拟合的更好就是在求方差的最小值,下图可以看出搜索过程中方差的变化。同时在当前样本中,方差的值只与θ1\theta_1θ1相关。
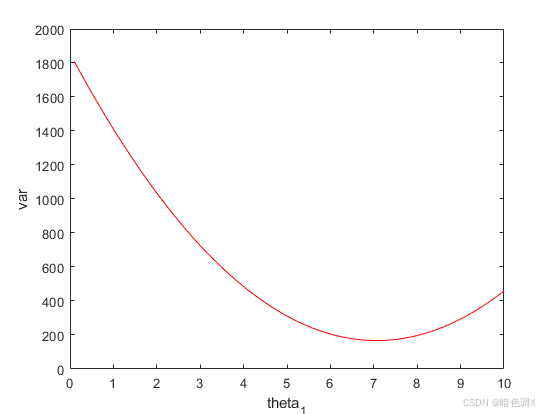
既然拟合是在求θ1\theta_1θ1为何值时方差最小,那么对于只有一个变量θ1\theta_1θ1的假设函数h(x)与原始数据的方差,求其最小值可以用高中的导数求出。
令方差为
J(θ1)=12m∑i=1m(h(x(i))−y(i))2
J(\theta_1) = \frac {1}{2m}\sum^{m}_{i=1}(h(x^{(i)}) - y^{(i)})^2
J(θ1)=2m1i=1∑m(h(x(i))−y(i))2
至于为何此处方差算法与上文不一致,主要是为了后续的一些计算方便,但对一个方差值求平均并影响其对于当前偏差度的评判,方差本身就只是一个相对值评判,而非绝对值评判。
对J(θ1)J(\theta_1)J(θ1)求导。
dJ(θ1)dθ1=12m∑i=1m(h(x(i))−y(i))×2×dh(x(i))dθ1=1m∑i=1m(h(x(i))−y(i))×d(1+θ1x)dθ1=1m∑i=1m(h(x(i))−y(i))×x(i)=1m∑i=1m(1+θ1x(i)−y(i))×x(i)
\frac{dJ(\theta_1)}{d\theta_1}
= \frac {1}{2m}\sum^{m}_{i=1}(h(x^{(i)}) - y^{(i)}) \times 2 \times \frac{dh(x^{(i)})}{d\theta_1} \\
= \frac {1}{m}\sum^{m}_{i=1}(h(x^{(i)}) - y^{(i)}) \times \frac{d(1+\theta_1x)}{d\theta_1} \\
= \frac {1}{m}\sum^{m}_{i=1}(h(x^{(i)}) - y^{(i)}) \times x^{(i)} \\
= \frac {1}{m}\sum^{m}_{i=1}(1+\theta_1 x^{(i)} - y^{(i)}) \times x^{(i)}
dθ1dJ(θ1)=2m1i=1∑m(h(x(i))−y(i))×2×dθ1dh(x(i))=m1i=1∑m(h(x(i))−y(i))×dθ1d(1+θ1x)=m1i=1∑m(h(x(i))−y(i))×x(i)=m1i=1∑m(1+θ1x(i)−y(i))×x(i)
令去其为0
1m∑i=1m(1+θ1x(i)−y(i))×x(i)=0∑i=1m(x(i))+∑i=1m(θ1(x(i))2)−∑i=1m(y(i)x(i))=0θ1=∑i=1m(y(i)x(i))−∑i=1m(x(i))∑i=1m((x(i))2)
\frac {1}{m}\sum^{m}_{i=1}(1+\theta_1 x^{(i)} - y^{(i)}) \times x^{(i)} =0 \\
\sum^{m}_{i=1}(x^{(i)} ) +\sum^{m}_{i=1}(\theta_1 (x^{(i)})^2) - \sum^{m}_{i=1}( y^{(i)} x^{(i)}) = 0 \\
\theta_1 =\frac{\sum^{m}_{i=1}( y^{(i)} x^{(i)}) -\sum^{m}_{i=1}(x^{(i)} ) }{\sum^{m}_{i=1}( (x^{(i)})^2)}
m1i=1∑m(1+θ1x(i)−y(i))×x(i)=0i=1∑m(x(i))+i=1∑m(θ1(x(i))2)−i=1∑m(y(i)x(i))=0θ1=∑i=1m((x(i))2)∑i=1m(y(i)x(i))−∑i=1m(x(i))
将x,y的数据代入得出θ1\theta_1θ1= 7.0644,与之前步进得出的7.1,非常接近。
%数据的产生,并加入噪声
close all;
x = 0:0.01:1;
y = 4*x.^4+3*x.^3+2*x.^2+x+1+rand(1,length(x));
figure(1);
hold on;
plot(x,y,'r');
%这里设h(x) = 1 + $theta_1 * x, $\theta_1,是我们不确定的,那如何确定呢。
% 先想想,如果不使用算法,你如何确定这两个参数,比较直接的做法
% 是不是先假定这个两个值,如$\theta_1$=3,先看看效果
x = 0:0.01:1;
h = 1*ones(1,length(x))+3*x
c = h-y;
c_var0 = c * c';
plot(x,h,'y');
%效果似乎不太理想,$\theta_1$似乎需要再加大一些,$\theta_1$=4
x = 0:0.01:1;
h = 1*ones(1,length(x))+4*x
c = h-y;
c_var1 = c * c';
plot(x,h,'b');
%效果似乎不太理想,$\theta_1$似乎需要再加大一些,$\theta_1$=5
x = 0:0.01:1;
h = 1*ones(1,length(x))+5*x
c = h-y;
c_var2 = c * c';
plot(x,h,'g');
%效果似乎不太理想,$\theta_1$似乎需要再加大一些,$\theta_1$=8
x = 0:0.01:1;
h = 1*ones(1,length(x))+8*x
c = h-y;
c_var3 = c * c';
plot(x,h,'k');
%这次理想多了
%。但是有没有更好的方法呢,总不能每次数据拟合都不断的人工尝试吧。
%这时候聪明的你肯定会想到,让机器枚举遍历阿,每一次数据拟合都不断的尝试,
%计算最小方差,比如$\theta_1$从0一直到10,每次步进0.1,最终选择方差最小的那个
c_var_min = inf;
theta_best = 0;
for i=1:0.1:10
h = 1*ones(1,length(x))+i*x;
c = h-y;
c_var = c * c';
if(c_var < c_var_min)
c_var_min = c_var;
theta_best = i;
end
plot(x,h,'y');
end
theta_best
h = 1*ones(1,length(x))+theta_best*x;
plot(x,h,'g');
%步进搜索最好theta,并记录方差变化
close all;
c_var_min = inf;
theta_best = 0;
c_var = [];
for i=1:100
h = 1*ones(1,length(x))+i/10*x;
c = h-y;
c_var(i) = c * c';
if(c_var(i) < c_var_min)
c_var_min = c_var(i);
theta_best = i/10;
end
end
n=1:100;
n=n/10;
theta_best
plot(n,c_var,'r');
xlabel("theta_1");
ylabel("var");
hold on;
%解析解求最好theta
theta_1 = (ones(1,length(x))*(x.*y)' - ones(1,length(x))*x')/(ones(1,length(x)) * (x.^2)')
2.2 多个参数
只有一个参数的一阶式,对于原始参数的拟合效果并不好,如果想增强拟合效果,不妨提高假设函数的阶次
设
h(x)=θ0+θ1x+θ2x2+θ3x3+θ4x4
h(x) = \theta_0 + \theta_1 x + \theta_2 x^2 + \theta_3 x^3 + \theta_4x^4
h(x)=θ0+θ1x+θ2x2+θ3x3+θ4x4
因为参数较多,令
Θ=[θ0,θ1,θ2,θ3,θ4]
\Theta = \begin {matrix} [\theta_0 ,\theta_1,\theta_2,\theta_3,\theta_4] \end{matrix}
Θ=[θ0,θ1,θ2,θ3,θ4]
方差函数为,同时我们一般称这类度量函数为代价函数,代价函数还可以是其他类型,不一定用方差
J(Θ)=12m∑i=1m(h(x(i))−y(i))2
J(\Theta)=\frac {1}{2m}\sum^{m}_{i=1}(h(x^{(i)}) - y^{(i)})^2
J(Θ)=2m1i=1∑m(h(x(i))−y(i))2
mmm为数据个数
对于多个参数,可以用2.1中的求导数致0方法,只不过多个参数使用的是偏导。但是呢,求偏导置零求的只是每个θ\thetaθ的局部最优解,而不一定是全局最优解。那么多参数下如何求全局最优解呢。面对这种只有原始数据的多参数拟合问题,无法给出一个如2.1中最后一个式子一样的求全局最优解的解析解。这种时候一般就用搜索迭代的方式。即随便先给Θ\ThetaΘ一个随机初始值,然后不断调整它的值,使得其向总体方差变小的方向改变,最终得到的Θ\ThetaΘ中的每一个值不一定是对应的求偏导并置0后得到的最小值。那如何调整Θ\ThetaΘ的值呢?下面介绍常用的方法
3.梯度下降法
θik=θik−1−α∂J(Θ)∂θi
\theta_i ^k= \theta_i^{k-1} - \alpha\frac {\partial J(\Theta)} {\partial \theta_i}
θik=θik−1−α∂θi∂J(Θ)
α\alphaα为学习率,用于控制梯度下降得快慢
用高中知识理解,求导数的几何意义是求斜率,∂J(Θ)∂θi\frac {\partial J(\Theta)} {\partial \theta_i}∂θi∂J(Θ)>0时说明方差在上升,小于0则说明方差在下降。那么我们调整θi\theta_iθi的值应当向方差减小的方向调整,即∂J(Θ)∂θi\frac {\partial J(\Theta)} {\partial \theta_i}∂θi∂J(Θ)>0,减去它。小于0的时候加上它,最终得到了上述θi\theta_iθi的表达式。
这个式子表示新的θi\theta_iθi等于上一个θi\theta_iθi减去α∂J(Θ)∂θi\alpha\frac {\partial J(\Theta)} {\partial \theta_i}α∂θi∂J(Θ)使得θi\theta_iθi始终朝着使代价函数J(Θ)J(\Theta)J(Θ)下降得方向变化
使用梯度下降法循环100次,或者使J(Θ)J(\Theta)J(Θ)的值下降到可以容许的误差范围内
∂J(Θ)∂θi\frac {\partial J(\Theta)} {\partial \theta_i}∂θi∂J(Θ)的偏导结果
∂J(Θ)∂θ0=1m∑i=1m((h(x(i))−y(i))⋅1)\frac {\partial J(\Theta)} {\partial \theta_0}=\frac {1}{m}\sum^{m}_{i=1}((h(x^{(i)}) - y^{(i)})\cdot 1)∂θ0∂J(Θ)=m1∑i=1m((h(x(i))−y(i))⋅1)
∂J(Θ)∂θ1=1m∑i=1m((h(x(i))−y(i))⋅x)\frac {\partial J(\Theta)} {\partial \theta_1}=\frac {1}{m}\sum^{m}_{i=1}((h(x^{(i)}) - y^{(i)})\cdot x)∂θ1∂J(Θ)=m1∑i=1m((h(x(i))−y(i))⋅x)
∂J(Θ)∂θ2=1m∑i=1m((h(x(i))−y(i))⋅x2)\frac {\partial J(\Theta)} {\partial \theta_2}=\frac {1}{m}\sum^{m}_{i=1}((h(x^{(i)}) - y^{(i)})\cdot x^2)∂θ2∂J(Θ)=m1∑i=1m((h(x(i))−y(i))⋅x2)
∂J(Θ)∂θ3=1m∑i=1m((h(x(i))−y(i))⋅x3)\frac {\partial J(\Theta)} {\partial \theta_3}=\frac {1}{m}\sum^{m}_{i=1}((h(x^{(i)}) - y^{(i)})\cdot x^3)∂θ3∂J(Θ)=m1∑i=1m((h(x(i))−y(i))⋅x3)
∂J(Θ)∂θ4=1m∑i=1m((h(x(i))−y(i))⋅x4)\frac {\partial J(\Theta)} {\partial \theta_4}=\frac {1}{m}\sum^{m}_{i=1}((h(x^{(i)}) - y^{(i)})\cdot x^4)∂θ4∂J(Θ)=m1∑i=1m((h(x(i))−y(i))⋅x4)
代码
%数据的产生,并加入噪声
close all;
x = 0:0.01:1;
y = 4*x.^4+3*x.^3+2*x.^2+x+1+rand(1,length(x));
figure(1);
hold on;
plot(x,y,'r');
%假设函数为h(x) = theata0 + theata1*x+ theata2*x^2 + theata3*x^4
theata = 10*rand(1,5);%随机产生系数
alpha = 1.2;%学习率
for i=1:100%迭代100次
%假设函数
h_theata = theata(1)*ones(1,length(x))+theata(2)*x+theata(3)*x.^2+theata(4)*x.^3+theata(5)*x.^4;
plot(x,h_theata,'y');
var(i) = 1/length(x)*sum((h_theata - y).^2);%方差
%梯度下降法迭代求解新系数,代价函数1/2m *sum((h(x) - y)^2)
theata(1) = theata(1) - alpha*1/length(x)*sum(h_theata - y);
theata(2) = theata(2) - alpha*1/length(x)*sum((h_theata - y).*x);
theata(3) = theata(3) - alpha*1/length(x)*sum((h_theata - y).*x.^2);
theata(4) = theata(4) - alpha*1/length(x)*sum((h_theata - y).*x.^3);
theata(5) = theata(5) - alpha*1/length(x)*sum((h_theata - y).*x.^4);
end
%最终图形
h_theata = theata(1)*ones(1,length(x))+theata(2)*x+theata(3)*x.^2+theata(4)*x.^3+theata(5)*x.^4;
plot(x,h_theata,'b');
title('数据变化');
hold off;
%代价函数1/2m *sum((h(x) - y)^2)的变化曲线
figure(2);
plot(1:100,var);
title('代价函数大小变化');
 图中红线为训练集数据的原始图线,黄色为拟合过程中图线的变化,蓝色为最终拟合曲线。可以看出这种拟合效果相比2.1中强了不少。
图中红线为训练集数据的原始图线,黄色为拟合过程中图线的变化,蓝色为最终拟合曲线。可以看出这种拟合效果相比2.1中强了不少。

在拟合过程中方差或者说代价函数的值的大小变化





















 912
912

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








