HDU 6798 Triangle Collision （二分+几何）

最新推荐文章于 2020-08-25 09:19:33 发布

原创最新推荐文章于 2020-08-25 09:19:33 发布 · 374 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#二分 #计算几何

基础计算几何同时被 2 个专栏收录

16 篇文章

订阅专栏

二分|三分

7 篇文章

订阅专栏

本文介绍了一种使用二分搜索和几何原理解决等边三角形内小球运动轨迹预测的问题，通过复制三角形并计算反射路径，实现了对小球第k次碰撞时刻的精确求解。

题意：边长为L的等边三角形内有一颗小球，给出初始位置和速度，求第k次与边碰撞是在什么时候。

题解：二分+几何
把三角形复制成如下图，点每一次反射我们考虑成是经过了多少条边即可。
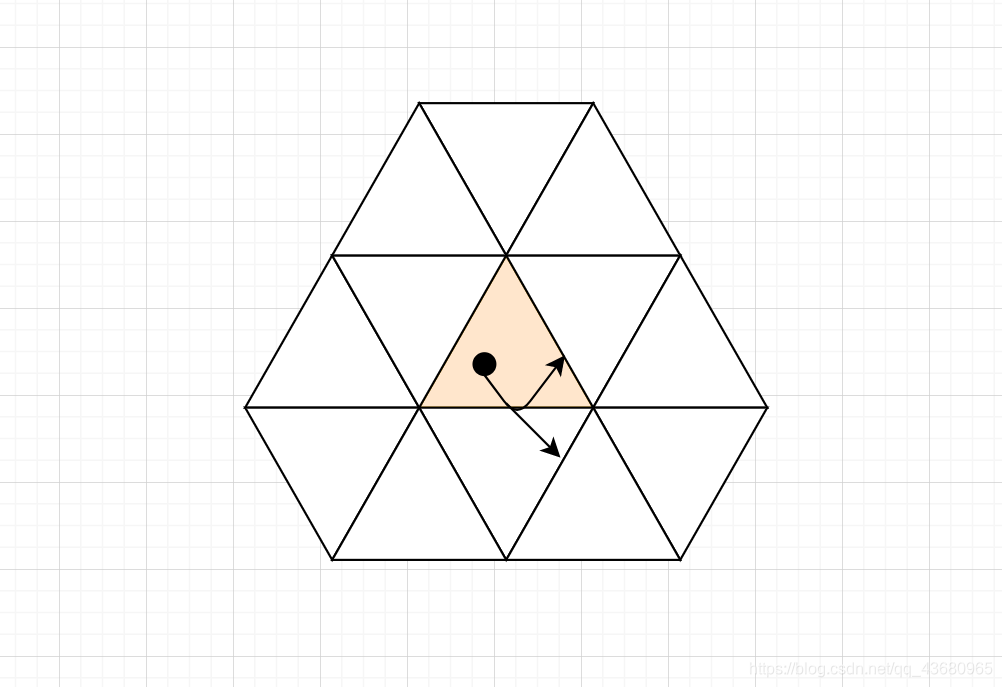
在这里插入图片描述
对于三角形下面一条边，是x轴，可以直接得到。
对于三角形左右的边，我们要进行旋转，即获得以左右两边为x轴时，点的坐标和速度。

eps改1e-6能过。

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<string>
#include<cstring>
#include<algorithm>
#include<queue>
#include<stack>
#include<cmath>
#include<vector>
#include<fstream>
#include<set>
#include<map>
#include<sstream>
#include<iomanip>
#define ll long long
using namespace std;
const double eps = 1e-6;
const double pi = acos(-1.0);
int t;
double l, x, y, vx, vy, k;
double h;
double solve(double y, double vy, double t) {
	return abs(floor((y + vy * t) / h));
}
bool check(double mid) {
	double res = solve(y, vy, mid) +
		solve(fabs((y + sqrt(3) * x - h) / 2), (-sqrt(3) * vx - vy) / 2, mid) +
		solve(fabs((-y + sqrt(3) * x + h) / 2), (vx * sqrt(3) - vy) / 2, mid);
	return res >= k;
}
int main() {
	scanf("%d", &t);
	while (t--) {
		scanf("%lf%lf%lf%lf%lf%lf", &l, &x, &y, &vx, &vy, &k);
        h = l * sqrt(3) / 2;
		double l = 0, r = 1e11, mid;
		while (r - l > eps) {
			mid = (l + r) / 2;
			if (check(mid))
				r = mid;
			else
				l = mid;
		}
        printf("%.8f\n", mid);
	}
	return 0;
}