0绪论
本文主要参考书有:网络科学导论、现代控制理论、线性代数等。
主要解决的是《网络科学导论》一书中第11章网络同步与控制,课后习题11-1。如有证明任何问题欢迎指出并讨论,由于后面有矩阵运算,因此使用katex编辑会出现问题,因此部分公式使用截图。
1问题的提出
节点
i
i
i的初始状态演化方程为:
x
˙
i
(
t
)
=
∑
i
=
1
N
a
i
j
(
x
j
(
t
)
−
x
i
(
t
)
)
{\dot x_i}(t) = \sum\limits_{i = 1}^N {{a_{ij}}({x_j}(t) - {x_i}(t))}
x˙i(t)=i=1∑Naij(xj(t)−xi(t))
其中
i
=
1
,
2
,
3
,
4...
,
N
i = 1,2,3,4...,N
i=1,2,3,4...,N
节点数为
N
N
N个,初始状态为任意给定,网络拓扑固定。证明:
lim
t
→
∞
x
i
(
t
)
=
1
N
∑
j
=
1
N
x
j
(
0
)
\mathop {\lim }\limits_{t \to \infty } {x_i}(t) = {1 \over N}\sum\limits_{j = 1}^N {{x_j}(0)}
t→∞limxi(t)=N1j=1∑Nxj(0)
2问题的解决(两步走)
步骤一:将 x i ( t ) {x_i}(t) xi(t)求转化为求系数% e − L t {e^{ - Lt}} e−Lt的极限:
由《网络科学导论》的366页11-4的结论可得
l
i
j
=
−
a
i
j
(
i
≠
j
)
{l_{ij}} = - {a_{ij}}(i \ne j)
lij=−aij(i=j)
邻接矩阵行和即每个节点的度为:
l
i
i
=
∑
j
=
1
N
a
i
j
=
k
i
{l_{ii}} = \sum\limits_{j = 1}^N {aij} = {k_i}
lii=j=1∑Naij=ki
将节点度改写为对角线矩阵:
D
=
d
i
a
g
(
k
1
,
k
2
,
.
.
.
,
k
N
)
D = diag({k_1},{k_2},...,{k_N})
D=diag(k1,k2,...,kN)
其中矩阵A为邻接矩阵
A
=
(
a
i
j
)
A = ({a_{ij}})
A=(aij)
其中
l
i
j
{l_{ij}}
lij是拉普拉斯矩阵
L
L
L的元素,即可得出
L
=
D
−
A
L = D - A
L=D−A,所以题目中所给演化方程可以改写为关于拉普拉斯矩阵
L
L
L和的函数
x
i
(
t
)
{x_i}(t)
xi(t)(结合实例理解):
X
˙
i
(
t
)
=
−
L
X
i
(
t
)
{\dot X_i}(t) = - L{X_i}(t)
X˙i(t)=−LXi(t)
而后使用一阶微分方程求解的方法:
两边积分
∫
d
X
i
(
t
)
X
i
(
t
)
=
∫
−
L
d
t
\int {{{d{X_i}(t)} \over {{X_i}(t)}}} = \int { - Ldt}
∫Xi(t)dXi(t)=∫−Ldt
得到积分后的等式
ln
(
X
i
(
t
)
)
=
−
L
t
+
C
\ln ({X_i}(t)) = - Lt + C
ln(Xi(t))=−Lt+C
两边取对数
X
i
(
t
)
=
e
−
L
t
∗
X
i
(
0
)
{X_i}(t) = {e^{ - Lt}}*{X_i}(0)
Xi(t)=e−Lt∗Xi(0)
而后问题就转换为求时间趋于无穷的系数极限即可:
lim
t
→
∞
e
−
L
t
=
?
\mathop {\lim }\limits_{t \to \infty } {e^{ - Lt}} = ?
t→∞lime−Lt=?
步骤二:求解系数
e
−
L
t
{e^{ - Lt}}
e−Lt的极限:
为解决这一问题首先在这陈述一下相关应用的定理:凯莱哈密顿定理
介绍凯莱哈密顿定理:
矩阵满足自身的特征方程,若阶矩阵的特征多项式为:
f
(
λ
)
=
[
λ
I
−
B
]
=
λ
n
+
b
n
−
1
λ
n
−
1
+
.
.
.
+
b
1
λ
+
b
0
(公式
1.1
)
f(\lambda ) = [\lambda I - B] = {\lambda ^n} + {b_{n - 1}}{\lambda ^{n - 1}} + ... + {b_1}\lambda + {b_0} (公式1.1)
f(λ)=[λI−B]=λn+bn−1λn−1+...+b1λ+b0(公式1.1)
则有:
f
(
B
)
=
B
n
+
b
n
−
1
B
n
−
1
+
.
.
.
+
b
1
B
+
b
0
I
=
0
(公式
1.2
)
f(B) = {B^n} + {b_{n - 1}}{B^{n - 1}} + ... + {b_1}B + {b_0}I = 0(公式1.2)
f(B)=Bn+bn−1Bn−1+...+b1B+b0I=0(公式1.2)
矩阵指数
e
B
t
{e^{Bt}}
eBt可表示为
B
B
B的
(
n
−
1
)
(n - 1)
(n−1)阶多项式:
e
B
t
=
∑
m
=
0
n
−
1
b
m
(
t
)
B
m
(公式
1.3
)
{e^{Bt}} = \sum\limits_{m = 0}^{n - 1} {{b_m}(t){B^m}} (公式1.3)
eBt=m=0∑n−1bm(t)Bm(公式1.3)
凯莱哈密顿定理所得矩阵
B
B
B满足自己的特征方程,对于上式用
B
B
B的特征值
λ
i
,
i
=
1
,
2
,
.
.
.
,
n
{\lambda _i},i = 1,2,...,n
λi,i=1,2,...,n代替
B
B
B后仍然满足:
e
λ
i
t
=
∑
j
=
0
n
−
1
b
j
(
t
)
λ
i
j
(公式
1.4
)
{e^{{\lambda _i}t}} = \sum\limits_{j = 0}^{n - 1} {{b_j}(t){\lambda _i}^j}(公式1.4)
eλit=j=0∑n−1bj(t)λij(公式1.4)
利用该式可求得待定系数
a
j
(
t
)
{a_j}(t)
aj(t)
所得的
n
n
n元一次方程组为:公式1.5
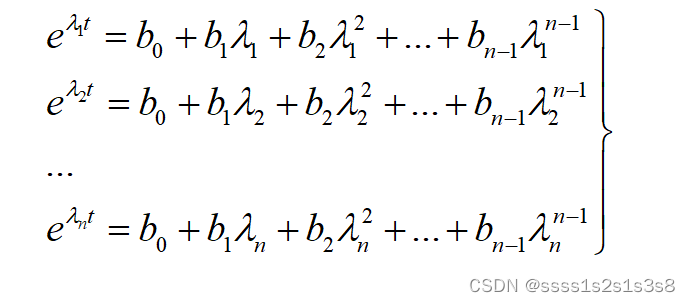
这里插入一个定理:有关实对称阵的性质:
任何一个实对称矩阵都可以正交对角化,即存在一个正交矩阵
S
S
S(
S
T
=
S
−
1
{S^T} = {S^{ - 1}}
ST=S−1)使得
S
−
1
B
S
=
S
T
B
S
=
Λ
{S^{ - 1}}BS = {S^T}BS = \Lambda
S−1BS=STBS=Λ且正交矩阵
S
S
S的列向量不相关、可单位化。
正式求解:
由上述现代控制理论中求状态转移矩阵使用的凯莱哈密顿定理公式(1.5)可得:
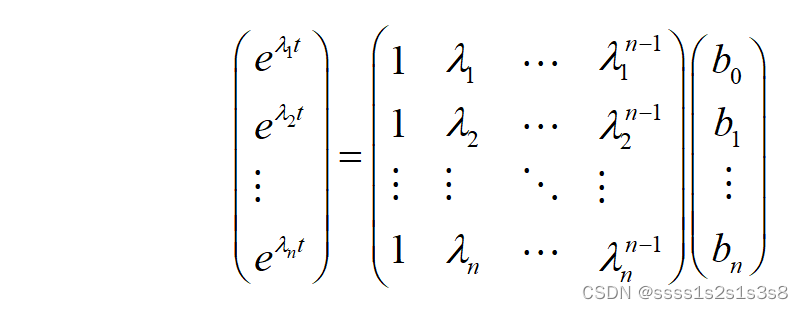
由于系数矩阵行列式必不为0因此可逆,所以两边左乘系数矩阵的逆矩阵得:
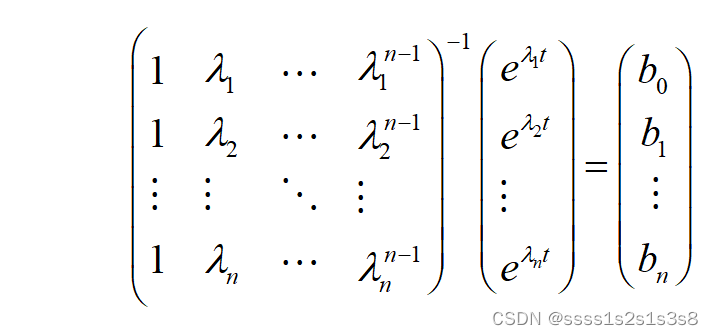
再由公式(1.3)可得下述公式:
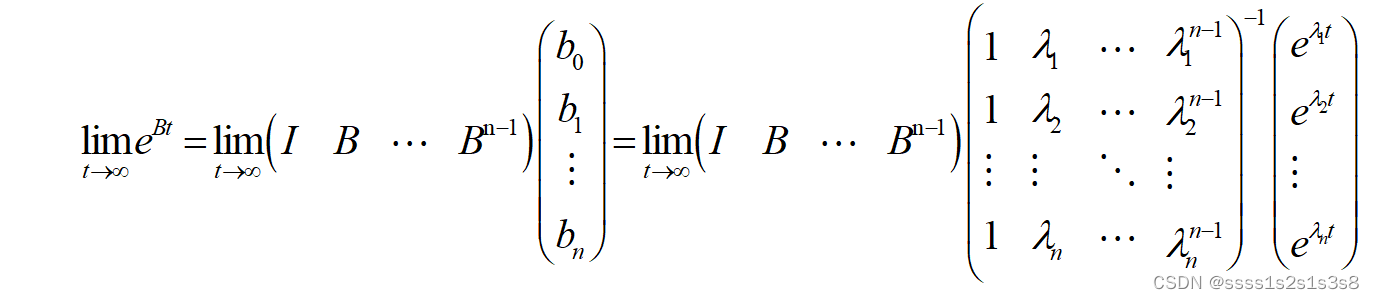
由于
B
=
−
L
B = - L
B=−L矩阵的特征值分别为
−
λ
1
=
0
,
−
λ
2
,
−
λ
3
,
.
.
.
,
−
λ
n
<
0
- {\lambda _1} = 0, - {\lambda _2}, - {\lambda _3},..., - {\lambda _n} < 0
−λ1=0,−λ2,−λ3,...,−λn<0因此极限:
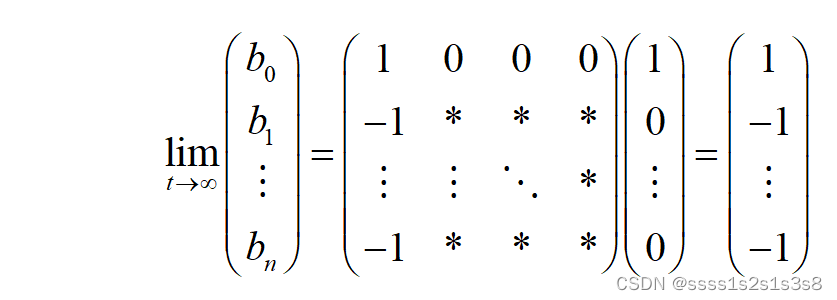
即
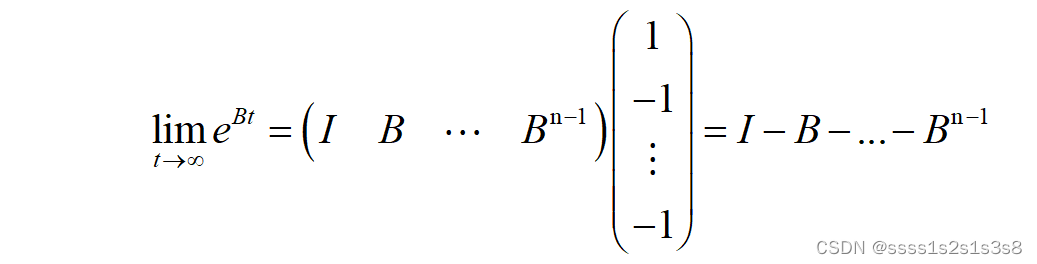
因此设矩阵
−
L
=
B
- L = B
−L=B转换为求
lim
t
→
∞
e
B
t
=
?
\mathop {\lim }\limits_{t \to \infty } {e^{Bt}} = ?
t→∞limeBt=?由矩阵B为实对称阵可将B矩阵转化为:
B
=
S
Λ
S
T
B = S\Lambda {S^T}
B=SΛST
矩阵S为正交矩阵
S
S
T
=
I
S{S^T} = I
SST=I
将原极限转化为下式:
lim
t
→
∞
e
B
t
=
I
−
B
−
.
.
.
−
B
n
−
1
=
S
(
I
−
Λ
−
Λ
2
−
.
.
−
Λ
n
−
1
)
S
T
\mathop {\lim }\limits_{t \to \infty } {e^{Bt}} = I - B - ... - {B^{{\rm{n}} - 1}} = S(I - \Lambda - {\Lambda ^2} - .. - {\Lambda ^{n - 1}}){S^T}
t→∞limeBt=I−B−...−Bn−1=S(I−Λ−Λ2−..−Λn−1)ST
矩阵S为矩阵B的特征向量,因此第一列为
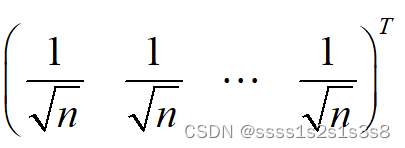
题中所求转换为:
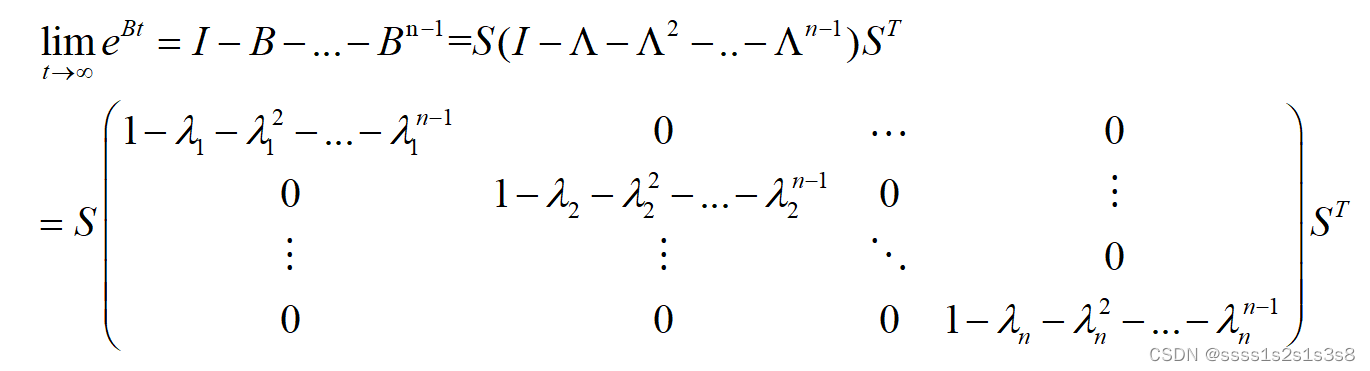
其中:
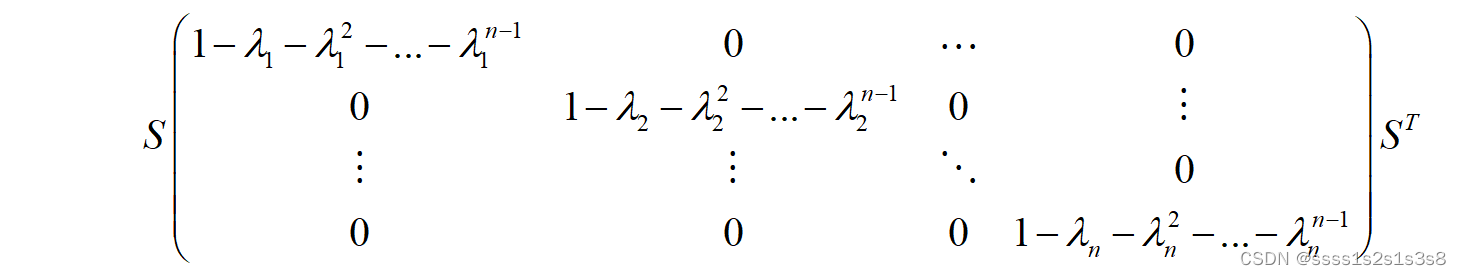
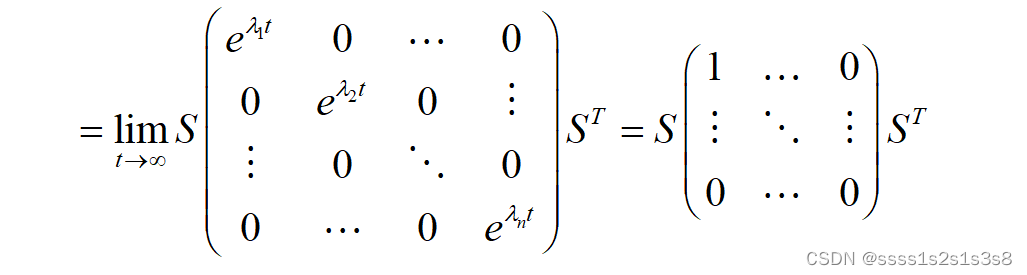
其中:矩阵S为
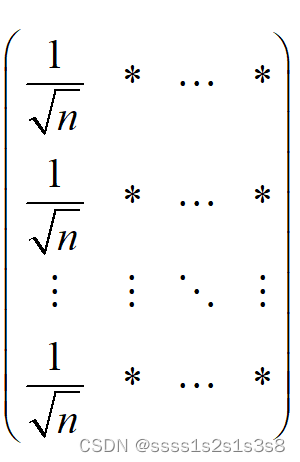
将S带入上述矩阵乘法可得:
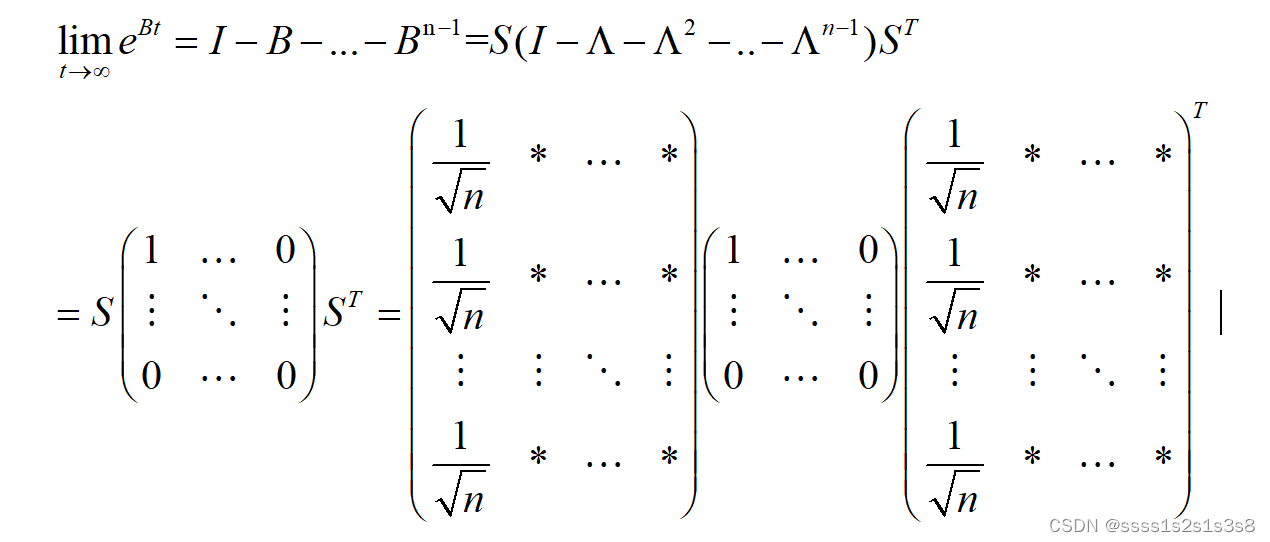
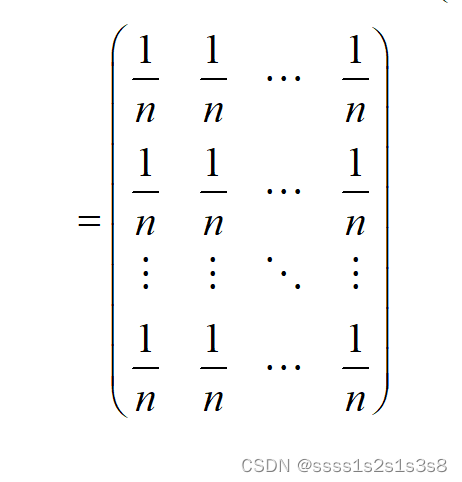
将求得的系数矩阵带入步骤一中的最后结果可得:
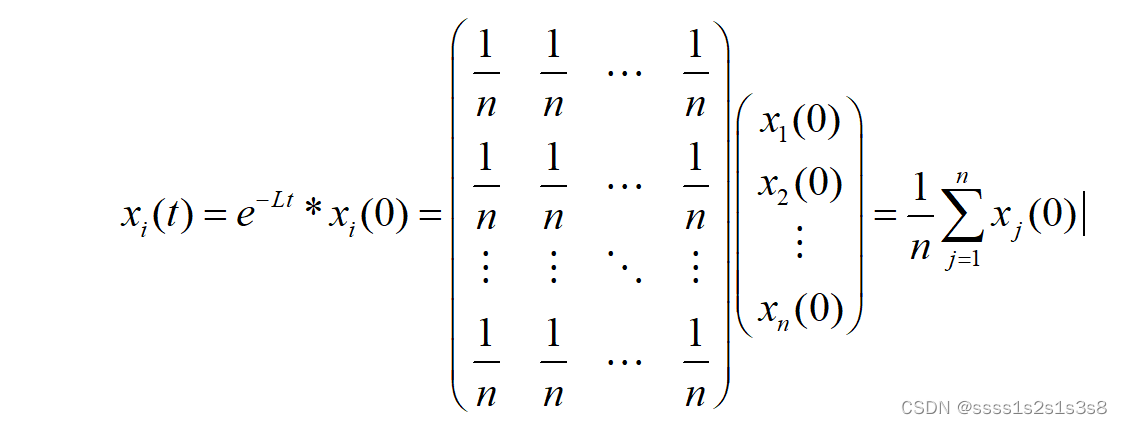
命题得证
3结语
本篇博客仅为记录网络科学中有关网络同步的一个习题解法,网络科学导论一书中的课后习题没有明确给出解答,如有任何问题或者证明步骤有错,请指出交流。






















 3853
3853











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








