数据结构—二叉树算法题总结

最新推荐文章于 2023-04-04 15:26:47 发布

星星leslie

最新推荐文章于 2023-04-04 15:26:47 发布

阅读量1.2k

点赞数 1

分类专栏：算法题记录

本文链接：https://blog.csdn.net/qq_43710486/article/details/102624802

版权

算法题记录专栏收录该内容

20 篇文章 0 订阅

订阅专栏

文章目录

创建和递归遍历(扩展先序遍历序列创建二叉链表)

题目描述

从键盘接收扩展先序序列，以二叉链表作为存储结构，建立二叉树。输出这棵二叉树的先序、中序和后序遍历序列。
二叉树结点的data是字符类型数据, 其中#表示空格字符。

#include <stdio.h>
#include "stdlib.h"
//二叉链表结点结构
typedef struct Node {
    char data;
    struct Node *Lchild;
    struct Node *Rchild;
}BiTNode, *BiTree;
//用一级指针来创建
/*BiTNode *CreateBiTree(BiTree root) {
    char ch;
    ch = getchar();
    if (ch == '#') {
        root = NULL;
    } else {
        root = (BiTree)malloc(sizeof(BiTNode));
        root->data = ch;
        printf("1");
        //和与二级指针不同的是
        //一级指针要求有返回值，所以一定要接收
        root->Lchild = CreateBiTree(root->Lchild);
		//有返回值，所以一定要接收
        root->Rchild = CreateBiTree(root->Rchild);
    }
    return root;
}*/
void CreateBiTree(BiTree *root) {
    char ch;
    ch = getchar();
    if (ch == '#') {
        *root = NULL;
    } else {
        *root = (BiTree)malloc(sizeof(BiTNode));
        (*root)->data = ch;
        //以左子树域地址为参数，可使被调用函数中建立的结点指针置于该域中
        CreateBiTree(&((*root)->Lchild));
        //以右子树域地址为参数，可使被调用函数中建立的结点指针置于该域中
        CreateBiTree(&((*root)->Rchild));
    }
}
void PreOrder(BiTree root) {
    //printf("进来了");
    if (root) {
        printf("%c", root->data);
        PreOrder(root->Lchild);
        PreOrder(root->Rchild);
    }
}
void InOrder(BiTree root) {
    if (root) {
        InOrder(root->Lchild);
        printf("%c", root->data);
        InOrder(root->Rchild);
    }
}
void PostOrder(BiTree root) {
    if (root) {
        PostOrder(root->Lchild);
        PostOrder(root->Rchild);
        printf("%c", root->data);
    }
}
int main(int argc, const char * argv[]) {
    BiTree root;
    //root = (BiTree)malloc(sizeof(BiTNode));
    CreateBiTree(&root);
    PreOrder(root);
    printf("\n");
    InOrder(root);
    printf("\n");
    PostOrder(root);
    printf("\n");
    return 0;
}

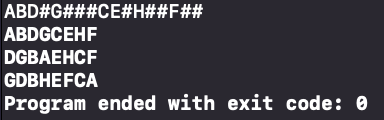
验证结果：
请注意在验证时，一定要输入正确的扩展的先序遍历序列，比如这里的ABD#G###CE#H##F##。随便输一个是不行的，因为它没办法建立起来这棵二叉树
运行结果

创建和非递归遍历(扩展先序遍历序列创建二叉链表)

先序遍历二叉树的非递归实现：
从根开始，当前结点存在或栈非空，重复以下两步
1.访问根节点，根节点入栈，进入根节点左子树，直至为空
2.如果栈不为空，退栈顶结点，进入其右子树。

中序遍历二叉树非递归实现：
从根开始，当前结点存在或栈非空。重复以下两步
1.入栈，进入左子树，直至左子树为空
2.栈不为空，出栈顶元素，访问出栈结点，并进入其右子树

后序遍历二叉树非递归实现:
首先需要一个q指针，一直保持更新指向刚访问的结点
1.入栈，访问其左子树，重复直至左子树为空
2.如栈非空，取栈顶元素，判断他的右子树是否为空或者右子树是否等于q。
如果右子树不为空或等于q，说明没有右子树或者右子树还没有被访问，出栈，访问，更新q = p(q要一直保持更新为刚才访问的结点), p置空(避免再次访问)否则，进入p右子树.


#include <stdio.h>
#include "stdlib.h"
//二叉链表结点结构
typedef struct Node {
    char data;
    struct Node *Lchild;
    struct Node *Rchild;
}BiTNode, *BiTree;
typedef struct Stack {
    BiTNode *stack[100];
    int top;
}SeqStack;
void CreateBiTree(BiTree *root) {
    char ch;
    ch = getchar();
    if (ch == '#') {
        *root = NULL;
    } else {
        *root = (BiTree)malloc(sizeof(BiTNode));
        (*root)->data = ch;
        //以左子树域地址为参数，可使被调用函数中建立的结点指针置于该域中
        CreateBiTree(&((*root)->Lchild));
        //以右子树域地址为参数，可使被调用函数中建立的结点指针置于该域中
        CreateBiTree(&((*root)->Rchild));
    }
}
void init(SeqStack **s) {
    *s = (SeqStack *)malloc(sizeof(SeqStack));
    (*s)->top = -1;
}
int Empty(SeqStack *s) {
    if (s->top == -1) {
        return 0;
    } else {
        return 1;
    }
}
void Push(SeqStack *s ,BiTree pNew) {
    s->top++;
    s->stack[s->top] = pNew;
}
void pop(SeqStack *s, BiTree *p) {
    *p = s->stack[s->top];
    s->top--;
}
void preOrder(BiTree root) {
    SeqStack *s;
    BiTree p;
    init(&s);
    p = root;
    while (p != NULL || Empty(s)) {
        while (p != NULL) {
            printf("%c", p->data);
            Push(s, p);
            p = p->Lchild;
        }
        if (Empty(s)) {
            pop(s, &p);
            p = p->Rchild;
        }
    }
}
void InOrder1(BiTree root) {
    SeqStack *s;
    init(&s);
    BiTree p;
    p = root;
    while (p != NULL || Empty(s)) {
        while (p != NULL) {
            Push(s, p);
            p = p->Lchild;
        }
        if (Empty(s)) {
            pop(s, &p);
            printf("%c", p->data);
            p = p->Rchild;
        }
    }
}
void top(SeqStack *s, BiTree *p) {
    (*p) = s->stack[s->top];
}
void post(BiTree root) {
    SeqStack *s;
    BiTree p, q;
    init(&s);
    p = root;
    q = NULL;
    while (p != NULL || Empty(s)) {
        while (p != NULL) {
            Push(s, p);
            p = p->Lchild;
        }
        if (Empty(s)) {
            top(s, &p);
            if (p->Rchild == NULL || p->Rchild == q) {
                pop(s, &p);
                printf("%c", p->data);
                //q时刻记录刚被访问的结点
                q = p;
                //置空，避免再次被访问
                p = NULL;
            } else {
                p = p->Rchild;
            }
        }
    }
}
int main(int argc, const char * argv[]) {
    BiTree root;
    //root = (BiTree)malloc(sizeof(BiTNode));
    CreateBiTree(&root);
    preOrder(root);
    printf("\n");
    InOrder1(root);
    printf("\n");
    post(root);
    printf("\n");
    return 0;
}

运行结果: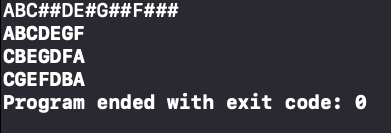 在这里插入图片描述

层次遍历(利用队列)

算法思想:
首先根结点入队，当队列非空时，重复如下两步操作
1.队头结点出队，并访问出队结点
2.出队结点的非空左，右孩子依次入队。



#include <stdio.h>
#include "stdlib.h"
//二叉链表结点结构
typedef struct Node {
    char data;
    struct Node *Lchild;
    struct Node *Rchild;
}BiTNode, *BiTree;
typedef struct Queue {
    BiTNode *Queue[100];
    int front;
    int rear;
}SeqQueue;
void CreateBiTree(BiTree *root) {
    char ch;
    ch = getchar();
    if (ch == '#') {
        *root = NULL;
    } else {
        *root = (BiTree)malloc(sizeof(BiTNode));
        (*root)->data = ch;
        //以左子树域地址为参数，可使被调用函数中建立的结点指针置于该域中
        CreateBiTree(&((*root)->Lchild));
        //以右子树域地址为参数，可使被调用函数中建立的结点指针置于该域中
        CreateBiTree(&((*root)->Rchild));
    }
}
void init(SeqQueue **s) {
    (*s) = (SeqQueue *)malloc(sizeof(SeqQueue));
    (*s)->front = (*s)->rear = -1;
}
void EnterQueue(SeqQueue *s, BiTree root) {
    s->rear++;
    s->Queue[s->rear] = root;
}
int Empty(SeqQueue *s) {
    if (s->front == s->rear) {
        return 0;
    } else {
        return 1;
    }
}
void DeleteQueue(SeqQueue *s, BiTree *p) {
    s->front++;
    *(p) = s->Queue[s->front];
}
void LevelOrder(BiTree root) {
    SeqQueue *s;
    BiTree p;
    init(&s);
    EnterQueue(s, root);
    while (Empty(s)) {
        DeleteQueue(s, &p);
        printf("%c", p->data);
        if (p->Lchild != NULL) {
            EnterQueue(s, p->Lchild);
        }
        if (p->Rchild != NULL) {
            EnterQueue(s, p->Rchild);
        }
    }
}
int main(int argc, const char * argv[]) {
    BiTree root;
    //root = (BiTree)malloc(sizeof(BiTNode));
    CreateBiTree(&root);
    LevelOrder(root);
    printf("\n");
    return 0;
}

运行结果:
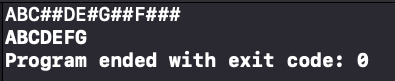
在这里插入图片描述

结点个数

#include <stdio.h>
#include "stdlib.h"
//二叉链表结点结构
typedef struct Node {
    char data;
    struct Node *Lchild;
    struct Node *Rchild;
}BiTNode, *BiTree;
void CreateBiTree(BiTree *root) {
    char ch;
    ch = getchar();
    if (ch == '#') {
        *root = NULL;
    } else {
        *root = (BiTree)malloc(sizeof(BiTNode));
        (*root)->data = ch;
        //以左子树域地址为参数，可使被调用函数中建立的结点指针置于该域中
        CreateBiTree(&((*root)->Lchild));
        //以右子树域地址为参数，可使被调用函数中建立的结点指针置于该域中
        CreateBiTree(&((*root)->Rchild));
    }
}
//定义全局变量
int a = 0, b = 0, c = 0;
void InOrder1(BiTree root) {
    if (root) {
        InOrder1(root->Lchild);
        //度为2的结点
        if ((root->Lchild != NULL && root->Rchild != NULL)) {
            c++;
        }
        //度为1的结点
        if ((root->Lchild == NULL && root->Rchild != NULL) || (root->Lchild != NULL && root->Rchild == NULL)) {
            b++;
        }
        //叶子结点
        if (root->Lchild == NULL && root->Rchild == NULL) {
            a++;
        }
        InOrder1(root->Rchild);
    }
}
//中序输出叶子结点
void InOrder2(BiTree root) {
    if (root) {
        InOrder2(root->Lchild);
        //叶子结点
        if (root->Lchild == NULL && root->Rchild == NULL) {
            printf("%c", root->data);
            a++;
        }
        InOrder2(root->Rchild);
    }
}
int main(int argc, const char * argv[]) {
    BiTree root;
    //root = (BiTree)malloc(sizeof(BiTNode));
    CreateBiTree(&root);
    InOrder1(root);
    printf("%d %d %d\n", a, b, c);
    InOrder2(root);
    return 0;
}

运行结果:
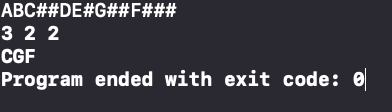
在这里插入图片描述

二叉树的最大深度

方法一：递归

int Max(int a, int b) {
    if (a > b) {
        return a;
    } else {
        return b;
    }
}

int maxDepth(struct TreeNode* root){
    if (root == NULL) {
        return 0;
    }
    int left = maxDepth(root->left);
    int right = maxDepth(root->right);
    return 1 + Max(left, right);
}

方法二：队列（层序遍历）

#define MAX 1000
int maxDepth(struct TreeNode* root) {
    struct TreeNode *list[MAX];
    int count = 0;
    int front, rear;
    front = rear = 0;
    if (root != NULL) {
        list[rear % MAX] = root;
        rear++;
    }
    while (front < rear) {
        count++;
        int j = rear - front;
        for (int i = 0; i < j; i++) {
            struct TreeNode *t;
            t = list[front % MAX];
            front++;
            if (t->left) {
                list[rear % MAX] = t->left;
                rear++;
            }
            if (t->right) {
                list[rear % MAX] = t->right;
                rear++;
            }
        }
    }
    return count;
}

二叉树的最小深度

题目链接
//队列（层次遍历）
总结：相比求最大深度，求最小深度主要是要及时退出循环

#define MAX 1000
int minDepth(struct TreeNode* root){
    struct TreeNode *list[MAX];
    int front, rear;
    front = rear = 0;
    int count = 0;
    if (root) {
        list[rear % MAX] = root;
        rear++;
    }
    while (front < rear) {
        int flag = 0;
        count++;
        int j = rear - front;
        for (int i = 0; i < j; i++) {
            struct TreeNode *t;
            t = list[front % MAX];
            front++;
            if (t->left == NULL && t->right == NULL) {
                flag = 1;
                break;
            } else {
                if (t->left != NULL) {
                    list[rear % MAX] = t->left;
                    rear++;
                } 
                if (t->right != NULL) {
                    list[rear % MAX] = t->right;
                    rear++;
                }
            }
        }
        if (flag == 1) {
            break;
        }
    }
    return count;
}

对称二叉树

题目链接
方法一：递归。
首先判断一个二叉树是否对称是看它的左子树和右子树是否对称，然后左子树和右子树又有相应的左右子树去判断它是否对称。。。依次推导。显然可以用递归解决。

bool isMirror(struct TreeNode *t1, struct TreeNode *t2) {
    //递推终止条件
    //左右子树为空，表示已经遍历结束。
    if (t1 == NULL && t2 == NULL) {
        return true;
    } else if (t1 == NULL || t2 == NULL) {
         //剪支。
        //其中一个为空，显然已经不对称了
        return false;
    } else {
    //否则进一步推导它的左右子树。
    //&&有短路判断。就是说如果t1->val == t2->val为false。则直接return false;
        return ((t1->val == t2->val) && isMirror(t1->left, t2->right) && isMirror(t1->right, t2->left)); 
    }
}
bool isSymmetric(struct TreeNode* root) {
	//传入根结点
    return isMirror(root, root);
}

方法二：迭代
关于递推，迭代，递归的区别详见这篇博客
//使用队列逐层遍历比较

#define MAX 1000
bool isSymmetric(struct TreeNode* root) {
    struct TreeNode *list[MAX];
    int front, rear;
    front = rear = 0;
    list[rear % MAX] = root;
    rear++;
    list[rear % MAX] = root;
    rear++;
    while (front < rear) {
        struct TreeNode *t1;
        t1 = list[front % MAX];
        front++;
        struct TreeNode *t2;
        t2 = list[front % MAX];
        front++;
        if (t1 == NULL && t2 == NULL) {
            //如果两个节点均为空，那么它们
            //肯定没有左子树和右子树了
            //直接进入下一轮循环
            continue;
        } else if (t1 == NULL || t2 == NULL) {
            //其中一个为空，那么肯定不对称了
            //直接返回false;
            return false;
        } else if (t1->val == t2->val) {
            //先判断它们的根节点的val是否相等
            //如果相等，把它们的左子树和右子树入队列
            //注意是交叉入队，因为就是想要比较它们的对称值是否相等
            //画个图就知道了
            list[(rear++) % MAX] = t1->left;
            list[(rear++) % MAX] = t2->right;
            list[(rear++) % MAX] = t1->right;
            list[(rear++) % MAX] = t2->left;
        } else {
            //这里t1->val != t2->val
            //直接false
            return false;
        }
    }
    //如果程序可以走到这里，说明二叉树已经遍历结束
    //并且均符合上面分类讨论的情况
    //返回true
    return true;
}

平衡二叉树

题目链接
这个题是基于求解二叉树的最大深度解决的
这里就是判断他的左右子树的高度差绝对值小于等于1
所以我们可以求得每个左右子树的高度差，然后进行判断。

int Max(int a, int b) {
    if (a > b) {
        return a;
    } else {
        return b;
    }
}

int maxDepth(struct TreeNode* root){
    if (root == NULL) {
        return 0;
    }
    int left = maxDepth(root->left);
    int right = maxDepth(root->right);
    return 1 + Max(left, right);
}
bool isBalanced(struct TreeNode* root){
    if (root == NULL) {
        return true;
    } else {
        int t1 = maxDepth(root->left);
        int t2 = maxDepth(root->right);
        int t = t1 - t2;
        if (abs(t) <= 1) {
            return isBalanced(root->left) && isBalanced(root->right);
        } else {
            return false;
        }
    }
}

翻转二叉树

题目链接
感觉总结二叉树题目是总结递归了
思想:翻转一个二叉树，就是把它的左子树和右子树交换。
然后左子树对应的二叉树又要交换它的左子树和右子树
右子树对应的二叉树又要交换它的左子树和右子树…
以下是我对递归的个人理解：
我感觉递归非常考验一个人的全局意识，
在思考是否要用递归时
你一定不要局限于当前，而应该想它后面的是不是和当前的处理想法是一样的
在实现递归的时候
你又必须要回到当前，想一想当前的代码怎么实现就行。
不要深究后面怎么办
要不然你会觉得这个代码好像又会特别多而很难实现
实际上递归正是帮我们省去了哪些多余代码
交给递归工作栈就行啦

struct TreeNode* invertTree(struct TreeNode* root){
    //递归终止条件
    //如果遍历借宿，返回NULL。
    //开始回溯过程
    if (root == NULL) {
        return NULL;
    }
    //当前我需要二叉树的左子树
    //但是我又希望这个左子树的二叉树它的左子树和二叉树是交换了的
    //所以递归调用
    struct TreeNode *left = invertTree(root->left);
    //同上，当前我需要二叉树的右子树
    //但是我也希望这个右子树的二叉树它的左子树和右子树是交换了的
    //所以递归调用
    struct TreeNode *right = invertTree(root->right);
    //下面两行代码，就是把一个二叉树的左子树和右子树对调
    root->left = right;
    root->right = left;
    //你不用但是你的root是否经过这么
    //多层递归是否还是起点位置
    //因为最后返回的root是经过回溯得到的
    //虽然我们前面不停的root->left
    //root->right
    //但是那是深度搜索的过程
    //最后回溯过程root又回到了起点位置
    return root;
}

依据先序、中序遍历序列创建二叉树

先感谢这位博主的思路
题目思路来源
虽然总结了好几个二叉树的题目，但是每到一个递归新题的时候总是无处下手。
吐槽自己对递归的理解“一看就懂，一写就懵”
拿到这个题自己也想着递归八九不离十了。
拿这个题来说，按照先序根在第一个的特点，递推:不断得把中序拆分。然后逐层返回。最后得出结果。
题目中用到了C库函数中的strchr.用法可以参考我的这篇博客C/C++常用库函数
关于这个题的分析在代码中已详细给出

#include <stdio.h>
#include "stdlib.h"
#include <string.h>
//二叉链表结点结构
typedef struct Node {
    char data;
    struct Node *Lchild;
    struct Node *Rchild;
}BiTNode, *BiTree;
BiTree CreateBiTree(char *pre, char *in, long n) {
//递归终止条件
//只要遇到递归必不可少。
    if (n <= 0) {
        return NULL;
    }
    BiTree root;
    root = (BiTree)malloc(sizeof(BiTNode));
    //先序序列(根左右)中的第一个元素必为树根结点
    root->data = pre[0];
    //计算根结点在中序序列中出现的位置
    //“拆分”中序序列
    char *p = strchr(in, pre[0]);
    //“拆分”中序序列后得到左子树的长度
    //为了下面的递归(自己调用自己)做准备.
    long len = p - in;
    //printf("%ld\n", len);
    //递归求左子树
    //参数一：先序序列(拆分后得到的左子树)，
    //参数二：中序序列(拆分后得到的左子树)
    //参数三：长度
    root->Lchild = CreateBiTree(pre + 1, in, len);
    //递归求右子树
    //同理
    root->Rchild = CreateBiTree(pre + len + 1, p + 1, n - len - 1);
    return root;
}
void postOrder(BiTree root) {
    if (root) {
        postOrder(root->Lchild);
        postOrder(root->Rchild);
        printf("%c", root->data);
    }
}
int main(int argc, const char * argv[]) {
    char preStr[100], inStr[100];
    BiTree root;
    scanf("%s", preStr);
    scanf("%s", inStr);
    root = CreateBiTree(preStr, inStr, strlen(preStr));
    postOrder(root);
    printf("\n");
    return 0;
}

依据中序、后序遍历序列创建二叉树

由上题可以很容易得到此题。


#include <stdio.h>
#include "stdlib.h"
#include <string.h>
//二叉链表结点结构
typedef struct Node {
    char data;
    struct Node *Lchild;
    struct Node *Rchild;
}BiTNode, *BiTree;
BiTree CreateBiTree(char *in, char *post, long n) {
    if (n <= 0) {
        return NULL;
    }
    BiTree root;
    root = (BiTree)malloc(sizeof(BiTNode));
    root->data = post[n - 1];
    char *p;
    p = strchr(in, post[n - 1]);
    long len = p - in;
    //printf("%ld\n", len);
    root->Lchild = CreateBiTree(in, post, len);
    root->Rchild = CreateBiTree(in + len + 1, post + len, n - len - 1);
    return root;
}
void preOrder(BiTree root) {
    if (root) {
        printf("%c", root->data);
        preOrder(root->Lchild);
        preOrder(root->Rchild);
    }
}
int main(int argc, const char * argv[]) {
    char inStr[100], postStr[100];
    BiTree root;
    scanf("%s", inStr);
    scanf("%s", postStr);
    root = CreateBiTree(inStr, postStr, strlen(inStr));
    preOrder(root);
    printf("\n");
    return 0;
}

结点及其所在层次

题目描述

从键盘接收扩展先序序列，以二叉链表作为存储结构，建立二叉树。按先序遍历次序输出各结点的内容及相应的层次数，要求以二元组的形式输出，其所对应的输出结果为：（data,level）
data是二叉树结点数据域值，level是该结点所在的层次。
设根节点在第一层。
输出的元素间不用间隔，（）都是英文字符

样例输入 Copy

AB#DG###CE##FH###
样例输出 Copy

(A,1)(B,2)(D,3)(G,4)(C,2)(E,3)(F,3)(H,4)

void PreOrder(BiTree root, int level) {
    if (root) {
        printf("(%c,%d)", root->data, level);
        PreOrder(root->Lchild, level + 1);
        PreOrder(root->Rchild, level + 1);
    }
}

int main(int argc, const char * argv[]) {
    BiTree root;
    //root = (BiTree)malloc(sizeof(BiTNode));
    CreateBiTree(&root);
    int level = 1;
    PreOrder(root, level);
    printf("\n");
    return 0;
}

某层叶子结点个数

题目描述

从键盘接收扩展先序序列，以二叉链表作为存储结构，建立二叉树。并计算指定的第K层的叶子结点个数。设根结点在第一层。
第一行：扩展先序序列
第二行：k的值
样例输入 Copy

ABC##DE#G##F###
3

样例输出 Copy

int k, num = 0;
void PreOrder(BiTree root, int level) {
    //printf("进来了");
    if (root) {
        if (level == k && root->Lchild == NULL && root->Rchild == NULL) {
            num++;
        }
        //printf("(%c,%d)", root->data, level);
        PreOrder(root->Lchild, level + 1);
        PreOrder(root->Rchild, level + 1);
    }
}
int main(int argc, const char * argv[]) {
    BiTree root;
    //root = (BiTree)malloc(sizeof(BiTNode));
    CreateBiTree(&root);
    int level = 1;
    scanf("%d", &k);
    PreOrder(root, level);
    printf("%d", num);
    printf("\n");
    return 0;
}

哈夫曼

题目描述

假设某通信报文的字符集由A,B,C,D,E,F这6个字符组成，它们在报文中出现的频度（频度均为整数值）。
(1)构造一棵哈弗曼树，依次给出各字符编码结果。
(2)给字符串进行编码。
(3)给编码串进行译码。

规定：
构建哈弗曼树时：左子树根结点权值小于等于右子树根结点权值。
生成编码时：左分支标0，右分支标1。

输入

第一行：依次输入6个整数，依次代表A,B,C,D,E,F的频度，用空格隔开。
第二行：待编码的字符串
第三行：待译码的编码串
输出

前6行依次输出各个字符及其对应编码，格式为【字符:编码】（冒号均为英文符号）
第7行：编码串
第8行：译码串
样例输入 Copy

3 4 10 8 6 5
BEE
0010000100111101
样例输出 Copy

A:000
B:001
C:10
D:01
E:111
F:110
001111111
BADBED


#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define N 30
#define M 2 * N - 1
typedef struct {
    int index;
    int weight;
    int Parent, Lchild, Rchild;
}HTNode, HuffmanTree[M + 1];
typedef struct {
    HTNode data[1000];
    int top;
}SeqStack;
typedef char * Huffmancode[100];
void init(SeqStack **s) {
    (*s) = (SeqStack *)malloc(sizeof(SeqStack));
    (*s)->top = -1;
}
void push(SeqStack *s, HTNode x) {
    s->top++;
    s->data[s->top] = x;
}
void pop(SeqStack *s, int *p) {
    (*p) = s->data[s->top].index;
    s->top--;
}
void pop2(SeqStack *s) {
    //(*p) = s->data[s->top];
    s->top--;
}
int top1(SeqStack *s) {
    return s->data[s->top].weight;
}
int top2(SeqStack *s) {
    return s->data[s->top - 1].weight;
}
void twoMinSelect(HTNode ht[], int n, int *s1, int *s2) {
    SeqStack *s;
    init(&s);
    HTNode q, p;
    q.weight = 999;
    p.weight = 999;
    push(s, q);
    push(s, p);
    for (int i = 1; i <= n; i++) {
        if (ht[i].Parent == 0) {
            if (ht[i].weight <= top1(s) && top1(s) >= top2(s)) {
                pop2(s);
                push(s, ht[i]);
            } else if (ht[i].weight <= top1(s) && top1(s) <= top2(s)){
                push(s, ht[i]);
            } else if (ht[i].weight < top1(s) || ht[i].weight < top2(s)) {
                push(s, ht[i]);
            }
        }
    }
    if (top1(s) > top2(s)) {
        pop(s, s2);
        pop(s, s1);
    } else {
        pop(s, s1);
        pop(s, s2);
    }
}

//建立哈夫曼树
void CrtHuffmanTree(HuffmanTree ht, int w[], int n) {
    int m = 2 * n - 1;
    for (int i = 1; i <= n; i++) {
        ht[i].index = i;
        ht[i].weight = w[i];
        ht[i].Parent = 0;
        ht[i].Lchild = 0;
        ht[i].Rchild = 0;
    }
    for (int i = n + 1; i <= m; i++) {
        ht[i].index = i;
        ht[i].weight = 0;
        ht[i].Parent = 0;
        ht[i].Lchild = 0;
        ht[i].Rchild = 0;
    }
    for (int i = n + 1; i <= m; i++) {
        int s1, s2;
        twoMinSelect(ht, i - 1, &s1, &s2);
        ht[i].weight = ht[s1].weight + ht[s2].weight;
        ht[i].Lchild = s1;
        ht[i].Rchild = s2;
        ht[s1].Parent = i;
        ht[s2].Parent = i;
    }
}
//哈夫曼编码
void CrtHuffmanCode1(HuffmanTree ht, Huffmancode hc, int n) {
    char *cd;
    int start;
    cd = (char *)malloc(n * sizeof(char));
    cd[n - 1] = '\0';
    for (int i = 1; i <= n; i++) {
        start = n - 1;
        int c = i;
        int p = ht[i].Parent;
        while (p != 0) {
            --start;
            if (ht[p].Lchild == c) {
                cd[start] = '0';
            } else {
                cd[start] = '1';
            }
            c = p;
            p = ht[p].Parent;
        }
        hc[i] = (char *)malloc((n - start) * sizeof(char));
        strcpy(hc[i], &cd[start]);
    }
    free(cd);
}
//译码
void Output(Huffmancode hc) {
    char ch = 65;
    for (int i = 1; i <= 6; i++) {
        printf("%c:%s\n", ch, hc[i]);
//        if (i != 6) {
//            printf("\n");
//        }
        ch++;
    }
}
void secondQuestion(char will[], Huffmancode hc) {
    int lenth = 0;
    int j = 0;
    while (will[j]) {
        lenth++;
        j++;
    }
    for (int i = 0; i < lenth; i++) {
        for (int j = 65; j <= 71; j++) {
            if (will[i] == j) {
                printf("%s", hc[j - 64]);
            }
        }
    }
}
//16 5 10 20 3 1
//ABC
//11000110010
void thirdQuestion(HuffmanTree ht, char *third) {
//    for (int i = 1; i <= 11; i++) {
//        printf("%d:%d %d %d %d\n", i, ht[i].weight, ht[i].Parent, ht[i].Lchild, ht[i].Rchild);
//    }
    int length = 0;
    int j = 0;
    while (third[j]) {
        length++;
        j++;
    }
    //printf("length:%d\n", length);
    int t = 11;
    int k = 0;
    for (int i = 0; i < length; i = k) {
        while (1) {
            if (ht[t].Lchild == 0 && ht[t].Rchild == 0) {
            //下标t与字母之间是有关系的，t-1+'A'即对应字符的ASCII码
                printf("%c", t - 1 + 'A');
                t = 11;
                break;
            } else {
                if (third[k] == '1') {
                    t = ht[t].Rchild;
                    k++;
                } else {
                    t = ht[t].Lchild;
                    k++;
                }
            }
        }
    }
}
int main(int argc, const char * argv[]) {
    int w[100] = {0};
    for (int i = 1; i <= 6; i++) {
        scanf("%d", &w[i]);
    }
    char will[50];
    char third[50];
    scanf("%s", will);
    scanf("%s", third);
    HuffmanTree ht;
    Huffmancode hc;
    CrtHuffmanTree(ht, w, 6);
    CrtHuffmanCode1(ht, hc, 6);
    Output(hc);
    secondQuestion(will, hc);
    printf("\n");
    thirdQuestion(ht, third);
    printf("\n");
    return 0;
}

星星leslie

关注

1
点赞
踩
13

收藏

觉得还不错? 一键收藏
0
评论
数据结构—二叉树算法题总结

文章目录二叉树的最大深度二叉树的最小深度二叉树的最大深度方法一：递归int Max(int a, int b) { if (a > b) { return a; } else { return b; }}int maxDepth(struct TreeNode* root){ if (root == NULL) {...
复制链接

扫一扫