二手车交易价格预测--特征工程

TASK 3 特征工程
如果说上一次的EDA只是对数据的一个全面感受和理解，那么这次的特征工程就是要抽丝剥茧、找到数据和预测值之间的关系，从而为建立模型打下坚实的基础。在这次的特征工程中，我们从更深层次的角度来“清洗”数据，经过数据预处理、特征提取与构造、特征筛选这几个步骤进一步加深对数据分析的理解。

数据预处理

数据预处理通常有一下几种方法

1. 异常值处理：处理方式主要包括箱线图、3σ准则或利用模型进行离群点检测等；
2. 缺失值处理：处理方式主要包括删除（缺失值过多）、插值补全、不处理等；
3. 特征变换：归一化/标准化可以去除量级对数据的影响，使各个特征都在统一水平上。标准化可以转化为标准正态分布、归一化可以转换到[0, 1]区间。

在这次处理过程中，我们首先进行异常值的删除，下面是大佬包装的一个异常处理代码

def outliers_proc(data, col_name, scale=3):	
	def box_plot_outliers(data_ser, box_scale):
		iqr = box_scale * (data_ser.quantile(0.75) - data_ser.quantile(0.25))
	        val_low = data_ser.quantile(0.25) - iqr
	        val_up = data_ser.quantile(0.75) + iqr
	        rule_low = (data_ser < val_low)
	        rule_up = (data_ser > val_up)
	        return (rule_low, rule_up), (val_low, val_up)
 
    data_n = data.copy()
    data_series = data_n[col_name]
    rule, value = box_plot_outliers(data_series, box_scale=scale)
    index = np.arange(data_series.shape[0])[rule[0] | rule[1]]
    print("Delete number is: {}".format(len(index)))
    data_n = data_n.drop(index)
    data_n.reset_index(drop=True, inplace=True)
    print("Now column number is: {}".format(data_n.shape[0]))
    index_low = np.arange(data_series.shape[0])[rule[0]]
    outliers = data_series.iloc[index_low]
    print("Description of data less than the lower bound is:")
    print(pd.Series(outliers).describe())
    index_up = np.arange(data_series.shape[0])[rule[1]]
    outliers = data_series.iloc[index_up]
    print("Description of data larger than the upper bound is:")
    print(pd.Series(outliers).describe())
    fig, ax = plt.subplots(1, 2, figsize=(10, 7))
    sns.boxplot(y=data[col_name], data=data, palette="Set1", ax=ax[0])
    sns.boxplot(y=data_n[col_name], data=data_n, palette="Set1", ax=ax[1])
    return data_n

在删除异常数据的时候，我们就要区分开Train_data和Test_data数据了，Train_data的数据是可以删除的，而Test_data则不能删除，那接下来我们就尝试调用一下这个清洗数据的函数吧！

Train_data = outliers_proc(Train_data, 'power', scale=3)

特征构造

1. 目标：从现有数据特征中构造提取具有区分度或强相关度的特征，辅助提升模型精度；
2. 构建统计特征：包括均值、求和、比例、标准差、计数等；
3. 时间特征：包括相对时间、绝对时间、节假日、双休日等；
4. 地理信息：包括分箱、分布编码；
5. 非线性变换：包括log/平方/根号。

首先我们将训练集和测试集放在一起，方便构造特征，首先使用时间：data[‘creatDate’] - data[‘regDate’]，反应汽车使用时间，一般来说价格与使用时间成反比；接着从邮编中提取城市信息，相当于加入了先验知识；还可以计算某品牌的销售统计量，注意这里以Train的数据计算统计量。
接下来就是数据分桶了，做数据分桶的原因：

1. 离散后稀疏向量内积乘法运算速度更快，计算结果也方便存储，容易扩展；
2. 离散后的特征对异常值更具鲁棒性，如 age>30 为 1 否则为 0，对于年龄为 200 的也不会对模型造成很大的干扰；
3. LR 属于广义线性模型，表达能力有限，经过离散化后，每个变量有单独的权重，这相当于引入了非线性，能够提升模型的表达能力，加大拟合；
4. 离散后特征可以进行特征交叉，提升表达能力，由 M+N 个变量编程 M*N 个变量，进一步引入非线形，提升了表达能力；
5. 特征离散后模型更稳定，如用户年龄区间，不会因为用户年龄长了一岁就变化。

我们以 power 为例

bin = [i*10 for i in range(31)]
data['power_bin'] = pd.cut(data['power'], bin, labels=False)
data[['power_bin', 'power']].head()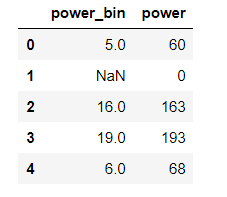

这时数据可以给树模型使用了，可以导出csv文件，接着继续构造特征给其他模型使用，我们对每个特征都做归一化，这里提出一个问题等后续填坑：应该如何从图中看出数据有没有做过分桶或者正常不正常呢？总之，在特征做归一化过程中，发现power呈长尾分布，所以我们应该做长尾分布截断，接着取其log变换再进行归一化；此时来到最后一步，对类别特征进行 OneEncoder。

特征筛选

这里也有几种方法

1. 过滤式
2. 包裹式
3. 嵌入式

这里只写一下过滤式，过滤式也分了几种实现方法：Relief、方差选择、相关系数、卡方检验、互信息法 ，这里我们用相关系数，主要就是对特征进行相关性分析(和Task2很像)，当然看图是非常直观的，再从中进行选择，这里注意选择过程与后续的学习器无关哦。

今天的学习就到这里啦，期待Task4的教学~