算法题之青蛙过河的两种解法思路

青蛙过河

一只青蛙想要过河。 假定河流被等分为若干个单元格，并且在每一个单元格内都有可能放有一块石子（也有可能没有）。 青蛙可以跳上石子，但是不可以跳入水中。

给你石子的位置列表 stones（用单元格序号 升序 表示）， 请判定青蛙能否成功过河（即能否在最后一步跳至最后一块石子上）。开始时， 青蛙默认已站在第一块石子上，并可以假定它第一步只能跳跃 1 个单位（即只能从单元格 1 跳至单元格 2 ）。

如果青蛙上一步跳跃了 k 个单位，那么它接下来的跳跃距离只能选择为 k - 1、k 或 k + 1 个单位。 另请注意，青蛙只能向前方（终点的方向）跳跃。

示例 1：

输入：stones = [0,1,3,5,6,8,12,17]
输出：true
解释：青蛙可以成功过河，按照如下方案跳跃：跳 1 个单位到第 2 块石子, 然后跳 2 个单位到第 3 块石子, 接着 跳 2 个单位到第 4 块石子, 然后跳 3 个单位到第 6 块石子, 跳 4 个单位到第 7 块石子, 最后，跳 5 个单位到第 8 个石子（即最后一块石子）。

示例 2：

输入：stones = [0,1,2,3,4,8,9,11]
输出：false
解释：这是因为第 5 和第 6 个石子之间的间距太大，没有可选的方案供青蛙跳跃过去。

提示：

2 <= stones.length <= 2000
0 <= stones[i] <= 231 - 1
stones[0] == 0
stones 按严格升序排列

要注意的点：

1. 由示例一可看出并不是所有石头都必须要跳，可以选择跳过这个石头。
2. 另外每次跳跃的距离只能是上次跳跃距离的-1或+1或不变。

备注：本人并不专门研究算法，所以不会去尽力优化运行占用的内存或是运行时间。只是喜欢思考点小逻辑，固若有此需求请自行优化。

思路：计算机对比人类极大的优势便是擅长穷举判断。这题中我看到有两个需要每次执行去判断的点。可以理解为两种思路。

1. 遍历下一个石块到底要不要跳，判断是否有跳的条件。
2. 遍历下一步的步数是+1-1还是0，判断这一步能不能跳到石头上。

思路1：遍历下一个石块到底要不要跳，判断是否有跳的条件。

	class Cs1{
        public static boolean enter(int[] stones) {
            return judgment(stones,0,0);
        }
        /**
         * @param stones: 石头数组
         * @param index: 当前位置索引
         * @param jumping: 上次跳跃距离
         */
        private static boolean judgment(int[] stones,int index,int jumping) {
            //若索引达到石块长度，则返回true
            if(index==stones.length-1)
                return true;
            //下一石块到此石块距离
            int distance=stones[index+1]-stones[index];
            //若下一石块到此石块距离>jumping+1则之后所有石块都跳不过去直接返回false
            if (distance>jumping+1)
                return false;
            //若下一石块到此石块距离<jumping-1则跳过下一石块
            else if (distance<jumping-1){
                return (nextJudgment(stones,index,jumping));
            //下一石块可以跳跃
            }else {
                //此时我们可以选择跳到下一石块或者跳过下一石块，优先测试跳到下一石块
                //之后的石头也可跳则返回true
                if(judgment(stones,index+1,distance)){
                    System.out.println("distance:"+distance);
                    return true;
                }
                //再测试跳过下一石块
                return (nextJudgment(stones,index,jumping));
            }
        }
        //跳过下一节点的情况
        private static boolean nextJudgment(int[] stones,int index,int jumping) {
            //如果下一石块已经是最后一块则返回false
            if (index+2==stones.length)
                return false;
            //构建删除stones下标为index+1的数组
            int[] newStones=deleteIndex(stones,index+1);
            return (judgment(newStones,index,jumping));
        }
        //删除stones中索引为index的元素
        private static int[] deleteIndex(int[] stones,int index){
            int[] newStones=new int[stones.length-1];
            int j=0;
            for(int i=0;i<stones.length;i++ ){
                if( i != index )
                    newStones[j++] = stones[i];
            }
            return newStones;
        }

    }

验证：

public static void main(String[] args) {
        int[] stones= {0,1,3,5,6,8,12,13,17};//0,1,3,5,6,8,12,17//0,1,2,3,4,8,9,11//0,1,3,5,6,8,12,13,17//0,1,2,3,4,5,6,7,8,9,10,15,20
        System.out.println(Cs1.enter(stones));
    }

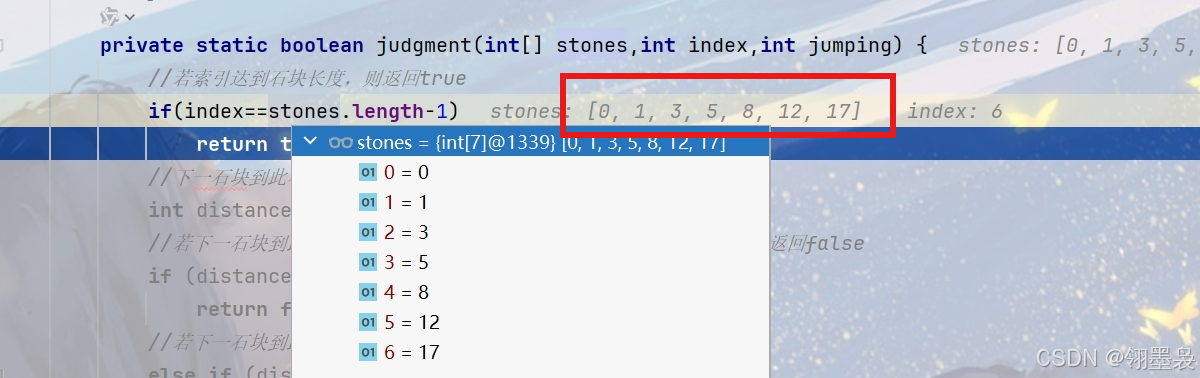
打上断点查看实际可跳路径

数组1.（原题示例数组1）0,1,3,5,6,8,12,17
可走路径：

每次跳的步数：（递归，从下往上看）

数组2.（原题示例数组2）0,1,3,5,6,8,12,17
结果：

数组3.【0,1,3,5,6,8,12,13,17】比起示例1多了个13石头
可走路径：

每次跳的步数：

数组4.【0,1,2,3,4,5,6,7,8,9,10,15,20】
可走路径：

每次跳的步数：

思路2：遍历下一步的步数是+1-1还是0，判断这一步能不能跳到石头上。

class Cs2{
        public static boolean enter(int[] stones) {
            return judgment(stones,0,0);
        }
        /**
         * @param stones: 石头数组
         * @param index: 当前位置索引
         * @param jumping: 上次跳跃距离
         */
        private static boolean judgment(int[] stones,int index,int jumping) {
            //若索引达到石块长度，则返回true
            if(index==stones.length-1)
                return true;
            //分别对应选择距离-1，距离不变，距离+1的可能性
            for (int i=-1;i<2;i++){
                //新石头位置的索引
                int sy=retIndex(stones,index,jumping+i);
                //能跳到石头上且下一步也能跳到石头上则返回true
                if (sy!=-1&&judgment(stones,sy,jumping+i)){
                    System.out.println("走的石头的索引:"+sy);
                    return true;
                }
            }
            return false;
        }

        //返回能跳到的石头所在位置的索引,跳不到石头上则返回索引-1
        private static int retIndex(int[] stones,int index,int jumping) {
            //下一石头数值=当前位置石头数值+跳跃距离
            int newStoneText=stones[index]+jumping;
            for (int ind=index+1;ind<stones.length;ind++){
                if (stones[ind]==newStoneText)
                    return ind;
            }
            return -1;
        }

    }

测试数组0,1,2,3,4,5,6,7,8,9,10,15,20
结果：

测试数组0,1,3,5,6,8,12,17
结果：

测试数组0,1,2,3,4,8,9,11
结果：

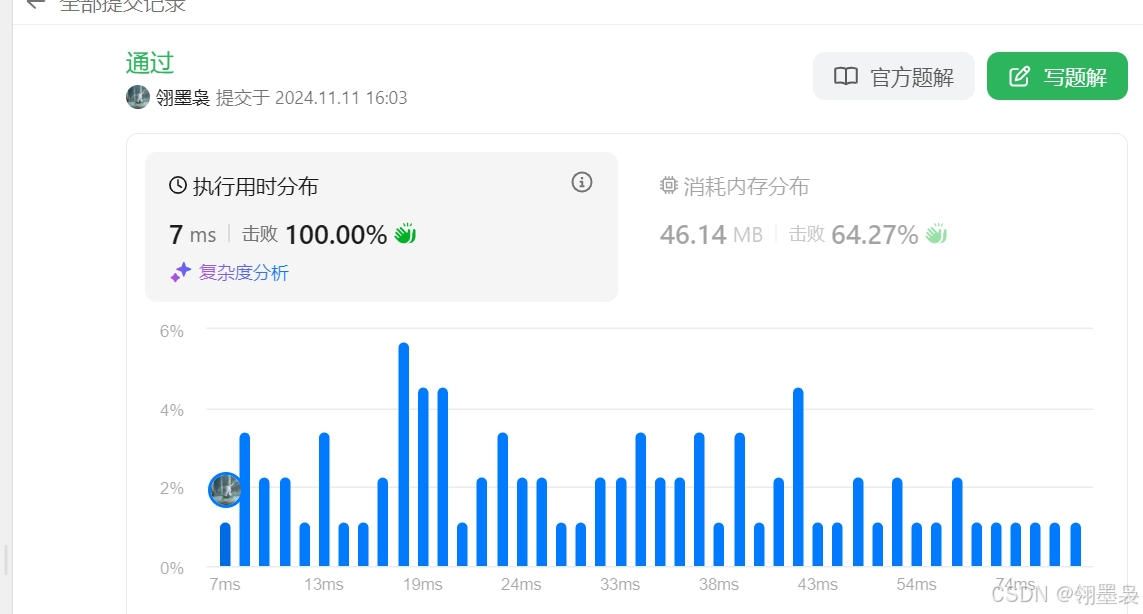
思路2优化速度，添加二维数组保存计算过不可行的数据。对已经计算过不可行的数据不在重复计算

class Solution {
    //0：当前位置索引，1上次跳跃距离（如果判断过不可行则进行记录）
    boolean hc[][];
    public boolean canCross(int[] stones) {
        int len = stones.length;
        hc = new boolean[len][len];
        return judgment(stones,0,0);
    }

    /**
     * @param stones: 石头数组
     * @param index: 当前位置索引
     * @param jumping: 上次跳跃距离
     */
    private boolean judgment(int[] stones,int index,int jumping) {
        //若索引达到石块长度，则返回true
        if(index==stones.length-1)
            return true;
        //有过计算不可行记录
        if (hc[index][jumping])
            return false;
        //分别对应选择距离-1，距离不变，距离+1的可能性
        for (int i=-1;i<2;i++){
            //新石头位置的索引
            int sy= Arrays.binarySearch(stones,index+1,stones.length,stones[index]+jumping+i);
            //能跳到石头上且下一步也能跳到石头上则返回true
            if (sy>=0&&judgment(stones,sy,jumping+i)){
                return true;
            }
            else hc[index][jumping]=true;
        }
        return false;
    }
}