ch-6.2 非线性最小二乘

问题描述：

 这里自变量x 属于Rn，f 是任意一个非线性函数，我们设它有m 维：f(x)属于Rm。

现有两种解法：

1、解析法：令目标函数的导数为零，然后求解x 的最优值，就和一个求二元函数的极值一样，但是fx的形式复杂，不一定能求出解析解。

2、数值法：对于不方便直接求解的最小二乘问题，我们可以用迭代的方式，从一个初始值出发，不断地更新当前的优化变量，使目标函数下降。具体步骤可列写如下：

数值法问题问题关键在于Δxk的求解，求解增量Δxk的最直观方式就是将目标函数在x附件进行泰勒展开：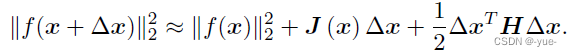

 这里J 是∥f(x)∥2 关于x 的导数（雅可比矩阵），而H 则是二阶导数（海塞（Hessian）矩阵）

现就Δxk的求解给出几种算法。

---

一阶梯度法（梯度下降）

如果保留一阶梯度，那么增量的方向为：

 手推：

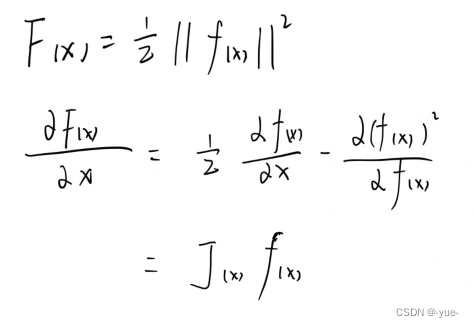
这里的梯度是目标函数的梯度，导数（梯度）是增量的方向，梯度取反就是梯度下降的方向，通常不会直接让J代表步长，会加因子或者饱和函数。

---

二阶梯度法（牛顿法）

如果保留二阶梯度信息，那么增量方程为：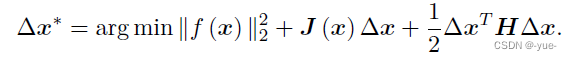

 这个式子在Fx的基础上计算最合适的Δx，使得F(x+Δx)达到最小；x在式中是一个参数，真正的变量是Δx，当x确定下来后，Δx也就直接确定下来；如果能求出Δx的解析解，那么在任意位置x都能准确知道Δx，使得F(x+Δx)达到最小。

手推：

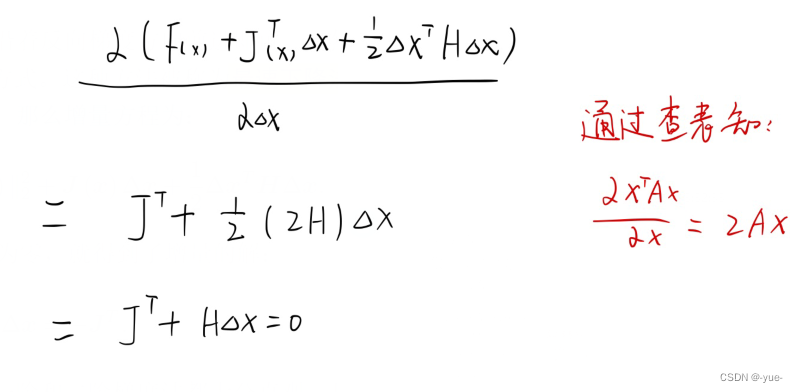
 缺点：梯度下降法过于贪心，容易走出锯齿形路线；牛顿法中，海森矩阵H计算不易，求逆也不易。

---

改进二阶-高斯牛顿法

Gauss Newton的思想是将f(x) 进行一阶的泰勒展开（请注意不是目标函数f(x)2），优点是使用一阶展开的平方产生二阶项，从而避免求Fx的海森矩阵。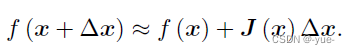

 这里J(x) 为f(x) 关于x 的导数，实际上是一个m×n 的矩阵，也是一个雅可比矩阵。根据前面的框架，当前的目标是为了寻找下降矢量Δx，使得∥f (x + Δx)∥2 达到最小。为了求Δx，我们需要解一个线性的最小二乘问题：

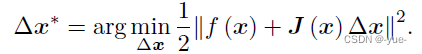
 手推：

 

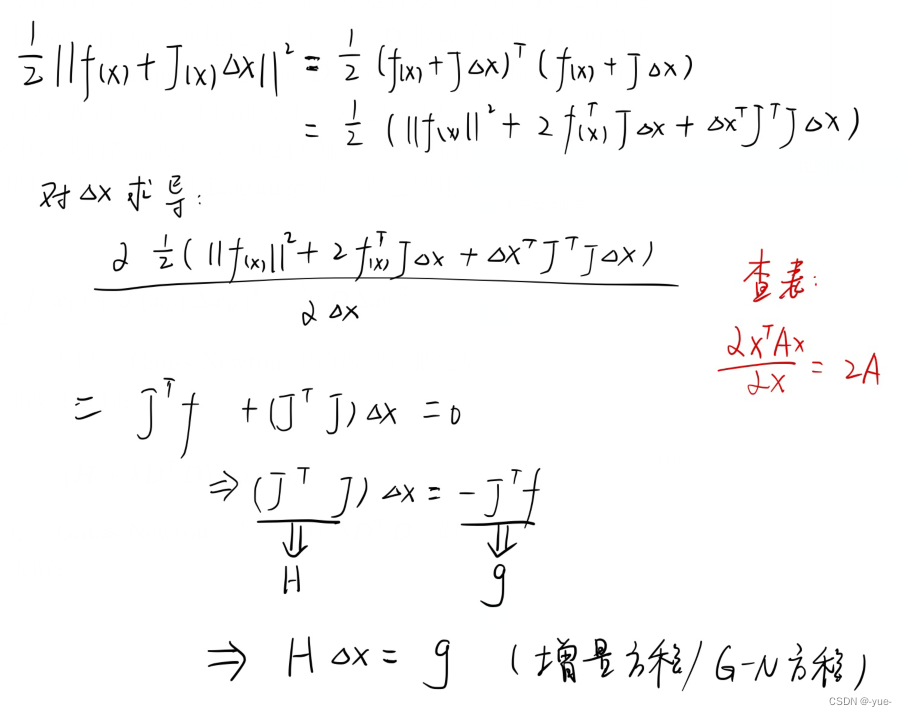
求解增量方程是整个优化问题的核心所在。如果我们能够顺利解出该方程，那么Gauss-Newton 的算法步骤可以写成：

 缺点：JJ'是半正定的，不一定可逆，这会导致迭代增量稳定性变差，算法不收敛；步长Δx的尺度无法很好的把握，容易造成不收敛。

---

Levenberg-Marquadt列文伯格-马夸尔特

 高斯牛顿法中用JJ'代替海森矩阵，只在展开点附件有较好的近似效果，此方法为Δx设定一个信赖区域，在信赖区域里边，我们认为近似是有效的；出了这个区域，近似可能会出问题。

考虑使用可信度指标来判断泰勒近似是否够好。ρ的分子是实际函数下降的值，分母是近似模型下降的值。

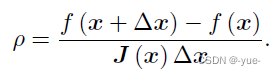
如果ρ太小，说明实际减小的值远少于近似减小的值，则认为近似比较差，需要缩小近似范围。反之，如果ρ 比较大，则说明实际下降的比预计的更大，我们可以放大近似范围。

L-M流程：

 对于上述流程2中如何求解带不等式约束的最小二乘问题，G-N方法求方向吗，改变迭代步长；L-M方法是在给定信任域下同时确定长度和方向。我们用Lagrange 乘子（拉格朗日）将它转化为一个无约束优化问题：

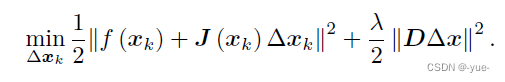
这里入为Lagrange 乘子，D 取成非负数对角阵，D表示信任域的形状，单位阵表示球形域。

手推：

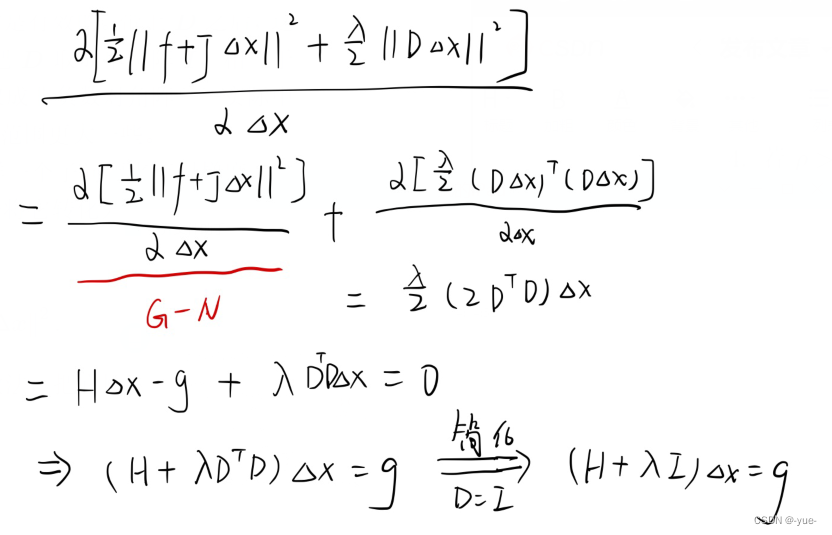
当参数入比较小时，H 占主要地位，这说明二次近似模型在该范围内是比较好的，L-M 方法更接近于G-N 法。另一方面，当入 比较大时，入I 占据主要地位，L-M更接近于一阶梯度下降法（即最速下降），这说明附近的二次近似不够好。L-M 的求解方式，可在一定程度上避免线性方程组的系数矩阵的非奇异和病态问题，提供更稳定更准确的增量Δx。

L-M方法可以看成梯度下降和高斯牛顿之间的融合，通过入来切换两种方法。