【深度学习（deep learning）】花书第9章 卷积网络 读书笔记

【深度学习（deep learning）】花书第9章 卷积网络 读书笔记

---

前言

打基础，阅读花书，感觉一次性啃不动。看一点算一点，写一点笔记留作纪念。以便日后查看与回顾。大名鼎鼎CNN。 2020.11.27-2020.11.29

---

以下是正式内容。

一、卷积

1.1 卷积运算

一般意义上，卷积是对两个实变函数的一种数学运算。
用*表示：
$$s\left(t\right)=\left(x\ast w\right)\left(t\right)$$

以实数为自变量的函数就是实变函数。

例1：时刻t，对应时刻的位置x(t)，加权函数w(a),测量结果距当前时刻的时间间隔a，得到对于位置的平滑估计函数：
$$s\left(t\right)=\int x\left(a\right)w\left(t-a\right)da$$
上式就是卷积运算。

形式上，与概率论里提到的卷积公式是完全一致的。
第一个参数（x）是输入
第二个参数（w) 是核函数
输出有时被称为特征映射（feature map）

例2：卷积公式：X+Y=Z，则：$$f_{X+Y}\left(z\right)={\int }_{-\infty }^{\infty }{f}_X\left(z-y\right)f_Y\left(y\right)dy$$
离散形式的卷积：$$s\left(t\right)=\left(x\ast w\right)\left(t\right)=\sum _{a=-\infty }^{\infty }x\left(a\right)w\left(t-a\right)$$
应用中：

输入的是多维数组（张量）
核是关于张量的参数
输入是有限的点集，将有限个数的求和代替无限的求和

多维度的卷积：（二维）
$$s\left(i,j\right)=\left(I\ast K\right)\left(i,j\right)=\sum _m\sum _{n}I\left(m,n\right)K\left(i-m,j-n\right)$$卷积是可交换的（对核相对输入进行了翻转）：$$s\left(i,j\right)=\left(K\ast I\right)\left(i,j\right)=\sum _m\sum _{n}I\left(i-m,j-n\right)K\left(m,n\right)$$卷积的互相关函数（卷积的一种形式）$$s\left(i,j\right)=\left(I\ast K\right)\left(i,j\right)=\sum _m\sum _{n}I\left(i+m,j+n\right)K\left(m,n\right)$$
二维的卷积（图来自花书）：矩阵对应元素相乘再求和的过程。

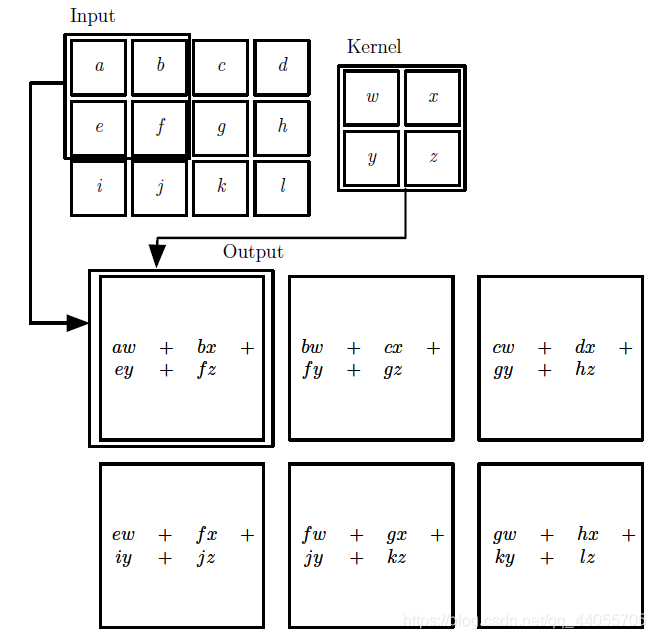
1.2 卷积的动机

利用卷积运算替代矩阵乘法计算

1.2.1 稀疏交互（sparse interactions）

也叫做稀疏连接，稀疏权重
一般，输入m会通过权重矩阵，与每一个输出n都有交互（关系/连接）。每一个输出都需要将所有输入计算一遍，复杂度是m * n。
卷积运算限制了感受野，每个输入最多只会和卷积核大小相同数目的输出有关系。每个输出只与其卷积范围k内的输入做运算，复杂度是 k * n，而k一般远小于m。
通过层间的感受野叠加，深层的输出是和底层的绝大部分输入是间接交互的。

1.2.2 参数共享（parameter sharing）

一般，每个输入与每个输出都有一个对应的权重，这些参数只在计算这一特定交互时有用，总共要有m*n个参数。
而卷积中，对应卷积核同一位置关系的输入输出组共用一个参数，存储和维护的参数数目降到了k个。

1.2.3 等变表示（equivariant representations）

卷积使网络层具有对平移等变的性质。
等变：输入改变，输出也以同样的方式发生改变。
平移等变：图片平移过后，再进行卷积 与 卷积后将结果平移，对于一张进行平移变换的图片是等效的。
也就是说，卷积其实只和输入元素与其相邻元素有关系，与元素的绝对位置无关。只要元素的相对位置不发生变化，那么卷积的结果就不变。但是如果使用权重矩阵的话，元素的绝对位置发生变化，其系数就会发生变化，结果也就不相同。

1.3 深度学习中的卷积

1.3.1 并行卷积

使用多个卷积核，提取出多种特征。

1.3.2 卷积通道

输入值不仅仅是实数值，也可能是一个向量。那么输入由2维矩阵变成了3维张量。向量中的每个分量，对应了传统的一层输入矩阵，对应每个分量都有一个卷积核，称为不同的通道。
只有输入和输出的通道数目相同时，多通道的卷积才是可交换的。
形式化表达：
输入V（i，j，k）第i个通道，第j行，第k列的元素
卷积核K（i，j，k，l）输出是第i个通道，输入在第j个通道，输入与输出有k行l列的偏置
则输出Z：
$${\mathbf{Z}}_{i,j,k}=\sum _{l,m,n}{\mathbf{V}}_{l,j+m-1,k+n-1}{\mathbf{K}}_{i,l,m,n}$$即各个通道上的分量再求和得到最后结果（单通道）。
图示：（图来自参考文献4 https://github.com/MingchaoZhu/DeepLearning）

1.3.3 步长

减少卷积运算的次数（丢失一些特征，减低特征提取的精度），减少计算开销。
每个s个像素进行一个采样，看作对全卷积函数的一个下采样。（在矩阵V的行列索引更新中加一个s系数，每更新一次，加一个s）s称为下采样卷积的步幅。
步长变化，会影响输出的尺寸。

1.3.4 填充（padding）

每卷积一次，输出的尺寸会缩小一次，缩小约卷积核尺寸的大小（实际是卷积核尺寸-1）。
输出的尺寸减少，意味着下一层输入的尺寸就减少，卷积核的大小也要跟着变化，不变化的话，网络会快速的收缩。进行0填充，可以使输入尺寸与卷积核大小分开控制。

1. 有效卷积：完全不使用填充，且只卷积到卷积核右侧边框抵达输入右侧边框。越卷积图片越小，会快速收缩，且限制了网络的深度。
2. 相同卷积：每次填充到输入与输出有相同的大小。网络层数可以任意了。但是边界像素对输出的影响相对中间像素会弱化。
3. 全卷积：进行大量0填充，使得每个像素都被卷积了k次。

好的填充程度应该在相同到有效之间。

1.3.5 非共享卷积

一般的卷积情况下：参与卷积运算的输入与输出之间，存在一个权重，且带权重的连接都是局部的，稀疏的，相对位置一样的输入与输出之间的权重还一样。
非共享卷积：保持这种局部连接关系，但是相对位置的输入输出间的权重不再完全一致。可以看作卷积每行进一步，换一个卷积核。
图示（图来自花书）：

1.3.6 平铺卷积

介于局部连接和全卷积之间。
相邻位置的卷积核不一样，但是又具有一定周期性（以卷积核的集合的大小为周期）。
图示：（图来自花书）

1.4 高效的卷积算法

1. 卷积等效于使用傅里叶变换将输入与核转换到频域/执行两个信号的逐点相乘，再使用傅里叶逆变换转换回时域。有时候利用这一属性比单纯的离散卷积计算更快。
2. 可分离卷积
   图来自参考文献4.
   

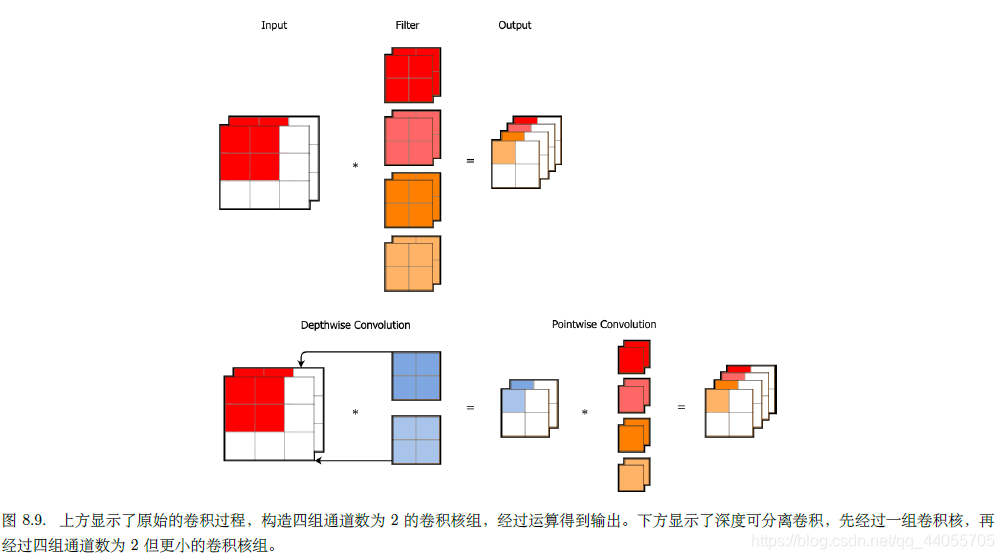
二、池化

原本网络中一个单元，先进行仿射变换，然后利用激活函数进行非线性变换。
利用卷积操作之后，先进行卷积，然后激活。现在，在激活后再加入一个池化函数。
池化函数：使用某一位置的相邻输出的总体统计特征来替代网络在该位置的输出。

• 最大池化函数：相邻矩形区域的最大值。
• 平均池化函数：平均值。
• L2范数
• 距中心像素距离的加权平均。

局部平移不变性：不论什么池化函数，在输入做少量平移时，池化能够帮助输入的表示 近似不变，大部分输出并不改变。（当少量平移时，池化函数操作范围内的输入会有少量的变化，大部分保持不变，那么总体的统计特征也会有稍微的影响，总是总体上还会保持。）
学习不变性：如果在卷积层面，使用不同的参数使得学到不同的特征（对应不同的变化），使用最大池化可以封装这些不同的计算通道，表现为对于这些变化总能够识别出来（做出相同的输出）。

池化可以有效地用于降低输出维数，统一分类层的输入维数

三、卷积神经网络 CNN

适用于网格结构的数据，时序数据可以看作一维网格，图像数据也看作二维的像素网格。
卷积和池化可以看作对于参数的一个无限强的先验。
卷积网络具有处理可变尺寸输入的能力。

3.1 卷积的学习与训练

要实现卷积网络的学习与训练，必须能够完成卷积核的梯度的计算。也就是说，对卷积运算的两个参数要能够求导。

3.1.1 卷积的向量/矩阵表示

卷积是一种线性运算，对应元素相乘后再求和，非常类比于向量的内积运算，因此可以考虑使用矩阵乘法（一次卷积即为向量内积）来表示卷积运算。

直观地，将输入张量压缩成一个一维向量。
定义一个权值矩阵用于运算，矩阵是关于卷积核的一个函数，具有稀疏性，卷积核的元素重复性地复制给这个矩阵。
再将这个权值矩阵与输入向量相乘得到卷积的结果（输出向量）。

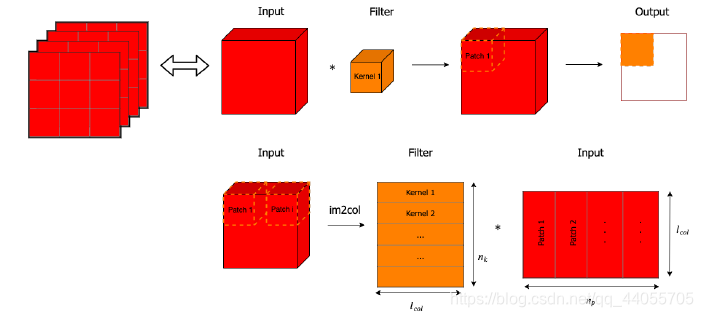
将卷积视为，核块与数据块的内积，那么整个运算可以写成： 核块展开向量组 * 数据块展开向量组。
数据块展开向量组与原始的输入数据矩阵有一定的差别。
一个块的展开成向量的过程：

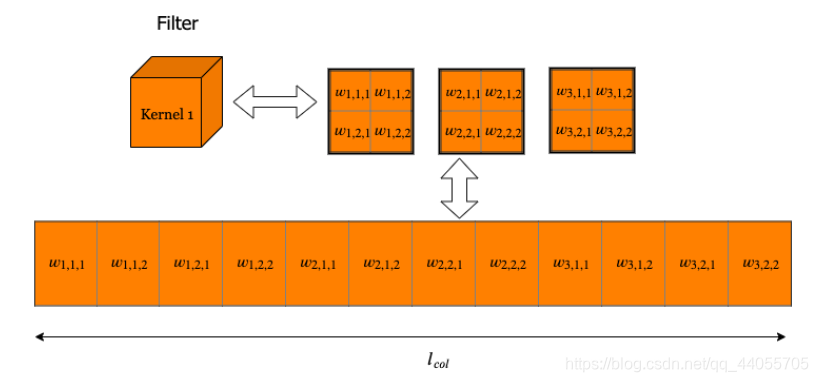
上面两图都来自参考文献四（https://github.com/MingchaoZhu/DeepLearning）

3.1.2 卷积的反向传播

对于图像V，卷积核K，假设有卷积c（带有步长），得到输出K：

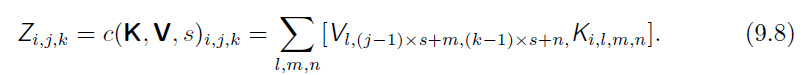
得到一个张量G，为损失函数对输出的导数：$${\mathbf{G}}_{i,j,k}=\frac{\partial }{\partial {\mathbf{Z}}_{i,j,k}}J\left(\mathbf{V},\mathbf{K}\right)$$
为了训练网络，要对核中权重求导，使用函数g
$$g{\left(\mathbf{G},\mathbf{V},s\right)}_{i,j,k,l}=\frac{\partial }{\partial {\mathbf{K}}_{i,j,k,l}}J\left(\mathbf{V},\mathbf{K}\right)=\sum _{m,n}{\mathbf{G}}_{i,m,n}{\mathbf{V}}_{j,\left(m-1\right)\times s+k,\left(n-1\right)\times s+l}$$
如果还有前一层，则需要对输入求导，使用函数h

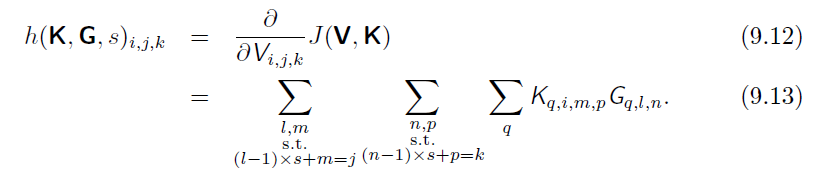
四、典型网络

略。等看完cs231n回来补充。

参考资料

1.机器学习，周志华
2.统计学习方法，第二版，李航
3.https://zhuanlan.zhihu.com/p/38431213
4.https://github.com/MingchaoZhu/DeepLearning
5.https://www.bilibili.com/video/BV1kE4119726?p=5&t=1340
6.cs231n